二维机器学习测试数据生成
最近在看mlapp的第七八章,讲的是线性回归和逻辑回归的内容
当然就难免写点代码来进行实验,总喜欢自己做一些数据而不只是写一个原函数再加上噪声
毕竟自己点点点出来然后得到学习的直线比较有feel,所有就需要这样一个东西:
一个坐标系上点点点出一些点,然后自动生成点的数据放在程序里来跑
估计是东西太小,都没看人做个,纠结一番还是自己动手做了一个
【【【【【【【【地址在此,请用支持html5的浏览器打开】】】】】】】】
我学javascript和html也比较浅,反正各种参考最后是搞出来了
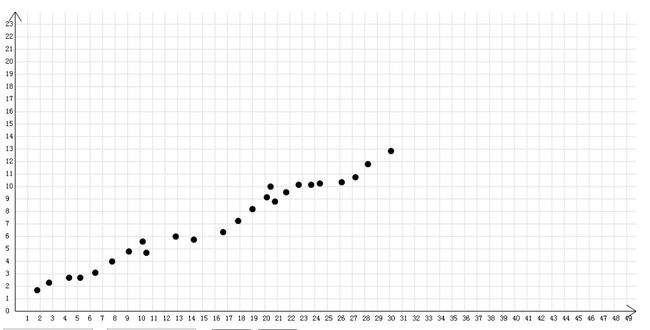
大概的界面就是下面这个样子,可以输入宽和高调节坐标系的大小
(负数就没搞出来了,反正是学习用的)
点生成数据按钮在下面的文本框里得到数据,可以选择是否在每个样例前添加一个常数1(具体啥用知道的都知道)
可以选择regression(X内容是x的坐标,y的内容是点的y轴的坐标值)
或者logistic模式(X的内容是点的完整坐标,y的内容是点的标号)
默认是regression模式的
生成的数据可以直接放在python里面跑,比如:
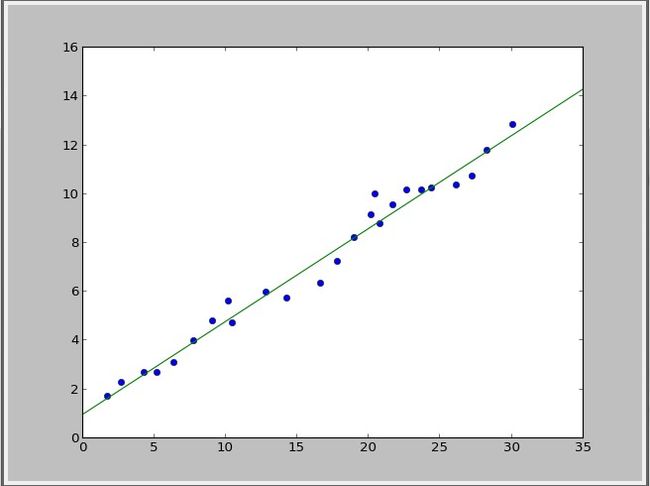
生成的数据放在python里的fit出来的结果就是:(下面的横轴坐标不均匀,所以看起来有点变形,其实没有)
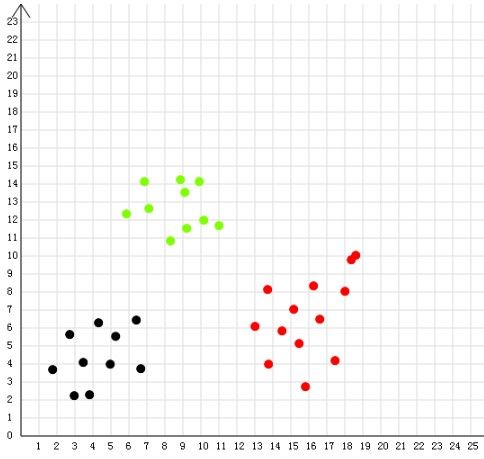
而上图生成的logistic样例就是下面这样,这样就不用苦逼地自己去编数据了,点点几下东西就出来了^_^
X=[ [1,1.7611110925674438,3.6876739501953124], [1,2.7111110925674438,5.637673950195312], [1,4.311111092567444,6.2876739501953125], [1,3.4611110925674438,4.087673950195312], [1,5.261111092567444,5.5376739501953125], [1,6.4111110925674435,6.437673950195313], [1,6.6611110925674435,3.7376739501953127], [1,3.811111092567444,2.2876739501953125], [1,2.9611110925674438,2.2376739501953127], [1,4.961111092567444,3.9876739501953127], [1,5.861111092567444,12.337673950195313], [1,6.861111092567444,14.137673950195312], [1,7.111111092567444,12.637673950195312], [1,8.311111092567444,10.837673950195313], [1,9.211111092567444,11.537673950195312], [1,8.861111092567445,14.237673950195312], [1,9.911111092567443,14.137673950195312], [1,9.111111092567445,13.537673950195312], [1,10.161111092567443,11.987673950195312], [1,11.011111092567443,11.687673950195313], [1,13.011111092567443,6.087673950195312], [1,13.711111092567444,8.137673950195312], [1,15.161111092567443,7.0376739501953125], [1,15.461111092567444,5.137673950195312], [1,15.811111092567444,2.7376739501953127], [1,13.761111092567443,3.9876739501953127], [1,14.511111092567443,5.837673950195312], [1,16.261111092567443,8.337673950195313], [1,16.611111092567445,6.487673950195313], [1,17.461111092567442,4.187673950195313], [1,18.011111092567443,8.037673950195312], [1,18.361111092567445,9.787673950195312], [1,18.611111092567445,10.037673950195312]] y=[ [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [2], [2], [2], [2], [2], [2], [2], [2], [2], [2], [1], [1], [1], [1], [1], [1], [1], [1], [1], [1], [1], [1], [1]]