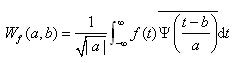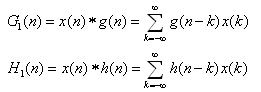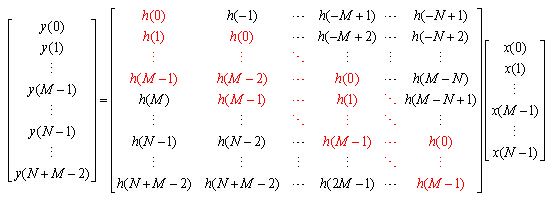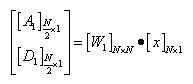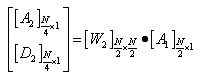压缩感知稀疏基之离散小波变换
题目:压缩感知稀疏基之离散小波变换
看小波变换的时间超过半个月了,到今天为止终于可以得到小波变换矩阵(小波基)了,该陆续写一些总结了,这一篇给出最核心的东西:在Matlab中如何得到小波变换矩阵?
我看小波变换的最终目的也是为了得到小波变换矩阵,因为小波并不是目的,看小波是为了研究压缩感知的稀疏表示。但小波变换真心不是一般的正交变换,它没有一个简单的公式可以表达,里面涉及的概念太多,一时无法吸收消化。
离散小波变换(DiscreteWavelet Transform, DWT)和离散傅里叶变换(Discrete FourierTransform, DFT)不一样,在Matlab中确实有dwt函数,但它与一般书中讲的DWT不一样,dwt是基于Mallat(法国学者,音译为马拉特)算法实现的,针对的离散时间信号,而DWT指的是将连续小波变换(Continuous WaveletTransform, CWT)中的尺度参数a和时移参数b离散化,即将下式中的a和b离散化,但t仍然是连续的。
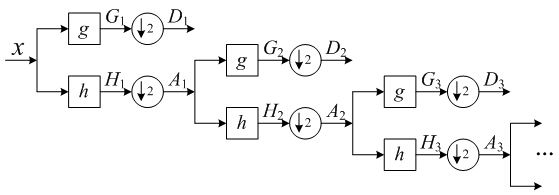
Mallat算法框图如下:
小波变换跟普通的正交变换不同,它是一个多层分解。如Mallat算法框图所示,一个长为N的信号x,第一层分解为高频部分D1和低频部分A1,长度均为N/2;第二层分解将A1分解为高频部分D2和低频部分A2,长度均为N/4;第三层分解将A2分解为高频部分D3和低频部分A3,长度均为N/8,依此类推,但分解所得到的所有结果长度总和仍为N,例如一层分解后得到D1和A1(两个长度为N/2的序列),二层分解后得到D1、D2和A2(N/2+N/4+N/4),三层分解后得到D1、D2、D3和A3(N/2+N/4+N/8+N/8)。
不同的小波母函数对应的小波基不同,在特定小波基下最多可以分解多少层在Matlab中可以使用函数wmaxlev去求解。
在Mallat算法框图中,多层分解的过程相当于滤波的过程,例如由x0分别得到d1和x1相当于让x0分别通过滤波器h1和h0,然后再下采样,每两个点抽取一个点。滤波的过程实际上就是卷积了,但这里就有一个问题:N点长的序列与M点长的序列线性卷积后长度为N+M-1,并不等于N,也就是说下采样后每两点抽取一点得到的结果并不是N/2,而且线性卷积的四个步骤(反转、平移、相乘、相加)在计算卷积结果两侧的点时,反转平移后两个卷积序列只有部分点对应上,到底如何处理边界的这些点?这里就涉及到了信号的扩展,Matlab支持多种扩展模式,可以使用函数dwtmode查询、更改。值得注意的是,只有Periodization模式分解结果长度为N/2,其它模式长度均为floor((N+M-1)/2),为了保证小波分解后总体长度不变,因此这里必须采用Periodization模式;Matlab默认信号扩展模式为Symmetrization(half-point),可以通过dwtmode(‘per’)设置为Periodization模式。
在Matlab中,dwt只能实现单层分解,更强大功能的函数是wavedec函数,可以设置分解层数。前面说了小波分解实际上一个滤波的过程,滤波器的系数的可通过函数wfilters得到,滤波可以通过卷积实现,卷积可以表示为矩阵运算,因此小波分解可以表示为输出向量等于小波变换矩阵乘以输入向量。在这篇博客里,我要得到一个小波变换矩阵,使其等价于Matlab自带的函数dwt和wavedec功能。我的Matlab版本是Version7.9.0.529(R2009b),不知道不同的版本是否会不一样。
在Mallat算法框图中,G1(n)=x(n)*g(n),H1(n)= x(n)*h(n),其中”*”表示卷积。
设x(n)的长度为N,h(n)的长度为M,则H1(n)的长度为N+M-1(假设N>M),以上卷积关系写为矩阵形式:(H1(n)以y(n)表示)
卷积之后还要抽样,每两个点抽一个点,这里dwtmode设置为Periodization模式,因此抽样只有N/2个点,实际上就是对上面由h构成的矩阵的N+M-1行当中抽取N/2行,但抽取哪N/2行呢?通过验证,在MATLAB中是这样子做的,将矩阵的前M/2-1行和后M/2-1行略掉,这样还剩N+M-1-( M/2-1)*2=N+1行,然后抽取其中的偶数行即可得到N/2行,这里假设了M为偶数,而在小波变换中滤波器的长度(h和g的长度)就是偶数。
由于这里dwtmode设置为Periodization模式,即对x进行周期延拓(注:这里x的长度取为2的整数次幂,因此与Periodized Padding模式(可通过dwtmode(‘ppd’)设置)是相同的),因此矩阵每一行实际上应该是h各元素的一个循环移位,因为卷积要反转移位,所以每一行是h各元素倒序的循环移位,当然,由于h的长度小于x,因为要补零的。
有关扩展模式的详细说明参见博文《小波变换中的信号扩展(延拓)问题》。
从由h构成的矩阵抽取N/2行,同理,再从由g构成的矩阵抽取N/2行,上下放在一起可以组成一个N×N的矩阵,即我们要找的小波变换矩阵。
另外,为了实现多层分解,只要用一个矩阵连乘就可以了。从x得到D1和A1的过程(即第一层分解)可以用矩阵表示为:
第二层分解是由A1得到D2和A2的过程,可用矩阵表示如下:
若把第一层分解和第二层分解写在一起,可用分块矩阵的概念表示如下:
第三层分解以此规律类推即可。
理论就阐述这么多,最重要的是给出Matlab程序:
function [ ww ] = dwtmtx( N,wtype,wlev )
%DWTMTX Discrete wavelet transform matrix
% This function generates the transform matrix ww according to input
% parameters N,wtype,wlev .
%Detailed explanation goes here
% N is the dimension of ww
% wtype is the wavelet type
% wlev is the number of decomposition level
%NOTE: The extension mode must be Periodization('per')
[h,g]= wfilters(wtype,'d'); %Decomposition low&high pass filter
L=length(h); %Filter length
h_1 = fliplr(h); %Flip matrix left to right
g_1 = fliplr(g);
loop_max = log2(N);
loop_min = double(int8(log2(L)))+1;
if wlev>loop_max-loop_min+1
fprintf('\nWaring: wlev is too big\n');
fprintf('The biggest wlev is %d\n',loop_max-loop_min+1);
wlev = loop_max-loop_min+1;
end
ww=1;
for loop = loop_max-wlev+1:loop_max
Nii = 2^loop;
p1_0 = [h_1 zeros(1,Nii-L)];
p2_0 = [g_1 zeros(1,Nii-L)];
p1 = zeros(Nii/2,Nii);
p2 = zeros(Nii/2,Nii);
for ii=1:Nii/2
p1(ii,:)=circshift(p1_0',2*(ii-1)+1-(L-1)+L/2-1)';
p2(ii,:)=circshift(p2_0',2*(ii-1)+1-(L-1)+L/2-1)';
end
w1=[p1;p2];
mm=2^loop_max-length(w1);
w=[w1,zeros(length(w1),mm);zeros(mm,length(w1)),eye(mm,mm)];
ww=ww*w;
clear p1;clear p2;
end
%The end!!!
end
为了验证以上的dwtmtx函数是否正确,可以用以下程序验证:
%验证函数dwtmtx的正确性
clear all;close all;clc;
N = 2^7;
% 'db1' or 'haar', 'db2', ... ,'db10', ... , 'db45'
% 'coif1', ... , 'coif5'
% 'sym2', ... , 'sym8', ... ,'sym45'
% 'bior1.1', 'bior1.3', 'bior1.5'
% 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8'
% 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7'
% 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8'
% 'rbio1.1', 'rbio1.3', 'rbio1.5'
% 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8'
% 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7'
% 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8'
wtype = 'rbio6.8';
wlev_max = wmaxlev(N,wtype);
if wlev_max == 0
fprintf('\nThe parameter N and wtype does not match!\n');
end
dwtmode('per');
for wlev = 1:wlev_max
ww = dwtmtx(N,wtype,wlev);
x = randn(1,N);
y1 = (ww*x')';
[y2,y2l] = wavedec(x,wlev,wtype);
y_err = sum((y1-y2).*(y1-y2));
fprintf('wlev = %d: y_err = %f\n',wlev,y_err);
end
其中wtype可以改成上面中的任意一个,即得到不同小波母函数的小波基,通过观察输出结果y_err的值(均为零),说明由dwtmtx函数得到变换矩阵求小波分解系数与Matlab自带的函数wavedec所得结果是一模一样的。
这是不是意味着我得到了小波变换矩阵呢?![]()
【参考文献】
参考文献就写一个网络资源加两本小波分析的Matlab参考书吧,感谢各种网络资源,不能一一列举,从心里表示真诚的感谢!
【1】Compressive sensingfor image using wavelet transform and orthogonal matching pursuit algorithm(measurements in both space domain and wavelet domain areprovided). M-fileDownload (http://www.eee.hku.hk/~wsha/Freecode/Files/Wavelet_OMP.zip)
【2】葛哲学,沙威.小波分析理分与MATLAB R2007实现[M].北京:电子工业出版社,2007.
【3】董长虹. Matlab小波分析工具箱原理与应用[M].北京:国防工业出版社,2004.