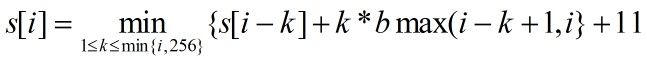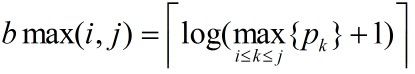0016算法笔记——【动态规划】图像压缩问题

    1、问题描述：

     在计算机中，常用像素点的灰度值序列{p1,p1,……pn}表示图像。其中整数pi,1<=i<=n，表示像素点i的灰度值。通常灰度值的范围是0~255。因此最多需要8位表示一个像素。

      压缩的原理就是把序列{p1,p1,……pn}进行设断点，将其分割成一段一段的。分段的过程就是要找出断点，让一段里面的像素的最大灰度值比较小，那么这一段像素(本来需要8位)就可以用较少的位(比如7位)来表示，从而减少存储空间。

     b代表bits,l代表length,分段是，b[i]表示每段一个像素点需要的最少存储空间(少于8位才有意义)，l[i]表示每段里面有多少个像素点，s[i]表示从0到i压缩为一共占多少存储空间。

     如果限制l[i]<=255,则需要8位来表示l[i]。而b[i]<=8，需要3位表示b[i]。所以每段所需的存储空间为l[i]*b[i]+11位。假设将原图像分成m段，那么需要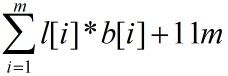位的存储空间。

      图像压缩问题就是要确定像素序列{p1,p1,……pn}的最优分段，使得依此分段所需的存储空间最小。

     2、最优子结构性质

      设l[i],b[i],1<=i<=m是{p1,p1,……pn}的一个最优分段，则l[1],b[1]是{p1,……,pl[1]}的一个最优分段，且l[i],b[i],2<=i<=m是{pl[1]+1,……,pn}的一个最优分段。即图像压缩问题满足最优子结构性质。

     3、递推关系

      设s[i],1<=i<=n是像素序列{p1,p1,……pi}的最优分段所需的存储位数，则s[i]为前i-k个的存储位数加上后k个的存储空间。由最优子结构性质可得：

，式中

         4、构造最优解

     数组l[i],b[i]记录了最优分段所需的信息最优分段的最后一段的段长度和像素位数分别存储在l[n]和b[n]中,其前一段的段长度和像素位数存储于l[n-l[n]]和b[n-l[n]]中，依此类推，可在O(n)时间内构造最优解。

     算法具体实现代码如下：

//3d7 动态规划 图像压缩问题
#include "stdafx.h"
#include <iostream> 
using namespace std; 

const int N = 7;

int length(int i);
void Compress(int n,int p[],int s[],int l[],int b[]);
void Tracebace(int n,int& i,int s[],int l[]);
void Output(int s[],int l[],int b[],int n);

int main()
{
	int p[] = {0,10,12,15,255,1,2};//图像灰度数组 下标从1开始计数
	int s[N],l[N],b[N];

	cout<<"图像的灰度序列为："<<endl;

	for(int i=1;i<N;i++)
	{
		cout<<p[i]<<" ";
	}
	cout<<endl;

	Compress(N-1,p,s,l,b);
	Output(s,l,b,N-1);
	return 0;
}

void Compress(int n,int p[],int s[],int l[],int b[])
{
	int Lmax = 256,header = 11;
	s[0] = 0;
	for(int i=1; i<=n; i++)
	{
		b[i] = length(p[i]);//计算像素点p需要的存储位数
		int bmax = b[i];
		s[i] = s[i-1] + bmax;
		l[i] = 1;

		for(int j=2; j<=i && j<=Lmax;j++)
		{
			if(bmax<b[i-j+1])
			{
				bmax = b[i-j+1];
			}

			if(s[i]>s[i-j]+j*bmax)
			{
				s[i] = s[i-j] + j*bmax;
				l[i] = j;
			}
		}
		s[i] += header;
	}
}

int length(int i)
{
	int k=1;
	i = i/2;
	while(i>0)
	{
		k++;
		i=i/2;
	}
	return k;
}

void Traceback(int n,int& i,int s[],int l[])
{
	if(n==0)
		return;
	Traceback(n-l[n],i,s,l);
	s[i++]=n-l[n];//重新为s[]数组赋值，用来存储分段位置
}

void Output(int s[],int l[],int b[],int n)
{
	//在输出s[n]存储位数后，s[]数组则被重新赋值，用来存储分段的位置
	cout<<"图像压缩后的最小空间为："<<s[n]<<endl;
	int m = 0;
	Traceback(n,m,s,l);
	s[m] = n;
	cout<<"将原灰度序列分成"<<m<<"段序列段"<<endl;
	for(int j=1; j<=m; j++)
	{
		l[j] = l[s[j]];
		b[j] = b[s[j]];
	}
	for(int j=1; j<=m; j++)
	{
		cout<<"段长度："<<l[j]<<",所需存储位数:"<<b[j]<<endl;
	}
}

     算法Compress只需O(n)空间。由于在算法Compress中j的循环次数不超过256,故对每一个确定的i可在O(1)时间内完成。因此整个算法的时间复杂度为O(n)。算法Compress的执行过程可以下图表示：

      方法Output中，在输出s[n]的最小存储空间后，s[]数组被重新赋值，用来存储分段的位置，一边回溯构造最优解。程序运行结果如下：