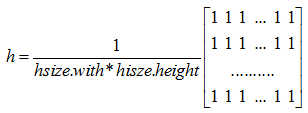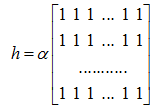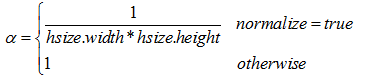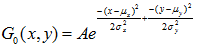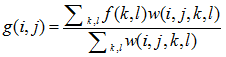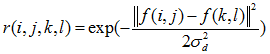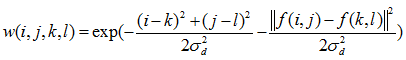【OpenCV】邻域滤波：方框、高斯、中值、双边滤波

转自：http://blog.csdn.net/xiaowei_cqu/article/details/7785365

作者:xiaowei_cqu

 

邻域滤波（卷积）

邻域算子值利用给定像素周围像素的值决定此像素的最终输出。如图左边图像与中间图像卷积禅城右边图像。目标图像中绿色的像素由原图像中蓝色标记的像素计算得到。

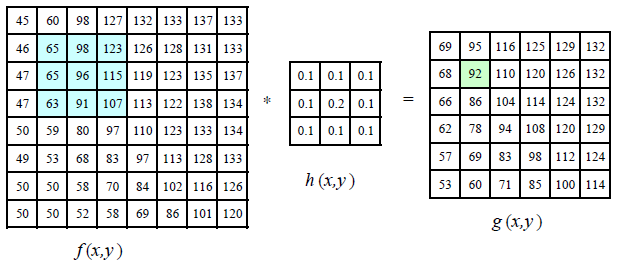
通用线性邻域滤波是一种常用的邻域算子，输入像素加权得到输出像素：

其中权重核   为“滤波系数”。上面的式子可以简记为：

【方框滤波】

最简单的线性滤波是移动平均或方框滤波，用 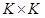窗口中的像素值平均后输出，核函数为：

其实等价于图像与全部元素值为1的核函数进行卷积再进行尺度缩放。

代码

OpenCV中的 blur函数是进行标准方框滤波：

[cpp] view plain copy print ?

void cv::blur( InputArray src, OutputArray dst,
           Size ksize, Point anchor, int borderType )
{
    boxFilter( src, dst, -1, ksize, anchor, true, borderType );
}

而boxFilter函数源码如下：

cv::Ptr<cv::FilterEngine> cv::createBoxFilter( int srcType, int dstType, Size ksize,
                    Point anchor, bool normalize, int borderType )
{
    int sdepth = CV_MAT_DEPTH(srcType);
    int cn = CV_MAT_CN(srcType), sumType = CV_64F;
    if( sdepth <= CV_32S && (!normalize ||
        ksize.width*ksize.height <= (sdepth == CV_8U ? (1<<23) :
            sdepth == CV_16U ? (1 << 15) : (1 << 16))) )
        sumType = CV_32S;
    sumType = CV_MAKETYPE( sumType, cn );

    Ptr<BaseRowFilter> rowFilter = getRowSumFilter(srcType, sumType, ksize.width, anchor.x );
    Ptr<BaseColumnFilter> columnFilter = getColumnSumFilter(sumType,
        dstType, ksize.height, anchor.y, normalize ? 1./(ksize.width*ksize.height) : 1);

    return Ptr<FilterEngine>(new FilterEngine(Ptr<BaseFilter>(0), rowFilter, columnFilter,
           srcType, dstType, sumType, borderType ));
}

这里 blur 和 boxFilter 的区别是，blur是标准化后的 boxFilter，即boxFilter的核函数：

其中，

blur( src, dst, Size( 1, 1 ), Point(-1,-1));
blur( src, dst, Size( 4, 4 ), Point(-1,-1));
blur( src, dst, Size( 8, 8 ), Point(-1,-1));
blur( src, dst, Size( 16, 16 ), Point(-1,-1));   实验结果

下图是对一幅图像分别用1*1,4*4,8*8,16*16标准方框滤波后的图像：

        

【高斯滤波】

高斯滤波器是一类根据高斯函数的形状来选择权值的线性平滑滤波器。它对去除服从正态分布的噪声很有效。
常用的零均值离散高斯滤波器函数：

2D图像中表示为：

代码

/****************************************************************************************\
                                     Gaussian Blur
\****************************************************************************************/

cv::Mat cv::getGaussianKernel( int n, double sigma, int ktype )
{
    const int SMALL_GAUSSIAN_SIZE = 7;
    static const float small_gaussian_tab[][SMALL_GAUSSIAN_SIZE] =
    {
        {1.f},
        {0.25f, 0.5f, 0.25f},
        {0.0625f, 0.25f, 0.375f, 0.25f, 0.0625f},
        {0.03125f, 0.109375f, 0.21875f, 0.28125f, 0.21875f, 0.109375f, 0.03125f}
    };

    const float* fixed_kernel = n % 2 == 1 && n <= SMALL_GAUSSIAN_SIZE && sigma <= 0 ?
        small_gaussian_tab[n>>1] : 0;

    CV_Assert( ktype == CV_32F || ktype == CV_64F );
    Mat kernel(n, 1, ktype);
    float* cf = (float*)kernel.data;
    double* cd = (double*)kernel.data;

    double sigmaX = sigma > 0 ? sigma : ((n-1)*0.5 - 1)*0.3 + 0.8;
    double scale2X = -0.5/(sigmaX*sigmaX);
    double sum = 0;

    int i;
    for( i = 0; i < n; i++ )
    {
        double x = i - (n-1)*0.5;
        double t = fixed_kernel ? (double)fixed_kernel[i] : std::exp(scale2X*x*x);
        if( ktype == CV_32F )
        {
            cf[i] = (float)t;
            sum += cf[i];
        }
        else
        {
            cd[i] = t;
            sum += cd[i];
        }
    }

    sum = 1./sum;
    for( i = 0; i < n; i++ )
    {
        if( ktype == CV_32F )
            cf[i] = (float)(cf[i]*sum);
        else
            cd[i] *= sum;
    }

    return kernel;
}


cv::Ptr<cv::FilterEngine> cv::createGaussianFilter( int type, Size ksize,
                                        double sigma1, double sigma2,
                                        int borderType )
{
    int depth = CV_MAT_DEPTH(type);
    if( sigma2 <= 0 )
        sigma2 = sigma1;

    // automatic detection of kernel size from sigma
    if( ksize.width <= 0 && sigma1 > 0 )
        ksize.width = cvRound(sigma1*(depth == CV_8U ? 3 : 4)*2 + 1)|1;
    if( ksize.height <= 0 && sigma2 > 0 )
        ksize.height = cvRound(sigma2*(depth == CV_8U ? 3 : 4)*2 + 1)|1;

    CV_Assert( ksize.width > 0 && ksize.width % 2 == 1 &&
        ksize.height > 0 && ksize.height % 2 == 1 );

    sigma1 = std::max( sigma1, 0. );
    sigma2 = std::max( sigma2, 0. );

    Mat kx = getGaussianKernel( ksize.width, sigma1, std::max(depth, CV_32F) );
    Mat ky;
    if( ksize.height == ksize.width && std::abs(sigma1 - sigma2) < DBL_EPSILON )
        ky = kx;
    else
        ky = getGaussianKernel( ksize.height, sigma2, std::max(depth, CV_32F) );

    return createSeparableLinearFilter( type, type, kx, ky, Point(-1,-1), 0, borderType );
}


void cv::GaussianBlur( InputArray _src, OutputArray _dst, Size ksize,
                   double sigma1, double sigma2,
                   int borderType )
{
    Mat src = _src.getMat();
    _dst.create( src.size(), src.type() );
    Mat dst = _dst.getMat();

    if( borderType != BORDER_CONSTANT )
    {
        if( src.rows == 1 )
            ksize.height = 1;
        if( src.cols == 1 )
            ksize.width = 1;
    }

    if( ksize.width == 1 && ksize.height == 1 )
    {
        src.copyTo(dst);
        return;
    }

#ifdef HAVE_TEGRA_OPTIMIZATION
    if(sigma1 == 0 && sigma2 == 0 && tegra::gaussian(src, dst, ksize, borderType))
        return;
#endif

    Ptr<FilterEngine> f = createGaussianFilter( src.type(), ksize, sigma1, sigma2, borderType );
    f->apply( src, dst );
}

 

实验结果

下图是对一幅图像分别用1*1,3*3,5*5,9*9标准方框滤波后的图像：

        

 

非线性滤波

线性滤波易于构造，且易于从频率响应的角度分析，但如果噪声是散粒噪声而非高斯噪声时线性滤波不能去除噪声。如图像突然出现很大的值，线性滤波只是转换为柔和但仍可见的散粒。这时需要非线性滤波。

简单的非线性滤波有 中值滤波， -截尾均值滤波，定义域滤波 和值域滤波 。

中值滤波选择每个邻域像素的中值输出； -截尾均值滤波是指去掉百分率为 的最小值和最大值；定义域滤波中沿着边界的数字是像素的距离；值域就是去掉值域外的像素值。

中值滤波代码

medianBlur ( src, dst, i );

中值滤波实验

下图是对一幅图像分别用3*3,5*5,7*7,9*9（这里必须是奇数）标准方框滤波后的图像：

        

 

【双边滤波】

双边滤波的思想是抑制与中心像素值差别太大的像素，输出像素值依赖于邻域像素值的加权合：

权重系数 取决于定义域核

 

和依赖于数据的值域核

 

的乘积。相乘后会产生依赖于数据的双边权重函数：

双边滤波源码

/****************************************************************************************\
                                   Bilateral Filtering
\****************************************************************************************/

namespace cv
{

static void
bilateralFilter_8u( const Mat& src, Mat& dst, int d,
                    double sigma_color, double sigma_space,
                    int borderType )
{
    int cn = src.channels();
    int i, j, k, maxk, radius;
    Size size = src.size();

    CV_Assert( (src.type() == CV_8UC1 || src.type() == CV_8UC3) &&
        src.type() == dst.type() && src.size() == dst.size() &&
        src.data != dst.data );

    if( sigma_color <= 0 )
        sigma_color = 1;
    if( sigma_space <= 0 )
        sigma_space = 1;

    double gauss_color_coeff = -0.5/(sigma_color*sigma_color);
    double gauss_space_coeff = -0.5/(sigma_space*sigma_space);

    if( d <= 0 )
        radius = cvRound(sigma_space*1.5);
    else
        radius = d/2;
    radius = MAX(radius, 1);
    d = radius*2 + 1;

    Mat temp;
    copyMakeBorder( src, temp, radius, radius, radius, radius, borderType );

    vector<float> _color_weight(cn*256);
    vector<float> _space_weight(d*d);
    vector<int> _space_ofs(d*d);
    float* color_weight = &_color_weight[0];
    float* space_weight = &_space_weight[0];
    int* space_ofs = &_space_ofs[0];

    // initialize color-related bilateral filter coefficients
    for( i = 0; i < 256*cn; i++ )
        color_weight[i] = (float)std::exp(i*i*gauss_color_coeff);

    // initialize space-related bilateral filter coefficients
    for( i = -radius, maxk = 0; i <= radius; i++ )
        for( j = -radius; j <= radius; j++ )
        {
            double r = std::sqrt((double)i*i + (double)j*j);
            if( r > radius )
                continue;
            space_weight[maxk] = (float)std::exp(r*r*gauss_space_coeff);
            space_ofs[maxk++] = (int)(i*temp.step + j*cn);
        }

    for( i = 0; i < size.height; i++ )
    {
        const uchar* sptr = temp.data + (i+radius)*temp.step + radius*cn;
        uchar* dptr = dst.data + i*dst.step;

        if( cn == 1 )
        {
            for( j = 0; j < size.width; j++ )
            {
                float sum = 0, wsum = 0;
                int val0 = sptr[j];
                for( k = 0; k < maxk; k++ )
                {
                    int val = sptr[j + space_ofs[k]];
                    float w = space_weight[k]*color_weight[std::abs(val - val0)];
                    sum += val*w;
                    wsum += w;
                }
                // overflow is not possible here => there is no need to use CV_CAST_8U
                dptr[j] = (uchar)cvRound(sum/wsum);
            }
        }
        else
        {
            assert( cn == 3 );
            for( j = 0; j < size.width*3; j += 3 )
            {
                float sum_b = 0, sum_g = 0, sum_r = 0, wsum = 0;
                int b0 = sptr[j], g0 = sptr[j+1], r0 = sptr[j+2];
                for( k = 0; k < maxk; k++ )
                {
                    const uchar* sptr_k = sptr + j + space_ofs[k];
                    int b = sptr_k[0], g = sptr_k[1], r = sptr_k[2];
                    float w = space_weight[k]*color_weight[std::abs(b - b0) +
                        std::abs(g - g0) + std::abs(r - r0)];
                    sum_b += b*w; sum_g += g*w; sum_r += r*w;
                    wsum += w;
                }
                wsum = 1.f/wsum;
                b0 = cvRound(sum_b*wsum);
                g0 = cvRound(sum_g*wsum);
                r0 = cvRound(sum_r*wsum);
                dptr[j] = (uchar)b0; dptr[j+1] = (uchar)g0; dptr[j+2] = (uchar)r0;
            }
        }
    }
}

双边滤波调用

bilateralFilter(InputArray src, OutputArray dst, int d, double sigmaColor, double sigmaSpace,
                      int borderType=BORDER_DEFAULT )；

d 表示滤波时像素邻域直径，d为负时由 sigaColor计算得到；d>5时不能实时处理。

sigmaColor、sigmaSpace非别表示颜色空间和坐标空间的滤波系数sigma。可以简单的赋值为相同的值。<10时几乎没有效果；>150时为油画的效果。

borderType可以不指定。

双边滤波实验

用sigma为10，150,240,480时效果如下：

          

参考文献：

Richard Szeliski 《Computer Vision: Algorithms and Applications》
http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html
《The OpenCV Tutorials》 Release 2.4.2
《The OpenCV Reference Manual 》 Release 2.4.2