Ng机器学习系列补充：2、分类和回归树算法CART
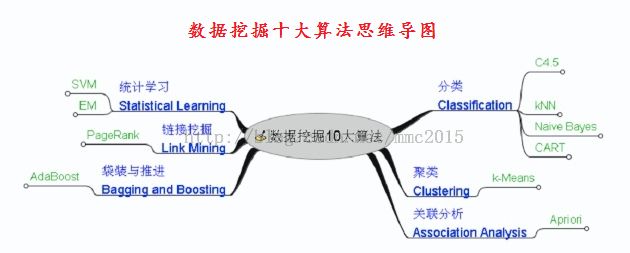
机器学习补充系列国际权威的学术组织the IEEE International Conference on Data Mining (ICDM，国际数据哇局会议) 2006年12月评选出了数据挖掘领域的十大经典算法：C4.5, k-Means, SVM, Apriori, EM, PageRank, AdaBoost, kNN, Naive Bayes, and CART，它们在数据挖掘领域都产生了极为深远的影响，这里对他们做一个简单介绍，仅作为对Ng机器学习教程的补充。
由于k-Means、SVM、EM、kNN、Naive Bayes在Ng的系列教程中都有涉及，所以此系列教程只涉及决策树算法C4.5、关联规则算法Apriori、网页排名算法PageRank、集成学习算法AdaBoost(Adaptive Boosting，自适应推进)、分类与回归树算法CART(Classification and Regression Trees)；另外会加上对神经网络的BP算法介绍，后续也会考虑介绍遗传算法等内容。
1）算法思想
2）递归划分举例说明
3）CART算法、C5.0算法和CHAID算法比较
1）算法思想
分类和回归树算法CART（Classification And Regression Tree）采用一种二分递归分割的技术，将当前的样本集分为两个子样本集，使得生成的的每个非叶子节点都有两个分支。因此，CART算法生成的决策树是结构简洁的二叉树。
分类树两个基本思想：利用训练样本，递归地划分自变量空间进行建树的思想；用验证数据进行剪枝。
递归划分：用变量y表示因变量（分类变量），用x1, x2, x3,...,xp表示自变量。通过递归的方式把关于自变量x的p维空间划分为不重叠的超矩形。首先，一个自变量被选择，比如xi和xi的一个值si被选择，它把p维空间分成两部分：一部分是p维的超矩形，其中包含的点都满足xi<=si，另一个p维超矩形包含所有的点满足xi>si（这个过程其实描述的回归的情况）。接着，这两部分中的每一个部分通过选择一个变量和该变量的划分值以相似的方式被划分（从这里往后我们把超矩形都说成矩形）。随着这个过程的持续，我们得到的矩形越来越小，直到每个小矩形都尽可能是同构的或“纯”的，“纯”的意思是（矩形）所包含的点都属于同一类或者只有一个样本（当然，这不总是可能的，因为经常存在一些属于不同类的点，但这些点的自变量有完全相同的值，我们认为包含的点都只属于一个类）。
具体的划分方式：（这个过程其实描述的分类的情况）分它检查每个变量和该变量所有可能的划分值来发现最好的划，对离散值如{x,y,x}，则在该属性上的划分有三种情况({{x,y},{z}},{{x,z},y},{{y,z},x})，空集和全集的划分除外；对于连续值处理引进“分裂点”的思想，假设样本集中某个属性共n个连续值，则有n-1个分裂点，每个“分裂点”为相邻两个连续值的均值 (a[i] + a[i+1]) / 2。将每个属性的所有划分按照他们能减少的杂质量来进行排序，目前最流行的杂质度量方法是：GINI指标（对于连续的目标变量，可以使用最小二乘偏差（LSD）或最小绝对偏差（LAD），这里只考虑GINI指标）。如果分类变量y的取值为1,2,3……C，一个节点A的GINI不纯度定义为：
，其中，Pk表示观测点中属于k类得概率，当Gini(A)=0时所有样本属于同一类，当所有类在节点中以相同的概率出现时，Gini(A)最大化，此时值为(C-1)C/2。
验证剪枝：在决策树构造时，由于训练数据中的噪音或孤立点，许多分枝反映的是训练数据中的异常，使用这样的判定树对类别未知的数据进行分类，分类的准确性不高。决策树常用的剪枝方法有事前剪枝和事后剪枝，CART算法经常采用事后剪枝方法：等树已经完全生成后，再检查并删除异常节点的分支。
CART用的成本复杂性标准是Err(T)+a|L(T)|，其中Err(T)是验证数据被树T误分部分，a|L(T)|是对树的大小的惩罚因素，L(T)是树T的叶节点数，a是每个节点的惩罚成本：一个从0向上变动的数字。当a=0时表示不管树的节点的多少，都不进行惩罚。在剪枝形成的一系列树中，从其中选择一个在验证数据集上具有最小误分的树是很自然的，我们把这个树成为最小误分树。
2）递归划分举例说明
还是决策树中的例子：
我们先根据Outlook条件属性计算GINI，Outlook有三个属性值，因为CART是一个二叉树，我们把三个属性值按照2+1的组合（有三种）即：
针对第一个表：
，
我们得出第一个GINI的增益（GINI_Gain，这里用GINI表示）：
针对第二个表：
，
我们得出第二个GINI的增益（GINI_Gain，这里用GINI表示）：
针对第三个表：
，
我们得到第三个GINI的增益（GINI_Gain，这里用GINI表示）：
3）CART算法、C5.0算法和CHAID算法比较
| C5.0 | CART |
CHAID | |
| 输出变量 | 只能是分类型 | 可以是分类型也可以是数值型 | 可以是分类型 也可以是数值型 |
| 建树类型 | 只能建分类树 | 既可建分类树又可建回归树 | 能够建立多叉树 |
| 树 | 可建多叉树 | 只能建二叉树 | 能够建立多叉树 |
| 确定最佳分类变量和分割点依据 | 以信息熵为基础 通过计算信息增益确定 |
以Gini系数和方差作为选择依据 | 从统计显著性检验角度确定 |
| 决定决策树的标准 | 依据训练样本 通过近似正态分布确定 |
依据测试样本进行修剪 | 从统计显著性检验角度确定 |
http://blog.csdn.net/aladdina/article/details/4141150
http://blog.csdn.net/hewei0241/article/details/8280490
http://blog.163.com/li_205213/blog/static/1178967932014520112938956/
http://www.dataguru.cn/article-4720-1.html