最短路径(四)—Bellman-Ford的队列优化(邻接表)
上一节我们写了Bellman-Ford算法解决负权边的问题:
http://blog.csdn.net/wtyvhreal/article/details/43450727
当谈到对Bellman-Ford算法的优化时,我们提出了两种优化方案,其中第一种已经给出了解决方案,那么第二种优化方案:
优化二:
在每次松弛后,会有一些顶点已经求得了最短路,此后这些顶点的最短路估计值就会一直保持不变,不再受后续松弛的影响,但是每次还要判断是否需要松弛,这里浪费了时间,所以
需要:每次仅对最短路径估计值发生变化了的顶点的所有出边执行松弛操作。
邻接表存储图:
n个顶点,m条边。
数组实现邻接表。对每一条边进行1-m编号。用u,v,w三个数组来记录每条边的信息,即u[i],v[i],w[i]表示第i条边是从第 u[i]号顶点到v[i]号顶点且权值为w[i].
first数组的1-n号单元格分别用来存储1-n号顶点的第一条边的编号,初始的时候因为没有边加入所有都是-1.即first[u[i]]保存顶点u[i]的第一条边的编号,next[i]存储“编号为i的边”的“下一条边”的编号。
接下来遍历边。遍历1号订单的每一条边。
在找到1号顶点的第一条边之后,剩下得边都可以在next数组中一次找到
此时遍历某个顶点的边的时候的遍历顺序正好与读入时候的顺序相反。因为在为每个顶点插入边的时候都是直接插入“链表”的首部而不是尾部。
用临接表来存储图的时间空间复杂度是O(M),遍历每一条边的时间复杂度也是O(M),如果一个图是稀疏图的话,M要远小于N^2,因此稀疏图选用邻接表来存储比用邻接矩阵来存储好很多。
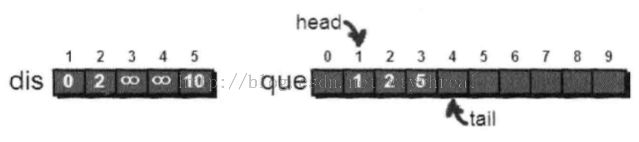
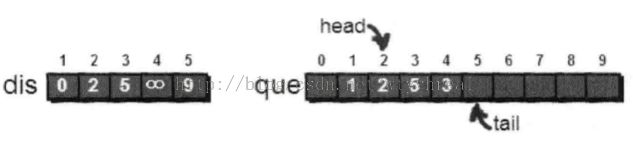
Bellman-Ford的队列优化
上一篇中我们提到的Bellman-Ford算法的第二种优化:每次仅对最短路径发生变化了的点的相邻边执行松弛操作。
每次选取队首顶点u,对顶点u的所有出边进行松弛操作。例如有一条u->v的边,如果通过u->v这条边使得源点到顶点v的最短路径变短,且顶点v不在当前的队列中,将顶点v放入队尾。(但是一个点可以出去以后,再次入队列)。在对顶点u的所有出边松弛完毕后,将顶点u出队。接下来不断从队列中取出新的队首顶点在进行如上操作,直至队列空为止。
代码实现,用邻接表存储这个图:
运行结果:
![]()
使用队列优化的Bellman-Ford算法的时间复杂度在最坏的情况下也是O(NM).通过队列优化的Bellman-Ford中,如果某个点进入队列的次数超过n次,那么这个图则肯定存在负环。