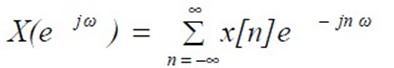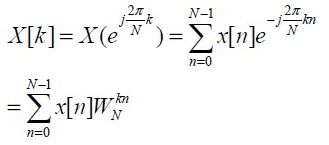各种傅里叶变换的区别

http://blog.csdn.net/xuexiang0704/article/details/8295425
1.DFT DTFT FFT有啥区别
对于一般的周期信号可以用一系列(有限个或者无穷多了)正弦波的叠加来表示。这些正弦波的频率都是某一个特定频率的倍数如5hz、2*5hz、3*5hz……(其中的5hz叫基频)。这是傅立叶级数的思想,所以说周期信号的频率是离散的。 而且,周期信号有一个特点,![]() 【信号的周期越长,信号的基频越小。】
【信号的周期越长,信号的基频越小。】![]() 【 非周期信号可以看作周期无穷大的周期信号,那么它的基频就是无穷小,这样它的频率组成就变成了连续的了。】求这个连续频率的谱线的过程就是傅立叶变换。包括这样几种:
【 非周期信号可以看作周期无穷大的周期信号,那么它的基频就是无穷小,这样它的频率组成就变成了连续的了。】求这个连续频率的谱线的过程就是傅立叶变换。包括这样几种:
DTFT(时间离散,频率连续),即 针对的是连续的信号和频谱。
DFT(时间和频率都离散,可在计算机中处理),针对的是离散的信号和频谱。
FFT(DFT的优化算法,计算量减少)
![]() 【DTFT是对任意序列的傅里叶分析,它的频谱是一个连续函数;而DFT是把有限长序列作为周期序列的一个周期,对有限长序列的傅里叶分析,DFT的特点是无论在时域还是频域都是有限长序列。 】
【DTFT是对任意序列的傅里叶分析,它的频谱是一个连续函数;而DFT是把有限长序列作为周期序列的一个周期,对有限长序列的傅里叶分析,DFT的特点是无论在时域还是频域都是有限长序列。 】![]()
2.离散傅里叶变换DFT和离散时间傅里叶变换DTFT的区别是啥
离散时间傅里叶变换有时也称为序列傅里叶变换。离散时间傅里叶变换实质上就是单位圆上的(双边)Z变换。当时域信号为连续信号时,用连续时间傅里叶变换;为离散信号时,用离散时间傅里叶变换。
离散时间傅里叶变换(DTFT,Discrete Time Fourier Transform)使我们能够在频域(数字频域)分析离散时间信号的频谱和离散系统的频响特性。但还存在两个实际问题。
1. 数字频率是一个模拟量,为了便于今后用数字的方法进行分析和处理,仅仅在时域将时间变量t离散化还不够,还必须在频域将数字频率离散化。
2. 实际的序列大多为无限长的,为了分析和处理的方便,必须把无限长序列截断或分段,化作有限长序列来处理。
【另一篇相关的】
1.1
时域上任意连续的周期信号可以分解为无限多个正弦信号之和,在频域上就表示为离散非周期的信号,即时域连续周期对应频域离散非周期的特点,这就是傅立叶级数展开(FS),它用于分析连续周期信号。
FT是傅立叶变换,它主要用于分析连续非周期信号,由于信号是非周期的,它必包含了各种频率的信号,所以具有时域连续非周期对应频域连续非周期的特点。
FS和FT 都是用于连续信号频谱的分析工具,它们都以傅立叶级数理论问基础推导出的。时域上连续的信号在频域上都有非周期的特点,但对于周期信号和非周期信号又有在频域离散和连续之分。
在自然界中除了存在温度,压力等在时间上连续的信号,还存在一些离散信号,离散信号可经过连续信号采样获得,也有本身就是离散的。例如,某地区的年降水量或平均增长率等信号,这类信号的时间变量为年,不在整数时间点的信号是没有意义的。用于离散信号频谱分析的工具包括DFS,DTFT和DFT。
1.2
DTFT是离散时间傅立叶变换,它用于离散非周期序列分析,根据连续傅立叶变换要求连续信号在时间上必须可积这一充分必要条件,那么对于离散时间傅立叶变换,用于它之上的离散序列也必须满足在时间轴上级数求和收敛的条件;由于信号是非周期序列,它必包含了各种频率的信号,所以DTFT对离散非周期信号变换后的频谱为连续的,即有时域离散非周期对应频域连续周期的特点。
当离散的信号为周期序列时,严格的讲,傅立叶变换是不存在的,因为它不满足信号序列绝对级数和收敛(绝对可和)这一傅立叶变换的充要条件,但是采用DFS(离散傅立叶级数)这一分析工具仍然可以对其进行傅立叶分析。
那么面对离散周期信号我们还有其它的分析方法了么????
我们知道周期离散信号是由无穷多相同的周期序列在时间轴上组成的,假设周期为N,即每个周期序列都有N个元素,而这样的周期序列有无穷多个,由于无穷多个周期序列都相同,所以可以只取其中一个周期就足以表示整个序列了,这个被抽出来表示整个序列特性的周期称为主值周期,这个序列称为主值序列。然后以N对应的频率作为基频构成傅立叶级数展开所需要的复指数序列ek(n)=exp(j*2pi*k*n/N),用主值序列与复指数序列取相关(乘加运算),得出每个主值在各频率上的频谱分量,这样就表示出了周期序列的频谱特性。
根据DTFT,对于有限长序列作Z变换或序列傅立叶变换都是可行的,或者说,有限长序列的频域和复频域分析在理论上都已经解决;但对于数字系统,无论是Z变换还是序列傅立叶变换的适用方面都存在一些问题,重要是因为频率变量的连续性性质(DTFT变换出连续频谱),不便于数字运算和储存。
参考DFS,可以采用类似DFS的分析方法对解决以上问题。![]() 可以把有限长非周期序列假设为一无限长周期序列的一个主值周期
可以把有限长非周期序列假设为一无限长周期序列的一个主值周期![]() ,即对有限长非周期序列进行周期延拓,延拓后的序列完全可以采用DFS进行处理,即采用复指数基频序列和此有限长时间序列取相关,得出每个主值在各频率上的频谱分量以表示出这个"主值周期"的频谱信息。
,即对有限长非周期序列进行周期延拓,延拓后的序列完全可以采用DFS进行处理,即采用复指数基频序列和此有限长时间序列取相关,得出每个主值在各频率上的频谱分量以表示出这个"主值周期"的频谱信息。
由于DFT借用了DFS,这样就假设了序列的周期无限性,但在处理时又对区间作出限定(主值区间),以符合有限长的特点,这就使DFT带有了周期性。另外,DFT只是对一周期内的有限个离散频率的表示,所以它在频率上是离散的,就相当于DTFT变换成连续频谱后再对其采样,此时采样频率等于序列延拓后的周期N,即主值序列的个数。
序列x[n] 的DTFT 定义:
N 点序列x[n] 的DFT 定义:
DFT和DTFT都是频域上的分析,至于Z变换,是在时域上的分析,我们习惯叫Z域。Z变换主要的作用是通过分析信号或者脉冲响应的零点和极点,来得知其稳定性和时域上的特性。
对信号处理来首,时域和频域上的分析和处理都是必须的。
DFS和DFT的关系;DTFT和DFT的关系
计算机能够处理的信号时离散的数字信号,因此必须对模拟信号进行采样,采样信号满足fs>2*f0。同时,输出的频率也必须是离散的,这样计算机才能处理或保存。
我们知道离散的采样信号在频域具有周期性,因此DTFT(离散时间傅里叶变换,对模拟信号进行采样后获得,采样频率满足fs>2*f0)具有周期性,我们只对其主周期[-π,π)或者[0,2π)进行分析,对于整个频谱[-∞,+∞]我们可以进行周期性的拓展获得