POJ2513解题报告
POJ2513题目链接
以为是很简单的字典树……哭……
欧拉回路以前貌似用过,还有一点印象,并查集是真的没有用过,各种搜索,附一些链接,并写写自己的总结~
欧拉回路:
1 定义
欧拉通路 (欧拉迹) ——通过图中每条边一次且仅一次,并且过每一顶点的通路。
欧拉回路 (欧拉闭迹) ——通过图中每条边一次且仅一次,并且过每一顶点的回路。
欧拉图 ——存在欧拉回路的图。
2 无向图是否具有欧拉通路或回路的判定
G有欧拉通路的充分必要条件为:G 连通,G中只有两个奇度顶点(它们分别是欧拉通路的两个端点)。
G有欧拉回路(G为欧拉图):G连通,G中均为偶度顶点。
3 有向图是否具有欧拉通路或回路的判定
D有欧拉通路:D连通,除两个顶点外,其余顶点的入度均等于出度,这两个特殊的顶点中,一个顶点的入度比出度大1,另一个顶点的入度比出度小1。
D有欧拉回路(D为欧拉图):D连通,D中所有顶点的入度等于出度。
在这个问题里面,需要进行判定的就是没有超过两个以上的奇数个点,并且是联通的。是否为奇数可以用一个暂存的数组保存之,是否连通需要并查集的知识了,下面先贴链接,再说自己的想法:(写到这里真是后悔之前做POJ没有写过解题报告,那一百多道题真是做了就忘了……浪费啊……可耻啊……教训啊……)
这个哥们的并查集总结比较详细,对原理什么的说的也比较清楚:链接
这个是大牛,里面的东西很多,贴之Mark之羡慕嫉妒恨之
=============================从这里开始摘自第一个链接====================================
l 并查集:(union-find sets)
一种简单的用途广泛的集合. 并查集是若干个不相交集合,能够实现较快的合并和判断元素所在集合的操作,应用很多,如其求无向图的连通分量个数等。最完美的应用当属:实现Kruskar算法求最小生成树。
l 并查集的精髓(即它的三种操作,结合实现代码模板进行理解):
1、Make_Set(x) 把每一个元素初始化为一个集合
初始化后每一个元素的父亲节点是它本身,每一个元素的祖先节点也是它本身(也可以根据情况而变)。
2、Find_Set(x) 查找一个元素所在的集合
查找一个元素所在的集合,其精髓是找到这个元素所在集合的祖先!这个才是并查集判断和合并的最终依据。
判断两个元素是否属于同一集合,只要看他们所在集合的祖先是否相同即可。
合并两个集合,也是使一个集合的祖先成为另一个集合的祖先,具体见示意图
3、Union(x,y) 合并x,y所在的两个集合
合并两个不相交集合操作很简单:
利用Find_Set找到其中两个集合的祖先,将一个集合的祖先指向另一个集合的祖先。如图
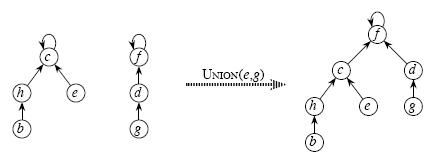
l 并查集的优化
1、Find_Set(x)时 路径压缩
寻找祖先时我们一般采用递归查找,但是当元素很多亦或是整棵树变为一条链时,每次Find_Set(x)都是O(n)的复杂度,有没有办法减小这个复杂度呢?
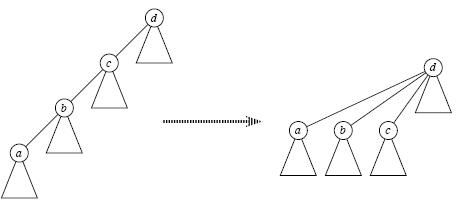
答案是肯定的,这就是路径压缩,即当我们经过"递推"找到祖先节点后,"回溯"的时候顺便将它的子孙节点都直接指向祖先,这样以后再次Find_Set(x)时复杂度就变成O(1)了,如下图所示;可见,路径压缩方便了以后的查找。
2、Union(x,y)时 按秩合并
即合并的时候将元素少的集合合并到元素多的集合中,这样合并之后树的高度会相对较小。
1int father[MAX]; /**//* father[x]表示x的父节点*/ 2int rank[MAX]; /**//* rank[x]表示x的秩*/ 3 4 5/**//* 初始化集合*/ 6void Make_Set(int x) 7{ 8 father[x] = x; //根据实际情况指定的父节点可变化 9 rank[x] = 0; //根据实际情况初始化秩也有所变化 10} 11 12 13/**//* 查找x元素所在的集合,回溯时压缩路径*/ 14int Find_Set(int x) 15{ 16 if (x != father[x]) 17 { 18 father[x] = Find_Set(father[x]); //这个回溯时的压缩路径是精华 19 } 20 return father[x]; 21} 22 23 24/**//* 25 按秩合并x,y所在的集合 26 下面的那个if else结构不是绝对的,具体根据情况变化 27 但是,宗旨是不变的即,按秩合并,实时更新秩。 28*/ 29void Union(int x, int y) 30{ 31 x = Find_Set(x); 32 y = Find_Set(y); 33 if (x == y) return; 34 if (rank[x] > rank[y]) 35 { 36 father[y] = x; 37 } 38 else 39 { 40 if (rank[x] == rank[y]) 41 { 42 rank[y]++; 43 } 44 father[x] = y; 45 } 46}
=================================摘抄完毕===============================
简单的来说,并查集也是一种做记录的方式对集合进行合并:
1. 使能连接到同一元素的元素们指向相同的根,以此来代表他们属于同一个集合。
2. 合并的时候根据rank的大小来合并,把小树合并到大树中去,这样能够有效的减小树的高度。
3. 文中强调的一点,"回溯"的时候顺便将它的子孙节点都直接指向祖先。
最后字典树就没有什么好说的了,AC的代码:
#include <stdio.h> #include <string.h> const int MAXSIZE = 500002; char s1[11],s2[11]; short p[MAXSIZE]; short r[MAXSIZE]; short degree[250001]; int num; struct TreeNode { int id;//the id of the string struct TreeNode * next[26]; TreeNode ():id(0) { memset(next,NULL,26*sizeof(TreeNode*)); } }; TreeNode * root; int Insert(char *s) { TreeNode *p = root; int i = 0; int l = strlen(s); for(i=0;i<l;i++) { if(p->next[s[i]-'a']==NULL) p->next[s[i]-'a']=new TreeNode; p=p->next[s[i]-'a']; } if(p->id==0)//first insert p->id = ++num; return p->id; } void MakeSet(int x) { p[x]=x; r[x]=1; } int FindSet(int x) {//这里不把递归修正为while循环的目的是随着递归修正父节点!!! if(p[x]!=x) p[x]=FindSet(p[x]); return p[x]; } void UnionSet(int x,int y) { if(x == y) return; if(r[x]>r[y]) p[y]=x; else { if(r[x] == r[y]) ++r[y]; p[x]=y; } } int main() { root = new TreeNode; for (int i = 0;i<MAXSIZE;++i) p[i] = i; int id1,id2,sum=0; while(scanf("%s %s",s1,s2)!=EOF) { id1 = Insert(s1); id2 = Insert(s2); ++degree[id1]; ++degree[id2]; UnionSet(FindSet(id1),FindSet(id2)); } for(int i=1;i<num;++i) { if(degree[i] & 0x00000001) ++sum; if(sum>2) { printf("Impossible/n"); return 0; } } for(int i=1;i<num;++i) if(FindSet(i) != FindSet(1)) { printf("Impossible/n"); return 0 ; } printf("Possible/n"); return 0; }
以此为基础,顺便A掉了2524和1611(都是并查集的题目,比较简单)。
现在在尝试写FindSet的非递归版本,代码如下~
非递归版本的FindSet函数实现:
int FindSet(int x) { int y,z,root; y = p[x]; p[x] = x; while (x != y) {//first loop is to find the root z= p[y]; p[y] = x;//reversing parent's pointer! y = z;// point to their father, respectively x = y; } root = x;//x==y now y = p[x];//the pointer has been reversed! p[x] = root; while (x != y) {//the second loop is re-new the pointer z= p[y]; p[y] = root;//reversing parent's pointer! x = y; y = z;// point to their father, respectively } return root; }
这个函数的实现其实在本质上就是要理解路径压缩的过程,原来的递归版本其实是一种两趟搜索的方法,一趟沿查找路径上升,直到找到根;一趟沿查找路径下降,以便更新每一个节点,使之直接指向根(摘自算法导论SE P.311)。
非递归的办法也是使用while循环模拟这种两趟的过程,第一个循环让根指向元素,第二个循环则把对应元素的根全部用最终的root来代替,最后返还root。
POJ1161-Code
//最小并查集 #include <stdio.h> #include <memory.h> int p[30010]; int r[30010]; void Initialize(int n) { for (int i = 0;i<=n;++i) { p[i] = i; r[i] = 1; } //memset(r,0,sizeof(r)); } int FindSet(int x) { // if(x!=p[x]) // p[x] = FindSet(p[x]); // return p[x]; int y,z,root; y = p[x]; p[x] = x; while (x != y) {//first loop is to find the root z= p[y]; p[y] = x;//reversing parent's pointer! y = z;// point to their father, respectively x = y; } root = x;//x==y now y = p[x];//the pointer has been reversed! p[x] = root; while (x != y) {//the second loop is re-new the pointer z= p[y]; p[y] = root;//reversing parent's pointer! x = y; y = z;// point to their father, respectively } return root; } void UnionSet(int x, int y) { // if(x == y) // return; // if(r[x]<=r[y]) // { // p[x] = y; // r[y]+=r[x]; // } // else // { // p[y] = x; // r[x]+=r[y]; // } if(x == y) return; if(r[x]<r[y]) { p[x] = y; } else { p[y] = x; } if(r[x] == r[y]) ++r[y]; } int main() { int n ,m; while (scanf("%d%d",&n,&m),m|n) { Initialize(n); int cnt = 0; for (int i = 0;i<m;++i) { int k,id1,id2; scanf("%d%d",&k,&id1); while (--k) { scanf("%d",&id2); UnionSet(FindSet(id1),FindSet(id2)); } } for (int i = 0;i<n;++i) { if(FindSet(0)==FindSet(i)) ++cnt; } printf("%d/n",cnt); //printf("%d[%d]/n",FindSet(0),r[FindSet(0)]); } return 0; }
POJ2524-Code
#include <stdio.h> const int MAXSIZE = 50001; int p[MAXSIZE]; int rank[MAXSIZE]; void Initialize(int n) { for (int i = 1;i<=n;++i) { p[i] = i; rank[i] = 1; } p[0] = n; //memset(r,0,sizeof(r)); } int FindSet(int x) { if(x!=p[x]) p[x] = FindSet(p[x]); return p[x]; } void UnionSet(int x, int y) { if(x == y) return; if(rank[x]<rank[y]) { p[x] = y; } else { p[y] = x; } if(rank[x] == rank[y]) ++rank[y]; --p[0]; } int main() { int n,m,num= 0; while (scanf("%d%d",&n,&m),m|n) { ++num; int x,y; Initialize(n); while (m--) { scanf("%d%d",&x,&y); UnionSet(FindSet(x),FindSet(y)); } printf("Case %d: %d/n",num,p[0]); } return 0; }
对于2524一个简单说说的地方就是把P[0]作为记录子树数目的节点,初始化为n,当执行Union操作的时候,如果x!=y则执行--p[0]。