ZOJ Monthly, December 2013
部分题解(3738,3740,3741,3742,3745),其他题目以后会做了再更新吧。。。
ZOJ 3738 Buy the Pets
状压dp,如果压20位(10位猫,10位狗),显然复杂度不够。
观察一下发现人和猫有冲突,狗和猫有冲突,人和狗无冲突。那么可以压10位,人选猫,狗选猫,再乘起来就是答案。复杂度O(10*10*2^10)。
转移:
dp[i][1<<j^st]+=dp[i-1][st] (i与j不冲突)
dp[i][st]+=dp[i-1][st]
code:
#include <algorithm>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
#define N 50100
#define ll long long
#define ALL(x) x.begin(),x.end()
#define CLR(x,a) memset(x,a,sizeof(x))
typedef pair<int,int> PI;
const int INF=0x3fffffff;
const int MOD=1000000007;
const double EPS=1e-9;
/*----------------code-----------------*/
bool r[2][16][16];
ll dp[2][16][1<<10];
int p,c,d,m;
int who(int &x){
int type=0;
x--;
if(x-p>=0) x-=p, type++; else return type;
if(x-c>=0) x-=c, type++;
return type;
}
void DP(int n,bool (*g)[16],ll (*f)[1<<10]){
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<(1<<c);j++){
f[i][j]+=f[i-1][j];
for(int k=0;k<c;k++) if(!(1<<k&j)){
if(g[i-1][k]) continue;
f[i][1<<k^j]+=f[i-1][j];
}
}
}
}
int main(){
while(~scanf("%d%d%d",&p,&c,&d)){
scanf("%d",&m);
CLR(r,0);
CLR(dp,0);
while(m--){
int x,y;
scanf("%d%d",&x,&y);
int u=who(x),v=who(y),op=(u+v)%3;
if(v!=1) swap(x,y);
r[op][x][y]=true;
}
DP(p,r[1],dp[1]); //people choose cat
DP(d,r[0],dp[0]); //dog choose cat
ll ans=0;
for(int i=0;i<(1<<c);i++){
if(__builtin_popcount(i)!=p) continue;
ans+=dp[1][p][i]*dp[0][d][i];
}
printf("%lld\n",ans);
}
return 0;
}
ZOJ 3740 Water Level
对于每个A[i],有一个区间[ 1-A[i], n-A[i] ]。如果C落在这个区间里,那么A[i]还是符合要求的。问题就变成找一个C,被覆盖的次数最多。
不改变和改变一次都好处理。我们分析一下改变两次怎么求。
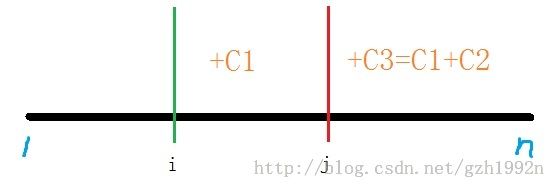
绿色线是第一次改变,红色是第二次(i<j)。记cnt[c,i]表示从i到n,c被覆盖的次数。sum[i]表示1到i符合条件的个数。
两次改变后,答案ans=cnt[c1,i]-cnt[c1,j]+cnt[c3,j]+sum[i-1]。
变换下顺序cnt[c1,i]+sum[i-1]+(cnt[c3,j]-cnt[c1,j])
如果i和c1确定了,那么cnt[c1,i]+sum[i-1]是固定部分,我们只要使得Max=(cnt[c3,j]-cnt[c1,j])的值最大化就好,至于j具体在哪里可以不管。
显然Max=max{max{cnt[c,j]} - cnt[c1,j]}(j>i)
从后往前推自然能得到每一个c1对应的Max,cnt[][]也不需要二维了。
维护更新每个c1的Max,用一个数组d[]记录。
复杂度O(n^2)
code:
#include <algorithm>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
#define N 3010
#define ll long long
#define ALL(x) x.begin(),x.end()
#define CLR(x,a) memset(x,a,sizeof(x))
typedef pair<int,int> PI;
const int INF=0x3fffffff;
const int MOD=1000000007;
const double EPS=1e-9;
/*----------------code-----------------*/
int cnt[N*3],d[N*3],a[N],sum[N];
int main(){
int n,Max,ans;
while(~scanf("%d",&n)){
ans=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
if(1<=a[i] && a[i]<=n) ans++;
sum[i]=ans;
}
CLR(cnt,0);
CLR(d,0);
Max=0;
for(int i=n;i>=1;i--){
for(int c=1-a[i];c<=n-a[i];c++) Max=max(Max,++cnt[c+n]);
for(int c=-n+1;c<=2*n;c++){
ans=max(ans,cnt[c+n]+sum[i-1]); //change once
ans=max(ans,cnt[c+n]+d[c+n]+sum[i-1]); //change twices
}
for(int c=-n+1;c<=2*n;c++) d[c+n]=max(d[c+n],Max-cnt[c+n]);
}
printf("%d\n",ans);
}
return 0;
}
ZOJ 3741 Eternal Reality
dp[i]表示前i-1轮已经完成,第i轮可以Level Upper,此时的最大值。用Max[i]表示在[i,i+x+y-1]这段区间内能获得的最大值(使用Level Upper或不使用)。sum[i]表示前i轮能获得的值。
转移:
dp[i]=max{ dp[j]+Max[j]+(sum[i]-sum[j+x+y-1]) | j+x+y-1<i }
所求的答案在dp[n+1],但是n+1这个位置比较特殊,它不需要要求第n+1轮可以Level Upper,因为他根本就不存在。
所以n+1的时候,转移的范围是j<=n
还有一个坑,就是LV5不能增加到LV6
code:
#include <algorithm>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
#define N 100100
#define ll long long
#define ALL(x) x.begin(),x.end()
#define CLR(x,a) memset(x,a,sizeof(x))
typedef pair<int,int> PI;
const int INF=0x3fffffff;
const int MOD=1000000007;
const double EPS=1e-9;
int a[N],dp[N],Max[N],sum[N];
int main(){
int L,n,x,y;
while(~scanf("%d%d%d%d",&L,&n,&x,&y)){
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
CLR(dp,0);
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+(a[i]<=L);
if(L<5) L++;
for(int i=1;i<=n;i++){
int tot=0;
for(int j=i;j<=min(n,i+x-1);j++) if(a[j]<=L) tot++;
for(int j=i+x;j<=min(n,i+x+y-1);j++) if(a[j]<=0) tot++;
Max[i]=max(tot,sum[min(n,i+x+y-1)]-sum[i-1]);
}
for(int i=1;i<=n;i++){
for(int j=1;j+x+y-1<i;j++)
dp[i]=max(dp[i],dp[j]+Max[j]+sum[i-1]-sum[j+x+y-1]);
dp[i]=max(dp[i],sum[i-1]);
}
int ans=0;
for(int i=1;i<=n;i++)
ans=max(ans,dp[i]+Max[i]+sum[n]-sum[min(n,i+x+y-1)]);
printf("%d\n",ans);
}
return 0;
}
ZOJ 3742 Bellywhite's Algorithm Homework
按点连的边数分为>sqrt(m)的和小于等于sqrt(m)的。
对于小的点,每次更新直接暴力每条边即可。
对于大的点,记录整数和与负数和,每次更新交换一下,同时要更新与它有交集的大的点。也就是说一开始还要预处理出2个大的点之间交集的整数和与负数和。
查询的话,记录一个全局的整数和与负数和,每次都能O(1)回答。
具体更新细节可以看代码。复杂度O(Qsqrt(m))。代码还有可以优化的地方,虽然有重边,但是两点之间可以压缩成两条边,正边,负边。
code:
#include <algorithm>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
#define N 50100
#define ll long long
#define ALL(x) x.begin(),x.end()
#define CLR(x,a) memset(x,a,sizeof(x))
typedef pair<int,int> PI;
const int INF=0x3fffffff;
const int MOD=1000000007;
const double EPS=1e-9;
int n,m,limit,num[N];
ll POS,NEG,pos[N],neg[N];
map<PI,pair<ll,ll> > crs;
vector<int> e[N],big;
struct Edge{
int u,v;
ll val;
}edge[N];
void change(int x){
if(e[x].size()>limit){
for(int i=0;i<big.size();i++){
int u=x,v=big[i];
if(u>v) swap(u,v);
map<PI,pair<ll,ll> >::iterator it;
if((it=crs.find(make_pair(u,v)))!=crs.end()){
v=big[i];
pair<ll,ll> &p=it->second;
pos[v]-=p.first, neg[v]-=p.second;
swap(p.first,p.second);
p.first=-p.first;
p.second=-p.second;
pos[v]+=p.first, neg[v]+=p.second;
}
}
POS-=pos[x], NEG-=neg[x];
swap(pos[x],neg[x]);
pos[x]=-pos[x];
neg[x]=-neg[x];
POS+=pos[x], NEG+=neg[x];
}else{
for(int i=0;i<e[x].size();i++){
int eid=e[x][i];
int u=edge[eid].u, v=edge[eid].v, val=edge[eid].val;
if(u!=x) swap(u,v);
if(e[v].size()>limit){
if(num[u]^num[v]) val=-val;
pos[v]-=val, neg[v]-=val;
}else{
edge[eid].val=-val;
}
POS-=val, NEG-=val;
}
}
num[x]^=1;
}
void pretreat(){
for(int i=1;i<=n;i++) if(e[i].size()>limit){
big.push_back(i);
}
for(int i=0;i<m;i++){
int u=edge[i].u, v=edge[i].v;
if(edge[i].val>0){
pos[u]+=edge[i].val;
pos[v]+=edge[i].val;
}else{
neg[u]+=edge[i].val;
neg[v]+=edge[i].val;
}
if(e[u].size()>limit && e[v].size()>limit){
if(u>v) swap(u,v);
if(edge[i].val>0)
crs[make_pair(u,v)].first+=edge[i].val;
else
crs[make_pair(u,v)].second+=edge[i].val;
}
}
}
void clear(){
big.clear();
crs.clear();
CLR(num,0);
CLR(pos,0);
CLR(neg,0);
for(int i=1;i<=n;i++) e[i].clear();
}
int main(){
int Q,x,Case=0;
while(~scanf("%d%d%d",&n,&m,&Q)){
if(Case++) puts("");
POS=0,NEG=0;
for(int i=0;i<m;i++){
scanf("%d%d%lld",&edge[i].u,&edge[i].v,&edge[i].val);
if(edge[i].val==0){
i--,m--;
continue;
}
e[edge[i].u].push_back(i);
e[edge[i].v].push_back(i);
if(edge[i].val>0) POS+=edge[i].val;
else NEG+=edge[i].val;
}
limit=sqrt(m)+1;
pretreat();
while(Q--){
char op[2];
scanf("%s",op);
if(op[0]=='Q'){
scanf("%s",op);
if(op[0]=='+') printf("%lld\n",POS);
else if(op[0]=='-') printf("%lld\n",NEG);
else printf("%lld\n",POS+NEG);
}else{
scanf("%d",&x);
change(x);
}
if(POS<0 || NEG>0) return -1;
}
clear();
}
return 0;
}
关键信息ri < li+1
那么直接暴力就好了,dp[i]记录i这个数有几个。
如果更新后的数字小于等于ri,那么这个数字就固定了,答案就加上它。
不过代码里我是全部更新好最后一起加的。
code:
#include <algorithm>
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <string>
#include <math.h>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
#define N 100100
#define ll long long
#define ALL(x) x.begin(),x.end()
#define CLR(x,a) memset(x,a,sizeof(x))
typedef pair<int,int> PI;
const int INF=0x3fffffff;
const int MOD=1000000007;
const double EPS=1e-9;
int dp[2*N];
int main(){
int n,m,x;
while(~scanf("%d%d",&n,&m)){
CLR(dp,0);
for(int i=0;i<n;i++){
scanf("%d",&x);
dp[x]++;
}
while(m--){
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
for(int i=r;i>=l;i--){
if(i+c>r) dp[i+c]+=dp[i];
else dp[i+c]=dp[i];
dp[i]=0;
}
}
ll ans=0;
for(int i=1;i<2*N;i++) ans+=1ll*dp[i]*i;
printf("%lld\n",ans);
}
return 0;
}