简与美(7)
脑中的数学是抽象的,手中的数学是简单的。
我们已经介绍了隐马模型,并且用动态规划思想解决了隐马模型提出的两个问题。尤其是第二个问题,和我们接下来要讨论的词性标注有直接关系。
在NPL领域,有一个称为N元模型的语言统计模型,它对应N-1阶马尔科夫模型。
N元模型可用于计算语句W=w1,w2,..,wn的先验概率P(W),在这里用变量W代表一个文本中顺序排列的n个词语。根据概率的乘法规则,P(W)可以分解为:
P(W)=P(w1)P(w2|w1)P(w3|w1,w2) .. P(wn|w1,w2,..,wn-1)
可见,为了预测wn的出现概率,必须要知道它前面所有词语的出现概率。w1,w2,..,wn-1被称为产生wn的历史。随着历史长度的增加,不同历史数按指数级增长。如果历史长度为i-1,则有
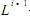 个不同的历史(L为词汇集的大小,还记得排列组合知识吧,这就是一个排列组合结果)。我们必须考虑在所有的 种历史的情况下,产生第i个词语的概率。也就是说,这样的模型中有 个自由参数P(wi|w1,w2,..,wi-1)。当L=5000,i=3时,自由参数的数目是1250亿。我们几乎不可能从训练数据中正确的估计这些参数,并且绝大多数的历史(排列组合)在训练数据中根本没有出现。解决这个问题的方法是将历史w1,w2,..,wi-1按照某个法则映射到等价类S(w1,w2,..,wi-1),而等价类的数目远远小于不同历史的数目。有很多方法可以将历史划分为等价类,比如,把参数空间中一些特征相近的元素合并到一起得到一个个等价类,于是,参加运算的是这些类,而不再是单个的元素。从计算角度看,这还是太复杂。如果任意一个词语出现的概率只和它前面的N-1个词语相关,那么问题可以得到进一步的简化。这时的语言模型叫做N元模型或N元语法(N-gram),即:
个不同的历史(L为词汇集的大小,还记得排列组合知识吧,这就是一个排列组合结果)。我们必须考虑在所有的 种历史的情况下,产生第i个词语的概率。也就是说,这样的模型中有 个自由参数P(wi|w1,w2,..,wi-1)。当L=5000,i=3时,自由参数的数目是1250亿。我们几乎不可能从训练数据中正确的估计这些参数,并且绝大多数的历史(排列组合)在训练数据中根本没有出现。解决这个问题的方法是将历史w1,w2,..,wi-1按照某个法则映射到等价类S(w1,w2,..,wi-1),而等价类的数目远远小于不同历史的数目。有很多方法可以将历史划分为等价类,比如,把参数空间中一些特征相近的元素合并到一起得到一个个等价类,于是,参加运算的是这些类,而不再是单个的元素。从计算角度看,这还是太复杂。如果任意一个词语出现的概率只和它前面的N-1个词语相关,那么问题可以得到进一步的简化。这时的语言模型叫做N元模型或N元语法(N-gram),即:
P(W)=P(w1)P(w2|w1)P(w3|w1,w2)..P(wi|wi-N+1,..,wi-1)
通常N的值不能太大,否则会有太多的等价类,前面提到的过多自由参数的问题仍然存在。当N=1时,即近似认为出现在第i位置上的词语wi独立于历史(它的出现概率跟它前面的词语无关),这种N元语言模型成为一元语法(uni-gram)。当N=2时,即近似认为出现在第i位置上的词语wi的出现概率只跟它前面紧邻的一个词语有关,这种N元语言模型称为二元语法(bi-gram)。当N=3时,即近似认为出现在第i位置上的词语wi的出现概率只跟它前面紧邻的两个词语有关。这种N元语言模型称为三元语法(tri-gram)。其实,N元模型就是N-1阶马尔科夫模型。因此,一元语法就是零阶马尔科夫链,二元语法就是一阶马尔科夫链,三元语法就是二阶马尔科夫链,...。当使用三元语法模型时,P(W) 可以分解为:
P(W)=P(w1)P(w2|w1)P(w3,|w1,w2)P(w4|w2,w3)..P(wi|wi-2,wi-1)
该模型的参数为P(w3|w2,w1),其值可以通过大规模语料库用最大似然估计方法求得:
P(w3|w2,w1)=f(w3|w2,w1)=count(w1,w2,w3)/count(w1,w2)
其中,count(w1,w2,w3)表示一个特定的词序列w1,w2,w3在语料库中出现的次数,count(w1,w2)表示一个特定的词序列w1,w2在语料库中出现的次数,f(w3|w2,w1)表示在给定w1,w2的条件下出现w3的概率。但是,在训练数据中,很可能事件w1,w2,w3这种词序列根本没有出现过,根据最大似然估计,这些事件的概率为零。然而,这些事件的真实概率不一定为零。这就是所谓的数据稀疏问题。这个问题有一些方法解决,比如遇到概率为零的时候给一个小的数值。
我们来看看词性标注问题。
词性标注问题可以看作是在给定词的序列W=w1,w2,..,wn的条件下,寻找一个词性标注序列C=c1,c2,..,cn使得P(C|W)最大。P(C|W)表示已知输入词序列W的情况下,出现词性标注序列C的条件概率。根据贝叶斯定律:
P(C|W)=P(W|C)P(C)/P(W)
P(W)是一个常数。可以忽略不计,则:
P(C|W)=P(W|C)P(C)
接着,对公式进行近似。首先,引入独立性假设,认为词序列中任意一个词wi的出现概率近似只跟当前词的词性标注ci有关,而跟上下文的词性标注无关。则词汇概率(某个词以某种词性出现的概率)为:
P(W|C)=P(w1|c1)P(w2|c2)..P(wn|cn)
显然,这是一种一元语法模型,它只考虑词跟在其上可能出现的词性标注之间的统计信息,即一个词用作某种词性的概率。其次,采用二元假设,认为任意词性标注ci的出现概率只跟它的紧邻的前一个词性标注ci+1相关,即:
P(C)=P(c2|c1)P(c3|c2)..P(cn|cn-1)
P(ci|ci-1)是词性标注的转移概率,显然这是一种二元语法模型,他只考虑词性一级上的相邻上下文关系(即某种词性序列是否出现的统计关系),但是没有考虑特定的词跟某种词性标注之间的统计关系(即一个词用作某种词性的概率)。现在公式为:
P(C|W)=P(w1|c1)P(c1|c0)..P(wi|ci)P(ci|ci-1)..P(wn|cn)P(cn|cn-1)
到目前为止,我们是用N元模型解释词性标注过程,仔细观察上面那个公式,我们要求的是使得P(C|W)取得最大值的C,这不就是一个隐马尔科夫模型嘛。模型中每个状态对应于一个词性标注,从状态Si(对应于词性标注ci)到状态Sj(对应于词性标注cj)的转移概率aij为相应的词性标注的二元语法模型P(cj|ci),从状态Si输出词语wi的发射概率bi(wi)为基于一元语法的词汇概率P(wi|ci)。于是,词性标注问题变为求隐马尔科夫模型的最佳状态序列的问题。用viterbi算法来解决。
另外,这个隐马尔科夫模型中的两个概率参数都可以通过训练数据来分别估计:
P(wi|ci)=count(wi,ci)/count(ci)
P(ci|ci-1)=count(ci-1,ci)/count(ci-1)
第一个公式说的是,词汇概率(发射概率)约等于训练数据中某个词语wi作某种词性ci使用的次数,除以该词性标注ci在训练数据中出现的总次数。第二个公式说的是,转移概率约等于训练数据中某种词性标注ci出现在另一种词性标注ci-1之后的次数,除以另一种词性标注ci-1在训练数据中出现的总次数。
我们通过介绍N元模型来说明词性标注的问题,并在最终把N元模型解释的问题转化为隐马尔科夫模型,并介绍了训练隐马参数的估计方法。到目前为止,中文分词系统涉及的大部分知识已经讲述差不多了。至于未登录词的识别问题,也是转化为隐马模型可以解决的问题来求解。后面有时间的时候会单独一篇来讨论。
本周开始,工作上会较以前忙一些,因为开始做一些确定的事情,这个系列会写的比较慢,并且我想把已经在之前讨论过的一些问题重新再认识一番,研究发现问题和解决问题的思路,并且发散思维,思考这些模型和方法能否举一反三用在其他技术领域。很值得思考。
待续...