组合数学

 

组合数学

(2011-10-09 18:00:55)

标签： 校园

分类： 工作篇

中国组合数学与图论学会 http://www.cscgt.org/index.htm

 

组合数学

组合数学（combinatorial mathematics），又称为离散数学。狭义的组合数学主要研究满足一定条件的组态（也称组合模型）的存在、计数以及构造等方面问题。组合数学主要内容有组合计数、组合设计、组合矩阵、组合优化等。有时人们也把组合数学和图论加在一起看作离散数学。组合数学是计算机出现以后迅速发展起来的一门数学分支。计算机科学即算法的科学，而计算机所处理的对象是离散的数据，所以离散对象的处理就成了计算机科学的核心，而研究离散对象的科学恰恰就是组合数学。组合数学的发展改变了传统数学中分析和代数占统治地位的局面。

简介

　　 现代数学可以分为两大类：一类是研究连续对象的，如分析、 方程 等，另一类就是研究离散对象的组合数学。组合数学不仅在 基础数学研究中具有极其重要的地位，在其它的学科中也有重要的应用，如计算机科学、编码和 密码学、物理、化学、生物等学科中均有重要应用。 微积分和近代数学的发展为近代的工业革命奠定了基础。而组合数学的发展则是奠定了本世纪的计算机革命的基础。计算机之所以可以被称为电脑，就是因为计算机被人编写了程序，而程序就是算法，在绝大多数情况下，计算机的算法是针对离散的对象，而不是在作数值计算。正是因为有了组合算法才使人感到，计算机好像是有思维的。 　　组合数学不仅在 软件技术中有重要的应用价值，在企业管理，交通规划，战争指挥，金融分析等领域都有重要的应用。在 美国有一家用组合数学命名的公司，他们用组合数学的方法来提高企业管理的效益，这家公司办得非常成功。此外，试验设计也是具有很大应用价值的学科，它的 数学原理就是组合设计。用组合设计的方法解决工业界中的试验设计问题，在美国已有专门的公司开发这方面的软件。

国外状况

　　组合数学在国外早已成为十分重要的学科，甚至可以说是计算机科学的基础。一些大公司，如IBM，AT&T都有全世界最强的组合研究中心。Microsoft 的Bill Gates近来也在提倡和支持计算机科学的基础研究。例如，Bell实验室的有关 线性规划算法的实现，以及有关计算机网络的算法，由于有明显的商业价值，显然是没有对外公开的。美国已经有一种趋势，就是与新的算法有关的软件是可以申请专利的。如果照这种趋势发展，世界各国对组合数学和 计算机算法的投入和竞争必然日趋激烈。美国政府也成立了离散数学及 理论计算机科学中心DIMACS（与Princeton大学，Rutgers大学，AT&T 联合创办的，设在Rutgers大学），该中心已是组合数学理论计算机科学的重要研究阵地。美国国家数学科学研究所（Mathematical Sciences Research Institute，由 陈省身先生创立）在1997年选择了组合数学作为研究专题，组织了为期一年的研究活动。 日本的NEC公司还在美国的设立了研究中心，理论计算机科学和组合数学已是他们重要的研究课题，该中心主任R. Tarjan即是组合数学的权威。美国重要的国家实际室（Los Alamos国家实验室，以造出第一颗原子弹著称于世），从 曼哈顿计划以来一直重视 应用数学的研究，包括组合数学的研究。不仅如此，该实验室最近还在积极充实组合数学方面的研究实力。美国另外一个重要的国家实验室Sandia国家实验室有一个专门研究组合数学和计算机科学的机构，主要从事组合编码理论和密码学的研究，在美国政府以及国际学术界都具有很高的地位。 　　由于 生物学中的DNA的结构和生物现象与组合数学有密切的联系，各国对生物信息学的研究都很重视，这也是组合数学可以发挥作用的一个重要领域。由于DNA就是组合数学中的一个序列结构， 美国科学院院士，近代组合数学的奠基人Rota教授预言，生物学中的 组合问题 将成为组合数学的一个前沿领域。 　　 传统的计算机算法可以分为两大类，一类是组合算法，一类是数值算法（包括 计算数学 和与处理各种信息数据有关的信息学）。近年来计算机算法又多了一类：那就是符号计算算法。吴文俊院士开创的 机器证明方法就属于符号计算，引起了国际上的高度评价，被称为吴方法。而国际上还有专门的符号计算杂志。符号算法和吴方法跟代数 组合学 也有十分密切的联系。 组合数学，数值计算（包括计算数学，科学计算，非线性科学，和与处理各种信息数据有关的信息学）和统计学可能是应用最广的数学分支，而组合数学的价值甚至不亚于统计学和数值计算。由于数学机械化近年来的发展和在计算机科学中的重要性，把数学机械化，科学计算和组合数学组合起来，就可以说是中国信息产业的基础。组合数学家H. Wilf和D. Zeilberger1998因为在组合恒等式的机械化证明方面的成果，获得1998年美国数学会的Steele奖。 　　Thomson Science公司创刊的一份电子刊物《离散数学和理论计算机科学》即是一个很好的说明。它的内容涉及离散数学和计算机科学的众多方面。由于计算机软件的促进和需求，组合数学已成为一门既广博又深奥的学科，需要很深的数学基础，逐渐成为了数学的主流分支。 　　除上述以外，欧洲也在积极发展组合数学， 英国、法国、德国、 荷兰、丹麦、奥地利、 瑞典、意大利、 西班牙等国家都建立了各种形式的组合数学研究中心。近几年，南美国家也在积极推动组合数学的研究。澳大利亚， 新西兰也组建了很强的组合数学研究机构。值得一提的是亚洲的 发达国家也十分重视组合数学的研究。日本有组合数学研究中心，并且从美国引进人才，不仅支持日本国内的研究，还出资支持美国的有关课题的研究，这样使日本的组合数学这几年的发展极为迅速。台湾、 香港两地也从美国引进人才，大力发展组合数学。新加坡， 韩国，马来西亚也在积极推动组合数学的研究和人才培养。台湾的数学研究中心也正在考虑把组合数学作为重点方向来发展。

花絮

四色问题

　　如果你仔细留心一张 世界地图，你会发现用一种颜色对一个国家着色，那么一共只需要四种颜色就能保证每两个相邻的国家的颜色不同。这样的着色效果能使每一个国家都能清楚地显示出来。但要证明这个结论确是一个著名的世界难题，1976年数学家通过计算机运算得到证明而成为 四色定理，最近人们才发现了一个更简单的证明。

中国邮差问题

　　由中国组合数学家 管梅谷教授提出。邮递员要穿过城市的每一条路至少一次，怎样行走走过的路程最短？这是一个 NP完全问题。由中国组合数学家管梅谷教授提出，著名组合数学家，J. Edmonds和他的合作者给出了一个解答。

任务分配问题（也称婚配问题）

　　有一些员工要完成一些任务。各个员工完成不同任务所花费的时间都不同。每个员工只分配一项任务。每项任务只被分配给一个员工。怎样分配员工与任务以使所花费的时间最少？

河洛图

　　我国古代的河洛图上记载了三阶幻方，即把从一到九这九个数按三行三列的队行排列，使得每行，每列，以及两条 对角线上的三个数之和都是一十五。组合数学中有许多象幻方这样精巧的结构。1977年美国旅行者1号、2号宇宙飞船就带上了幻方以作为人类智慧的信号。（题图）

装箱问题

　　当你装一个箱子时，你会发现要使箱子尽可能装满不是一件很容易的事，你往往需要做些调整。从理论上讲，装箱问题是一个很难的组合数学问题，即使用计算机也是不容易解决的。

过河问题

　　在中小学的 数学游戏中，有这样一个问题，一个船夫要把一只狼，一只羊和一棵白菜运过河。问题是当人不在场时，狼要吃羊，羊要吃白菜，而他的船每趟只能运其中的一个。他怎样才能把三者都运过河呢？这就是一个很典型、很简单的组合数学问题。

是否存在稳定婚姻的问题

　　假如能找到两对夫妇（如张（男）--李（女）和赵（男）--王（女）），如果张（男）更喜欢王（女），而王（女）也更喜欢张（男），那么这样就可能有潜在的不稳定性。组合数学的方法可以找到一种婚姻的安排方法，使得没有上述的不稳定情况出现（当然这只是理论上的结论）。这种组合数学的方法却有一个实际的用途：美国的医院在确定录取住院医生时，他们将考虑申请者的志愿的先后次序，同时也给申请排序。按这样的次序考虑出的总的方案将没有医院和申请者两者同时后悔的情况。实际上，高考学生的最后录取方案也可以用这种方法。

管理调度问题

　　我们还会遇到更复杂的调度和安排问题。例如，在生产原子弹的曼哈顿计划中，涉及到很多工序，许多人员的安排，很多元件的生产，怎样安排各种人员的工作，以及各种工序间的衔接，从而使整个工期的时间尽可能短？这些都是组合数学典型例子。又比如，假日饭店的管理中，也严格规定了有关的工序，如清洁工的第一步是换什么，清洗什么，第二步又做什么，总之，他进出房间的次数应该最少。既然，这样一个简单的工作都需要讲究工序，那么一个复杂的工程就更不用说了。

库房和运输的管理问题

　　怎样安排运输使得库房充分发挥作用，进一步来说，货物放在什么地方最便于存取（如存储时间短的应该放在容易存取的地方）。

铺地砖问题

　　我们知道，用形状相同的方型砖块可以把一个地面铺满（不考虑边缘的情况），但是如果用不同形状，而又非方型的砖块来铺一个地面，能否铺满呢？这不仅是一个与实际相关的问题，也涉及到很深的组合数学问题。

组合数学还可用于金融分析

　　◆组合数学还可用于金融分析，投资方案的确定，怎样找出好的投资组合以降低投资风险。南开大学组合数学研究中心开发出了"金沙股市风险分析系统"现已投放市场，为短线投资者提供了有效的风险防范工具。 　　总之，组合数学无处不在，它的主要应用就是在各种复杂关系中找出最优的方案。所以组合数学完全可以看成是一门量化的关系学，一门量化了的 运筹学，一门量化了的管理学。

扩展阅读：

• http://evilcat.bokee.com/4828065.html

• http://www.combinatorics.net.cn/

 

 

信息时代的组合数学

 

南开大学组合数学研究中心　陈永川

 

1. 组合数学概述

组合数学，又称为离散数学，但有时人们也把组合数学和图论加在一起算成是离散数学。组合数学是计算机出现以后迅速发展起来的一门数学分支。计算机科学就是算法的科学，而计算机所处理的对象是离散的数据，所以离散对象的处理就成了计算机科学的核心，而研究离散对象的科学恰恰就是组合数学。组合数学的发展改变了传统数学中分析和代数占统治地位的局面。现代数学可以分为两大类：一类是研究连续对象的，如分析、方程等，另一类就是研究离散对象的组合数学。组合数学不仅在基础数学研究中具有极其重要的地位，在其它的学科中也有重要的应用，如计算机科学、编码和密码学、物理、化学、生物等学科中均有重要应用。微积分和近代数学的发展为近代的工业革命奠定了基础。而组合数学的发展则是奠定了本世纪的计算机革命的基础。计算机之所以可以被称为电脑，就是因为计算机被人编写了程序，而程序就是算法，在绝大多数情况下，计算机的算法是针对离散的对象，而不是在作数值计算。正是因为有了组合算法才使人感到，计算机好象是有思维的。

组合数学不仅在软件技术中有重要的应用价值，在企业管理，交通规划，战争指挥，金融分析等领域都有重要的应用。在美国有一家用组合数学命名的公司，他们用组合数学的方法来提高企业管理的效益，这家公司办得非常成功。此外，试验设计也是具有很大应用价值的学科，它的数学原理就是组合设计。用组合设计的方法解决工业界中的试验设计问题，在美国已有专门的公司开发这方面的软件。最近，德国一位著名组合数学家利用组合数学方法研究药物结构，为制药公司节省了大量的费用，引起了制药业的关注。

在1997年11月的南开大学组合数学研究中心成立大会上，吴文俊院士指出，每个时代都有它特殊的要求，使得数学出现一个新的面貌，产生一些新的数学分支，组合数学这个新的分支也是在时代的要求下产生的。最近，吴文俊院士又指出，信息技术很可能会给数学本身带来一场根本性的变革，而组合数学则将显示出它的重要作用。杨乐院士也指出组合数学无论在应用上和理论上都具有越来越重要的位置，它今后的发展是很有生命力，很有前途的，中国应该倡导这个方面的研究工作。万哲先院士甚至举例说明了华罗庚，许宝禄，吴文俊等中国老一辈的数学家不仅重视组合数学，同时还对组合数学中的一些基本问题作了重大贡献。迫于中国组合数学发展自身的需要，以及中国信息产业发展的需要，在中国发展组合数学已经迫在眉睫，刻不容缓。

2. 组合数学与计算机软件

随着计算机网络的发展，计算机的使用已经影响到了人们的工作，生活，学习，社会活动以及商业活动，而计算机的应用根本上是通过软件来实现的。我在美国听到过一种说法，将来一个国家的经济实力可以直接从软件产业反映出来。我国在软件上的落后，要说出根本的原因可能并不是很简单的事，除了技术和科学上的原因外，可能还跟我们的文化，管理水平，教育水平，思想素质等诸多因素有关。除去这些人文因素以外，一个最根本的原因就是我国的信息技术的数学基础十分薄弱，这个问题不解决，我们就难成为软件强国。然而问题决不是这么简单，信息技术的发展已经涉及到了很深的数学知识，而数学本身也已经发展到了很深、很广的程度并不是单凭几个聪明的头脑去想想就行了，而更重要的是需要集体的合作和力量，就象软件的开发需要多方面的人员的合作。美国的软件之所以能领先，其关键就在于在数学基础上他们有很强的实力，有很多杰出的人才。一般人可能会认为数学是一门纯粹的基础科学，1+1的解决可能不会有任何实际的意义。如果真是这样，一门纯粹学科的发展落后几年，甚至十年，关系也不大。然而中国的软件产业的发展已向数学基础提出了急切的需求：网络算法和分析，信息压缩，网络安全，编码技术，系统软件，并行算法，数学机械化和计算机推理，等等。此外，与实际应用有关的还有许多许多需要数学基础的算法，如运筹规划，金融工程，计算机辅助设计等。如果我们的软件产业还是把眼光一直盯在应用软件和第二次开发，那么我们在应用软件这个领域也会让国外的企业抢去很大的市场。如果我们现在在信息技术的数学基础上，大力支持和投入，那将是亡羊补牢，犹未为晚；只要我们能抢回信息技术的数学基地，那么我们还有可能在软件产业的竞争中，扭转局面，甚至反败为胜。吴文俊院士开创和领导的数学机械化研究，为中国在信息技术领域占领了一个重要的阵地，有了雄厚的数学基础，自然就有了软件开发的竞争力。这样的阵地多几个，我们的软件产业就会产生新的局面。值得注意的是，印度有很好的统计和组合数学基础，这可能也是印度的软件产业近几年有很大发展的原因。

3. 组合数学在国外的状况

纵观全世界软件产业的情况，易见一个奇特的现象：美国处于绝对的垄断地位。造成这种现象的一个根本的原因就是计算机科学在美国的飞速发展。当今计算机科学界的最权威人士很多都是研究组合数学出身的。美国最重要的计算机科学系（MIT，Princeton，Stanford，Harvard，Yale，….）都有第一流的组合数学家。计算机科学通过对软件产业的促进，带来了巨大的效益，这已是不争之事实。组合数学在国外早已成为十分重要的学科，甚至可以说是计算机科学的基础。一些大公司，如IBM，AT&T都有全世界最强的组合研究中心。Microsoft 的Bill Gates近来也在提倡和支持计算机科学的基础研究。例如，Bell实验室的有关线性规划算法的实现，以及有关计算机网络的算法，由于有明显的商业价值，显然是没有对外公开的。美国已经有一种趋势，就是与新的算法有关的软件是可以申请专利的。如果照这种趋势发展，世界各国对组合数学和计算机算法的投入和竞争必然日趋激烈。美国政府也成立了离散数学及理论计算机科学中心DIMACS（与Princeton大学，Rutgers大学，AT&T 联合创办的，设在Rutgers大学），该中心已是组合数学理论计算机科学的重要研究阵地。美国国家数学科学研究所（Mathematical Sciences Research Institute，由陈省身先生创立）在1997年选择了组合数学作为研究专题，组织了为期一年的研究活动。日本的NEC公司还在美国的设立了研究中心，理论计算机科学和组合数学已是他们重要的研究课题，该中心主任R. Tarjan即是组合数学的权威。我所熟悉的美国重要的国家实际室（Los Alamos国家实验室，以造出第一颗原子弹著称于世），从曼哈顿计划以来一直重视应用数学的研究，包括组合数学的研究。我所接触到的有关组合数学的计算机模拟项目经费达三千万美元。不仅如此，该实验室最近还在积极充实组合数学方面的研究实力。美国另外一个重要的国家实验室Sandia国家实验室有一个专门研究组合数学和计算机科学的机构，主要从事组合编码理论和密码学的研究，在美国政府以及国际学术界都具有很高的地位。由于生物学中的DNA的结构和生物现象与组合数学有密切的联系，各国对生物信息学的研究都很重视，这也是组合数学可以发挥作用的一个重要领域。前不久召开的北京香山会议就体现了国家对生物信息学的高度重视。据说IBM也将成立一个生物信息学研究中心。由于DNA就是组合数学中的一个序列结构，美国科学院院士，近代组合数学的奠基人Rota教授预言，生物学中的组合问题将成为组合数学的一个前沿领域。

美国的大学，国家研究机构，工业界，军方和情报部门都有许多组合数学的研究中心，在研究上投入了大量的经费。但他们得到的收益远远超过了他们的投入，更主要的是他们还聚集了组合数学领域全世界最优秀的人才。高层次的软件产品处处用到组合数学，更确切地说就是组合算法。传统的计算机算法可以分为两大类，一类是组合算法，一类是数值算法（包括计算数学和与处理各种信息数据有关的信息学）。依我个人的浅见，近年来计算机算法又多了一类：那就是符号计算算法。吴文俊院士开创的机器证明方法就属于符号计算，引起了国际上的高度评价，被称为吴方法。而国际上还有专门的符号计算杂志。符号算法和吴方法跟代数组合学也有十分密切的联系。组合数学，数值计算（包括计算数学，科学计算，非线性科学，和与处理各种信息数据有关的信息学）和统计学可能是应用最广的数学分支，而组合数学的价值甚至不亚于统计学和数值计算。由于数学机械化近年来的发展和在计算机科学中的重要性，把数学机械化，科学计算和组合数学组合起来，就可以说是中国信息产业的基础。组合数学家H. Wilf和D. Zeilberger1998因为在组合恒等式的机械化证明方面的成果，获得1998年美国数学会的Steele奖。

Gian-Carlo Rota教授在他去年不幸逝世之前，还专门向我提出，希望我向中国有关部门和领导人呼吁，组合数学是计算机软件产业的基础，中国最终一定能成为一个软件大国，但是要实现这个目标的一个突破点就是发展组合数学。中国在软件技术上远远落后于美国，而在组合数学上则更是落后于美国和欧洲。如果中国只是想在软件技术上跟着西方走，而不在组合数学上下功夫，那么中国的软件将一直处于落后的状态。他特别强调组合数学在计算机科学中的作用，以及在大学计算机系加强组合数学教学和人才培养。

最近Thomson Science公司创刊的一份电子刊物《离散数学和理论计算机科学》即是一个很好的说明。它的内容涉及离散数学和计算机科学的众多方面。由于计算机软件的促进和需求，组合数学已成为一门既广博又深奥的学科，需要很深的数学基础，逐渐成为了数学的主流分支。本世纪公认的伟大数学家盖尔芳德预言组合数学和几何学将是下一世纪数学研究的前沿阵地。这一观点不仅得到国际数学界的赞同，也得到了中国数学界的赞同和响应。

加拿大在Montreal成立了试验数学研究中心，他们的思路可能和吴文俊院士的数学机械化研究中心的发展思路类似，使数学机械化，算法化，不仅使数学为计算机科学服务，同时也使计算机为数学研究服务。吴文俊院士指出，中国传统数学中本身就有浓厚的算法思想。

今后的计算机要向更加智能化的方向发展，其出路仍然是数学的算法，和数学的机械化。另外的一个有说服力的现象是，组合数学家总是可以在大学的计算机系或者在计算机公司找到很好的工作，一个优秀的组合数学家自然就是一个优秀的计算机科学家。相反，美国所有大学计算机系都有组合数学的课程。

除上述以外，欧洲也在积极发展组合数学，英国、法国、德国、荷兰、丹麦、奥地利、瑞典、意大利、西班牙等国家都建立了各种形式的组合数学研究中心。近几年，南美国家也在积极推动组合数学的研究。澳大利亚，新西兰也组建了很强的组合数学研究机构。值得一提的是亚洲的发达国家也十分重视组合数学的研究。日本有组合数学研究中心，并且从美国引进人才，不仅支持日本国内的研究，还出资支持美国的有关课题的研究，这样使日本的组合数学这几年的发展极为迅速。台湾、香港两地也从美国引进人才，大力发展组合数学。新加坡，韩国，马来西亚也在积极推动组合数学的研究和人才培养。台湾的数学研究中心也正在考虑把组合数学作为重点方向来发展。世界各地对组合数学的如此钟爱显然是有原因的，那就是没有组合数学就没有计算机科学，没有计算机软件。

4. 组合数学花絮

** 在日常生活中我们常常遇到组合数学的问题。如果你仔细留心一张世界地图，你会发现用一种颜色对一个国家着色，那么一共只需要四种颜色就能保证每两个相邻的国家的颜色不同。这样的着色效果能使每一个国家都能清楚地显示出来。但要证明这个结论确是一个著名的世界难题，最终借助计算机才得以解决，最近人们才发现了一个更简单的证明。

** 我国古代的河洛图上记载了三阶幻方，即把从一到九这九个数按三行三列的队行排列，使得每行，每列，以及两条对角线上的三个数之和都是一十五。组合数学中有许多象幻方这样精巧的结构。1977年美国旅行者1号、2号宇宙飞船就带上了幻方以作为人类智慧的信号。

** 当你装一个箱子时，你会发现要使箱子尽可能装满不是一件很容易的事，你往往需要做些调整。从理论上讲，装箱问题是一个很难的组合数学问题，即使用计算机也是不容易解决的。

** 在中小学的数学游戏中，有这样一个问题，一个船夫要把一只狼，一只羊和一棵白菜运过河。问题是当人不在场时，狼要吃羊，羊要吃白菜，而他的船每趟只能运其中的一个。他怎样才能把三者都运过河呢？这就是一个很典型、很简单的组合数学问题。

** 我们还会遇到更复杂的调度和安排问题。例如，在生产原子弹的曼哈顿计划中，涉及到很多工序，许多人员的安排，很多元件的生产，怎样安排各种人员的工作，以及各种工序间的衔接，从而使整个工期的时间尽可能短？这些都是组合数学典型例子。

** 航空调度和航班的设定也是组合数学的问题。怎样确定各个航班以满足不同旅客转机的需要，同时也使得每个机场的航班起落分布合理。此外，在一些航班有延误等特殊情况下，怎样作最合理的调整，这些都是组合数学的问题。

** 对于城市的交通管理，交通规划，哪些地方可能是阻塞要地，哪些地方应该设单行道，立交桥建在哪里最合适，红绿灯怎样设定最合理，如此等等，全是组合数学的问题。

** 一个邮递员从邮局出发，要走完他所管辖的街道，他应该怎样选择什么样的路径，这就是著名的"中国邮递员问题"，由中国组合数学家管梅谷教授提出，著名组合数学家，J. Edmonds和他的合作者给出了一个解答。

** 一个通讯网络怎样布局最节省？美国的贝尔实验室和IBM公司都有世界一流的组合数学家在研究这个问题，这个问题直接关系到巨大的经济利益。

** 据说，假日饭店的管理中，也严格规定了有关的工序，如清洁工的第一步是换什么，清洗什么，第二步又做什么，总之，他进出房间的次数应该最少。既然，这样一个简单的工作都需要讲究工序，那么一个复杂的工程就更不用说了。

** 库房和运输的管理也是典型的组合数学问题。怎样安排运输使得库房充分发挥作用，进一步来说，货物放在什么地方最便于存取（如存储时间短的应该放在容易存取的地方）。

** 我们知道，用形状相同的方型砖块可以把一个地面铺满（不考虑边缘的情况），但是如果用不同形状，而又非方型的砖块来铺一个地面，能否铺满呢？这不仅是一个与实际相关的问题，也涉及到很深的组合数学问题。

** 组合数学中有一个著名问题：是否存在稳定婚姻的问题。假如能找到两对夫妇（如张（男）--李（女）和赵（男）--王（女）），如果张（男）更喜欢王（女），而王（女）也更喜欢张（男），那么这样就可能有潜在的不稳定性。组合数学的方法可以找到一种婚姻的安排方法，使得没有上述的不稳定情况出现（当然这只是理论上的结论）。这种组合数学的方法却有一个实际的用途：美国的医院在确定录取住院医生时，他们将考虑申请者的志愿的先后次序，同时也给申请排序。按这样的次序考虑出的总的方案将没有医院和申请者两者同时后悔的情况。实际上，高考学生的最后录取方案也可以用这种方法。

** 组合数学还可用于金融分析，投资方案的确定，怎样找出好的投资组合以降低投资风险。南开大学组合数学研究中心开发出了"金沙股市风险分析系统"现已投放市场，为短线投资者提供了有效的风险防范工具。

总之，组合数学无处不在，它的主要应用就是在各种复杂关系中找出最优的方案。所以组合数学完全可以看成是一门量化的关系学，一门量化了的运筹学，一门量化了的管理学。

胡锦涛同志在1998年接见"五四"青年奖章时发表的讲话中指出，组合数学不同于传统的纯数学的一个分支，它还是一门应用学科，一门交叉学科。他希望中国的组合数学研究能够为国家的经济建设服务。

如果21世纪是信息社会的世纪，那么21世纪也必将是组合数学大有可为的世纪。

有关组合数学的更进一步的资料可在南开大学组合数学研究中心的网页上找到：

http://www.combinatorics.net.cn/

http://www.combinatorics.net/cfc/

http://zikao.xjzsks.com/707/2005/212005031656.shtml

http://blog.csdn.net/bufferedreader/article/details/297313

http://wenku.baidu.com/view/d0bc7b1dc281e53a5802ffeb.html
http://zhidao.baidu.com/question/56342558.html

 

 

生活中矩阵的应用

摘要：矩阵作为一种重要的工具，在生活的方方面面都存在应用。比如科学地选彩票号码，图形的变换处理，控制监控系统都存在了矩阵的痕迹。矩阵在各个领域的应用为我们展示了矩阵的广泛实用性。矩阵实现了对组合的优化，对质量的管理优化，会变得越来越重要。

一．矩阵的概念
在开始讨论矩阵应用前，先了解一下矩阵及相关的一些概念。在数学上，矩阵是指纵横排列的二维数据表格，最早来自于方程组的系数及常数所构成的方阵，这一概念由19世纪英国数学家凯利首先提出。一些矩阵在农业，经济，通信等领域都存在许多特别的应用。
二．矩阵的特别的应用
  1．矩阵应用在选彩票号码
一些彩民由于未了解“旋转矩阵”的作用，都采取旧式的复式投注方式(即完全复式)，完完整整地拿去打彩，一些对复式投注进行深入研究的彩民发现进行复式投注浪费了不少成本。据研究者发现约有三分之一号码组合，实际上是不可能中奖或极难中奖的。
据说在美国彩票史上，Gail Howard运用一种叫做“旋转矩阵”投注选号法，奇迹般地中出了74个大奖。这种“旋转矩阵”法，是一种基于“旋转矩阵”数学原理构造的选号法，其核心是：以极低的成本实现复式投注的效果。
那么如何以极低的成本实现复式投注的最佳效果呢？这是由“旋转矩阵”法优点决定的。
实际上，旋转矩阵是教你如何科学地组合号码。与完全复式投注组合号码的方法相比，旋转矩阵有着投入低、中奖保证高的优点。
举个例子讲，10个号码的中6保5型的旋转矩阵的含义就是，你选择了10个号码，如果其中包含了6个中奖号码，那么运用该矩阵提供的14注号码，你至少有一注中对5个号码的奖。本矩阵只要投入28元，而相应的复式投注需要投入420元。大家知道，用10个号码，只购买其中的14注，如果你胡乱组合的话，即使这10个号码中包含有6个中奖号码，你也很可能只中得一些小奖。而运用旋转矩阵的话，就可以得到一个对5个号码的奖的最低中奖保证。　旋转矩阵是世界上著名的彩票专家、澳大利亚数学家底特罗夫研究的，它可以帮助您锁定喜爱的号码，提高中奖的机会。首先您要先选一些号码，然后，运用某一种旋转矩阵，将你挑选的数字填入相应位置。如果您选择的数字中有一些与开奖号码一样，您将一定会中一定奖级的奖。当然运用这种旋转矩阵，可以最小的成本获得最大的收益，且远远小于复式投注的成本。（1）
　　旋转矩阵的原理在数学上涉及到的是一种组合设计：覆盖设计。而覆盖设计，填装设计，斯坦纳系，t-设计都是离散数学中的组合优化问题。

2．矩阵在透视投影应用
　　三维计算机图形学中另外一种重要的变换是透视投影。与平行投影沿着平行线将物体投影到图像平面上不同，透视投影按照从投影中心这一点发出的直线将物体投影到图像平面。这就意味着距离投影中心越远投影越小，距离越近投影越大。
　　最简单的透视投影将投影中心作为坐标原点，z = 1 作为图像平面，这样投影变换为 x' = x / z; y' = y / z，用齐次坐标表示为：这个乘法的计算结果是 (xc,yc,zc,wc) = (x,y,z,z)。
　　在进行乘法计算之后，通常齐次元素 wc 并不为 1，所以为了映射回真实平面需要进行齐次除法，即每个元素都除以 wc：
　　更加复杂的透视投影可以是与旋转、缩放、平移、切变等组合在一起对图像进行变换。
比如给定n个点，m个操作，构造O(m+n)的算法输出m个操作后各点的位置。操作有平移、缩放、翻转和旋转这里的操作是对所有点同时进行的。其中翻转是以坐标轴为对称轴进行翻转（两种情况），旋转则以原点为中心。如果对每个点分别进行模拟，那么m个操作总共耗时O(mn)。利用矩阵乘法可以在O(m)的时间里把所有操作合并为一个矩阵，然后每个点与该矩阵相乘即可直接得出最终该点的位置，总共耗时O(m+n)。假设初始时某个点的坐标为x和y，下面5个矩阵可以分别对其进行平移、旋转、翻转和旋转操作。预先把所有m个操作所对应的矩阵全部乘起来，再乘以(x,y,1)，即可一步得出最终点的位置。

3．矩阵在质量问题中的运用
    矩阵是从多维问题的事件中，找出成对的因素，排列成矩阵图，然后根据矩阵图来分析问题，确定关键点的方法，它是一种通过多因素综合思考，探索问题的好方法。
　在复杂的质量问题中，往往存在许多成对的质量因素．将这些成对因素找出来，分别排列成行和列，其交点就是其相互关联的程度，在此基础上再找出存在的问题及问题的形态，从而找到解决问题的思路。
　　矩阵图的形式：A为某一个因素群，a1、a2、a3、a4、…是属于A这个因素群的具体因素，将它们排列成行；B为另一个因素群，b1、b2、b3、b4、…为属于B这个因素群的具体因素，将它们排列成列；行和列的交点表示A和B各因素之间的关系。按照交点上行和列因素是否相关联及其关联程度的大小，可以从中得到解决问题的启示。
　　质量管理中所使用的矩阵图，其成对因素往往是要着重分析的质量问题的两个侧面，如生产过程中出现了不合格品时，着重需要分析不合格的现象和不合格的原因之间的关系，为此，需要把所有缺陷形式和造成这些缺陷的原因都罗列出来，逐一分析具体现象与具体原因之间的关系，这些具体现象和具体原因分别构成矩阵图中的行元素和列元素。
　  矩阵图法的用途十分广泛．在质量管理中，常用矩阵图法解决以下问题：
　　①把系列产品的硬件功能和软件功能相对应，从中找出研制新产品或改进老产品的切入点，进行多变量分析、研究从何处入手以及以什么方式收集数据。
　　②明确应保证产品质量特性及与管理机构或保证部门的关系，使质量保证体制更可靠；
　　③当生产工序中存在多种不良现象，且它们具有若干个共同的原因时，搞清这些不良现象及其产生原因的相互关系，进而把这些不良现象一举消除。
　　④明确产品的质量特性与试验测定仪器、试验测定项目之间的关系，力求强化质量评价体制或使之提高效率；（2）

三，对矩阵应用的感悟
 上述的矩阵应用说明了矩阵不仅仅是解方程组的工具，而且它是一种有用的工具，不仅仅在数学领域，还在经济，计算机领域等领域。相信在不久的未来，矩阵会变得越来越重要。矩阵的作用会越来越多地让人们发现。在线性代数数学书中，方程组可以转换为矩阵，再通过矩阵来简单，快速地解决问题。在质量管理问题上，它采用矩阵图来找出切入点，了解原因，使质量效率提高。
 相信在不久的未来，矩阵对于优化问题的应用会越来越广泛，触及面会越来越多。矩阵是生活变得更简单，方便。

参考文献：
[1] 《科学通报》蒋昌俊,吴哲辉..,1989.
[2] 求解约束矩阵方程及其最佳逼近的迭代法的研究彭亚新.湖南大学,2005.

 

 

 

 

http://dimacs.fzu.edu.cn/type.asp?typeID=12

福州大学“离散数学与理论计算机科学研究中心”

 

 在迅速发展的计算机科学技术及信息技术等领域，离散数学是重要的基础学科和支撑学科，它的发展和应用是影响一个国家科学技术发展水平的重要因素。以福州大学“离散数学与理论计算机科学研究中心”为依托的离散数学及其应用教育部重点实验室于2007年7月获教育部批准立项建设。目前，实验室共有固定研究人员27人，其中教授15人，副教授5人，具有博士学位15人，从国外学成归来7人。实验室由马志明院士担任学术委员会主任，范更华教授担任实验室主任。

      实验室现有三个研究方向：图论与组合数学、大规模集成电路设计中的数学方法、优化理论与算法。近年来，实验室先后承担国家重点基础研究发展计划（973计划）课题1项、国家自然科学基金重点项目2项、国家自然科学基金项目14项。获国家自然科学二等奖1项，教育部科技一等奖1项，教育部科技二等奖1项。

      实验室不仅是高水平科学研究中心，也是高层次人才培养基地。实验室以应用数学、计算机应用技术省级重点学科，国家集成电路人才培养基地，离散数学“211工程”建设重点学科，应用数学博士点以及两个一级学科硕士点（数学、计算机科学与技术）为支撑，形成具有一定规模的离散数学高层次人才培养体系。实验室将充分利用自身的条件，围绕主攻方向，提升开放层次，促进学术交流与合作，使实验室整体研究水平达到国内领先水平，某些研究方向达到国际先进水平，为国家及福建地方建设做出突出贡献。

研究人员
·	宝   升	Bau Sheng,	教    授,  博  士	[email protected]
·	鲍学文	Bao Xuewen,	副教授,  博  士	[email protected]
·	常   安	Chang An,	教    授,  博  士	[email protected]
·	陈国龙	Chen Guolong,	教    授,  博  士	[email protected]
·	陈   容	Chen Rong,	讲    师,  博  士	[email protected]
·	陈荣斯	Chen Rongsi,	教    授,  博  士	[email protected]
·	范更华	Fan Genghua,	教    授,  博  士	[email protected]
·	侯建锋	Hou Jianfeng,	讲    师,  博  士	[email protected]
·	杨大庆	Yang Daqing,	副教授,  博  士	[email protected]
·	游天童	You Tiantong,	教    授,  博  士	[email protected]
·	周垂香	Zhou Chuixiang,	讲    师,  博  士	[email protected]
·	朱文兴	Zhu Wenxing,	教    授,  博  士	[email protected]

 

 

 

 

http://www.combinatorics.net.cn/introduction/index.htm#research

http://www.combinatorics.net.cn/

南开大学组合数学中心

南开大学组合数学中心由陈永川教授创建成立于1997年。在教育部、科技部、国家自然科学基金委、天津市和南开大学的大力支持和关心下，中心不断发展壮大，迅速成为具有国际影响的组合数学研究机构，现拥有“应用数学”国家重点学科、“核心数学与组合数学”教育部重点实验室、天津市“组合数学”重点实验室、“组合数学”教育部创新团队。

经过十余年的努力，南开大学组合数学中心已逐步发展成为包括固定人员、博士后、访问学者以及研究生在内的理论研究和人才培养基地。中心由获得联合国教科文组织青年科学家奖和中国五四青年奖章的陈永川教授担任主任。编辑部设在中心的国际刊物《Annals of Combinatorics》（《组合年刊》）2004年起被SCIE检索，2009年影响因子上升为0.679，在施普林格出版社进行的国际通讯评议中被评为“高质量（top quality）”的刊物，已经在国际组合数学界产生了很大的影响。这一刊物已经成为中国组合数学的一个重要学术阵地。

组合数学中心采取开放流动的教学和研究体制，每年都吸引众多国内外知名学者到访，形成了浓厚的学术交流氛围。美国著名科学家James D. Louck现为中心名誉主任，在国际学术界具有广泛影响的Alain Lascoux 教授（法国）、Xavier Viennot教授（法国）等受聘为中心兼职教授。美国科学院院士R. Askey教授、美国数学会前任会长、美国科学院院士G. Andrews教授，南开大学名誉教授、美国科学院院士R. Stanley教授都曾来中心做短期访问。中心成立以来成功举办大型国际会议7次，其中2004年的组合学术年以及两次国际会议的成功召开为中心的交流合作开创了新局面。2007年7月举办的第19届“形式幂级数与代数组合”国际年会是代数组合界最有影响的国际会议，也是开办19年来首次在亚洲举行。这次会议为来自19个国家和地区的80余所高校和科研机构的200多位专家学者提供了广泛的交流平台，在学术界产生了重大影响。

领导的支持和关怀

组合数学中心的成立和发展离不开各级领导的关怀和支持。1997年，著名数学家吴文俊院士、杨乐院士、万哲先院士、林群院士等参加了南开大学组合数学中心成立大会，对中心的发展给予了殷切的希望。1998年10月，李岚清副总理亲临中心，对中心的发展方向给予了指示和关心。2005年2月，全国人大常委会副委员长、九三学社中央主席韩启德院士视察组合数学中心，高度评价了组合数学中心取得的成绩。原国家教育部朱开轩部长、陈至立部长非常关心组合数学中心的成立。国家科技部程津培副部长和天津市政协主席邢元敏同志都曾亲临视察，对组合数学中心的建设和发展给予了宝贵的指导。

理论研究

中心近五年来已接受发表论文300余篇，其中大多数发表在本专业最高级别的刊物上，研究内容涉及组合数学、组合数学与计算机软件、图论与组合最优化、组合数论、计算生物学、概率组合论等领域。中心的科研成绩得到了国内外数学界的高度评价。国际数学大师陈省身先生多次参观中心，并称赞中心“办得很好，很先进”。A. Lascoux教授很有感触地说，“南开组合数学研究中心的发展，比当年法国组合数学学派的发展还快。”2003年，美国科学院院士G. Andrews在给南开大学的一封信中提到“我深知南开有一个很强的组合数学团队”。2004年，德国著名数学家A. Dress教授表示：“南开的组合数学中心已经很强了。”南开大学名誉教授、美国科学院院士 R. Stanley评价说：“南开大学组合数学中心取得了令人瞩目的成绩，其发展速度实在令人惊讶！”机器证明领域的著名数学家D. Zeilberger教授认为：“你们真的在中国建立了一个组合数学王国。”2004年，美国洛斯阿拉莫斯国家实验室计算机模拟研究部主任C. L. Barrett博士来到南开大学赞叹到：“南开已经是组合数学研究的一个世界中心。”2007年，国际数学化学科学院院士Ivan Gutman教授称赞道：“组合数学中心是国际上规模最大最优秀的研究中心之一，这里做出了非常强的科研工作。这一点不仅能在访问中心的时候了解到，还可以从中心在很多杂志上发表的论文中看出。中心产出的成果世界知名，论文都发表在国际主要的数学刊物上。你甚至不用到这里来就可以了解到中心是一个绝佳的作研究的地方。”

 

组合数学中心由获得联合国教科文组织“侯赛因”青年科学家奖的组合数学家陈永川教授担任主任，荟萃了国内外组合数学界的一批优秀的青年学者，其中包括教育部长江学者特聘教授陈永川，国际数学化学科学院院士李学良教授，国际知名组合数论学者高维东教授，教育部新世纪优秀人才侯庆虎教授等。中心本着“取天下名师，集域内英才”的办学宗旨，逐步发展成为包括特聘教授、教授、副教授、博士后、访问学者和博士、硕士研究生在内的理论研究和人才培养基地。 著名数学家吴文俊院士、杨乐院士、万哲先院士、林群院士等时常关心组合数学中心的发展。吴文俊院士指出，每一个时代都有它自己的数学，而组合数学就是信息时代所需要的数学。国际数学大师陈省身先生多次参观组合数学中心，并称赞中心“办得很好，很先进”，“对南开数学充满信心”。 组合数学中心浓厚的学术气氛和活跃的学术交流也吸引了国际上一流的专家和学者。美国科学院院士George Andrews教授说：“南开大学有一个很强的组合数学团队。”世界著名生物信息学家，Michael Waterman院士对中心的发展非常赞赏，他说：“组合数学对于生物信息学非常重要，基于中心成立以来的发展势头，我完全相信中心将在交叉学科的研究领域获得突出的成就。”南开大学名誉教授，美国科学院院士Richard Stanley在组合数学中心举办的国际会议上表示，组合数学中心取得了令人瞩目的成绩，其发展速度实在令人惊讶，有潜力成为国际上最有影响的组合数学研究中心之一。

 

http://www.math.nankai.edu.cn/mathlab/chinese/xsdw.html

南开大学核心数学与组合数学实验室

 

南开大学核心数学与组合数学实验室是2000年8月被教育部批准建设的重点开放实验室，于2000年9月正式对外开放。它所依托的南开大学现有基础数学、概率统计和应用数学三个国家重点学科。这些学科历史悠久，学风严谨，长期以来为国家的科学研究与教育事业做出了重大贡献，特别在微分几何、李群李代数、代数拓扑、概率统计、信息论等领域，有具备深厚基础的教学科研队伍，近年来又在非线性分析、组合数学、整体微分几何、算法信息论与编码理论、信号处理等领域有了很大的发展，总体水平居国内高校前列，其中许多研究成果已达到国际先进或领先水平。

    本实验室的学术研究立足于基础数学、概率统计为代表的核心数学和组合数学位代表的应用数学。目标是发展基础学科，促进核心数学和组合数学学科的理论研究和应用研究，通过交流合作扩大在国际上的影响。实验室的主要研究方向为：基础数学、组合数学与应用数学、信息科学。

    实验室主任为陈永川教授，学术委员会主任为龙以明教授。现有科研人员39名，其中有教授33名（包括博士生导师29名），副教授1名，讲师1名；有技术人员3名。其中，第三世界科学院院士1人、教育部“长江奖励计划”特聘教授5人、国家杰出青年基金获得者3人、跨世纪优秀人才基金获得者4人。

    本实验室每年举办大量高水平数学科研活动，与国内外知名学府和相关专业数学家建立了广泛的联系。这些学术会议、研讨班、系列讲座邀请许多国内外著名数学家来南开讲学，促进了国内与国际数学界的学术交流。同时，对外开放体制吸收多位国内外知名学者作为特聘讲座教授来实验室从事教学、科研工作。

  

1． 基础数学     基础数学侧重于基础理论研究，主要方向包括：整体微分几何，非线性分析，李群李代数，微分拓扑与代数拓扑、泛函分析等。     此方向主要研究人员有：张伟平、龙以明、方复全、孟道骥、侯自新、林金坤、定光桂、梁科、刘春根、扶磊、邓少强、吴志强、张震球教授和年青副教授与科研教学人员。 2．组合数学与应用数学     主要研究方向包括：代数组合学，计数组合学，组合数学机械化，图论算法，密码和编码，数据分析，图像处理、细胞自动机、偏微分方程及其应用、偏微分方程的数值分析方法、微分几何与控制论等。     此方向主要研究人员有：万哲先院士、陈永川、陈志敏、胡健伟、李学良、王红教授和年青副教授与科研教学人员。 3． 信息科学     主要研究方向包括：信息论基础理论，编码与密码学，非线性滤波和小波分析、概率论与数理统计、风险分析等。     此方向主要研究人员有：沈世镒、周性伟、符方伟、吴荣、张润楚、王永进、郭军义、王兆军、孙文昌教授和年青副教授与科研教学人员。

http://www.math.pku.edu.cn:8000/html/research/institution/mathlab/

http://www.lmam.pku.edu.cn/

北京大学“数学及其应用”教育部重点实验室

 

北京大学“数学及其应用”教育部重点实验室是作为世界银行贷款“重点学科发展项目”于1989年建立的。1994年成为国家教委重点开放实验室，1995年通过了国家教委世界银行贷款项目专家组对实验室的验收检查；2000年被准予参加国家实验室评估，被评为国家A级重点实验室，名列当年数理口第三。2004.10-11参加教育部重点实验室的评估，再次被评为优秀。

　　自实验室成立以来，在国家科技部、教育部和北京大学的领导和大力支持下，北京大学“数学及其应用”实验室根据世界数学发展潮流，瞄准国际一流目标，在科研体制改革、年轻数学家成长、前沿课题研究等方面都取得令人高兴的突出成绩，为在新世纪把实验室建设成为国际一流的数学研究中心奠定了坚实基础。

　　实验室主任：丁伟岳教授，中国科学院院士，973专家顾问组成员，天元领导小组顾问。
　　实验室副主任：张平文教授、蒋美跃教授。
　　实验室学术委员会主任：姜伯驹教授，中国科学院院士，第三世界科学院院士，973首席科学家，天元领导小组顾问。

　　实验室现有全职研究人员45人，兼职研究人员3人，事务秘书1人。其中教授和博士导师37人，副教授8人，讲师3人，中科院院士6人，教育部长江特聘教授8人，杰出青年基金获得者14人，973首席科学家1人，973课题负责人5人，973课题组成员18人，跨世纪人才基金获得者5人，国家基金委重点项目主持人4人，课题组成员10人。实验室设学术秘书1人。

　　实验室设有4个子实验室：计算实验室，金融实验室，信息安全实验室，图像处理实验室；两个研究中心：几何分析中心，信息技术研究与开发中心。

　　实验室下设11个研究组，这些研究组以实验室的研究人员为主，由研究生、博士后并联合其它单位的数学家组成。这11个研究组是：几何分析，低维拓扑与微分几何，动力系统，代数与现代数论，现代分析，偏微分方程，概率论，统计学，计算数学，信息科学，应用数学。

　　实验室拥有一级学科博士授予权，含盖全部数学学科；拥有全部四个数学学科的国家重点学科。

 

北京大学“数学及其应用”教育部重点实验室是作为世界银行贷款“重点学科发展项目”于1989年建立的。1994年成为国家教委重点开放实验室，1995年通过了国家教委世界银行贷款项目专家组对实验室的验收检查；2000年被准予参加国家实验室评估，被评为国家A级重点实验室，名列当年数理口第三。2004年10月参加教育部重点实验室的评估，被评为优秀。2009年在教育部重点实验室的评估中，再次被评为优秀类实验室。

 

自实验室成立以来，在国家科技部、教育部和北京大学的领导和大力支持下，北京大学“数学及其应用”实验室根据世界数学发展潮流，瞄准国际一流目标，在科研体制改革、年轻数学家成长、前沿课题研究等方面都取得令人高兴的突出成绩，为在新世纪把实验室建设成为国际一流的数学研究中心奠定了坚实基础。

 

实验室现有全职研究人员53人，兼职研究人员3人，事务秘书1人。其中教授和博士导师40人，副教授10人，讲师3人，中科院院士6人，教育部长江特聘教授7人，杰出青年基金(A类)获得者16人，973首席科学家1人，973课题负责人5人，973课题组成员18人，跨世纪人才基金获得者5人，国家基金委重点项目主持人4人，课题组成员10人。实验室设学术秘书1人。

 

实验室设有4个子实验室：计算实验室，金融实验室，信息安全实验室，图像处理实验室；两个研究中心：几何分析中心，信息技术研究与开发中心。

 

实验室下设11个研究组：几何分析，低维拓扑与微分几何，动力系统，代数与组合数学，调和分析和偏微分方程，概率论，统计学，计算数学，信息科学，数学物理，金融数学。这些领域的研究都在蓬勃发展。

 

实验室拥有一级学科博士授予权，涵盖全部数学学科；拥有全部四个数学二级学科的国家重点学科。

 

现任实验室主任是张平文教授。实验室副主任是蒋美跃教授和甘少波教授。

  
现任实验室学术委员会主任为文兰教授，他是中国科学院院士，第三世界科学院院士，中国数学会第九届理事会理事长。学术委员会顾问为张恭庆院士、姜伯驹院士、丁伟岳院士和田刚院士。

 

 

 

 

http://math.nenu.edu.cn/index.html

东北师范大学应用统计实验室

　　 东北师范大学 应用统计教育部重点实验室(Key Laboratory for Applied Statistics of MOE，简记为KLAS)是按照“整合、优化、创新、发展”的基本原则，依托东北师范大学优势学科一概率论与数理统计，整合相关院所的五个实验室的优质资源组建而成。经过1年多的初期建设后，于2005年12月通过教育部组织的立项评审，继而于2006年6月通过教育部组织的建设计划论证。 　　实验室主要开展“用问题驱动的应用统计研究”，致力于 生物统计学，教育统计学，信息统计学和经济、金融统计学等领域的应用基础研究以及服务于国民经济建设和社会发展的大型数据处理技术方法研究。 　　实验室实行学术委员会指导下的实验室主任负责制。学术委员会由包括3名中科院院士在内的概率统计领域的著名专家15人组成，世界知名统计学家、美国伊利诺伊大学教授何旭铭教授出任学术委员会主任，著名数学家、中科院院士 马志明研究员出任名誉主任，校长 史宁中教授出任实验室主任。 　　实验室占地面积2329平方米，科研用房总建设面积3567平方米，仪器设备总额达1100多万元。经过多年的建设，实验室已成为具有一支在国际学术界有较强竞争力的学术梯队、具有较先进的大型计算现代化仪器设备和国内外有重要影响的高水平科学研究、人才培养的基地。 　　实验室现有固定人员总数27名，全部具有博士学位，其中第三世界科学院院士1人，教育部科学技术委员会理学部委员1人，国务院学科评议组成员1 人，吉林省特聘教授1人，国家级有突出贡献中青年专家1人，教授11名(全为博士生导师)。曾获国家杰出青年基金1项，入选教育部新世纪人才培养计划2 人。实验室还有流动人员总数50余名。

扩展阅读： http://klas.nenu.edu.cn

统计系于2004年成立，设有本科专业统计学。现有教师18人（均具有博士学位），其中教授8人（均为博士研究生导师）、副教授4人，第三世界科学院院士1人，国家级教学名师1人，国务院学位委员会学科评议组成员1人，国家杰出青年科学基金获得者1人。兼职教授3人：教育部“长江学者奖励计划”讲座教授：何旭铭教授（美国UIUC大学）；东师学者讲座教授：荆炳义（香港科技大学）；张华华教授（美国UIUC大学）。统计系下辖金融与信息工程研究中心和统计咨询中心。目前，统计系在读本科生150人，已毕业的本科生大部分已保送或考取研究生。本科生《概率论》、《数理统计》等专业基础课程采用英文原版教材授课，其中《数理统计》课程为2007年度国家精品课程。
    为了进一步扩大国际、国内合作交流，加强人才培养，自2006年以来，统计学专业举办或承办了多项重大、有影响的系列学术活动，如：“统计科学前沿问题——生物统计与生物信息学”国际学术研讨会（2006年）；全国博士生学术论坛——统计学及其应用（2007年）；东师现代统计讲习班（2008年）；全国研究生暑期学校（统计及其交叉科学）（2009年）。
    统计系主要有如下研究方向：应用概率、生物统计、教育心理统计、经济金融统计和信息统计等。研究内容涉及经济、金融、生物、医学、教育、心理、通讯和信息等多个跨学科交叉领域。统计系设有概率论与数理统计硕士点、博士点以及博士后科研流动站。本系在读硕士研究生80余人、博士研究生27人，科研流动站有博士后2人。本系教师在承担学院本科生和研究生教学任务的同时，还承担了大量科研任务。据统计，2005年以来本系教师在Annals of Statistics、Annals of Probability、J. Amer. Stat. Assoc.、J. Royal Statist. Society Ser. B、Biometrika、Biometrics等SCI检索的统计刊物上发表学术论文200余篇；自2008年以来在Springer出版社、World Scientific出版公司等出版英文专著3部，在科学出版社等出版中文专著5部。本系教师主持承担国家自然科学基金重点项目2项，国家自然科学基金面上项目、国家“973”计划子课题以及企事业单位委托的项目等十余项，累计科研经费一千余万元。近三年来所主持的科研项目、研究课题曾荣获教育部高等学校科学技术奖一、二等奖三项。
    统计系资料室藏书两万余册，中外文期刊400余种。本系有设备齐全的统计实验室，拥有微机90台，供师生教学与科研之用；拥有的“曙光机群”在高性能数据处理方面处于国内领先地位。

 

 

中国组合数学与图论学会http://www.cscgt.org/index.htm

理事长: 邵嘉裕（同济大学）         副理事长: 葛根年（浙江大学） 李学良 (南开大学) 王  军（上海师范大学）     秘书长: 殷剑兴（苏州大学）         副秘书长： 李雨生（同济大学）

常务理事（18名）：     常  安（福州大学） 常彦勋（北京交通大学） 陈永川（南开大学） 范更华（福州大学） 葛根年（浙江大学） 胡晓东（中国科学院） 康庆德（河北师范大学） 李学良（南开大学） 李雨生（同济大学） 刘桂真（山东大学） 孟吉翔（新疆大学） 邵嘉裕（同济大学） 孙智伟（南京大学） 王  军（上海师范大学） 王维凡（浙江师范大学） 许宝刚（南京师范大学） 殷剑兴（苏州大学） 张和平（兰州大学）

理事（33名）:     阿勇嘎（内蒙古师范大学） 陈北方（香港科技大学） 方新贵（北京大学） 冯荣权（北京大学 冯衍全（北京交通大学） 高维东（南开大学） 胡智全（华中师范大学） 黄元秋（湖南师范大学） 吉日木图（内蒙古民族大学） 季利均（苏州大学） 雷建国（河北师范大学） 李建平（云南大学） 李乔良（湖南师范大学） 陆  玫（清华大学） 苗正科（徐州师范大学） 钱建国（厦门大学） 沈  灏（上海交通大学） 束金龙（华东师范大学） 田子红（河北师范大学） 王  杰（国家基金委） 王  毅（大连理工大学） 吴佃华（广西师范大学） 吴建良（山东大学） 徐俊明（中国科技大学） 闫桂英（中国科学院） 晏卫根（集美大学） 臧文安（香港大学） 张胜贵（西北工业大学） 张胜元（福建师范大学） 张晓东（上海交通大学） 张之正（洛阳师范学院） 赵海兴（青海师范大学） 周  波（华南师范大学）

 

http://wenku.baidu.com/view/1e68f5cdda38376baf1fae0c.html

 

 

 

 

组合计数

　　 组合数学主要是研究某组离散对象满足一定条件的安排的存在性、构造及计数等问题。组合计数理论是组合数学中一个最基本的研究方向，主要研究 满足一定条件的安排方式的数目及其计数问题。本课程主要介绍组合数学中常见的和重要的一些 计数原理、计数方法和计数公式，包括一般的排列、组合的计算以及生成函数、容斥原理、反演原理、Polya 计数定理等等，是研究组合数学的初步。

 

组合数学之反演理论http://wenku.baidu.com/view/9e1a5829647d27284b735195.html

 

POLYA计数法http://www.docin.com/p-197371406.html

http://wenku.baidu.com/view/acc0e6c4aa00b52acfc7ca16.html

polya定理小结

　　polya定理是组合数学中比较难的一部分。首先需要对置换群、集合论有一定的了解，这样有助于理解burnside引理的证明。其次，polya定理只是对于在环上存在旋转、反射等等价的变换的一种计数方法，实际的题目中很多需要其他的知识来进行辅助。
　　环上的计数主要就是处理置换 -> 着色这种情况。很关键的一点是同一循环内着色相同。因此很多题目就在置换和着色上下文章。
　　最最简单的polya定理题目是置换数目很少，每种颜色不限，这种情况下只需手工数出所有的置换就可以了，一般就是一个公式。
　　难一点的要么是颜色数有限，需要用排列组合的知识或动态规划来帮助计数；要么是置换非常多，需要利用数论的知识来优化。当然还有其他的题型，比如对于相邻着色的限制，这样的题目就很困难了。

Redfield-Polya 定理是组合数学理论中最重要的定理之一．自从 1927 年 Redfield 首次运用 group reduction function 概念，现在称之为群的循环指标（circle index of a group），至今 60 多年来，他在许多实际计数问题上得到了广泛的应用，它以置换群为理论基础，与生成函数有机地结合在一起，揭示了一类具有组合意义的计数的规律性．

　　抽象地说在一集合内，定义了一个等价关系，人们往往关心由这个等价关系所决定的等价类的数目，Refield-Polya 理论就是为解决这类问题而发展起来的复杂计数理论．

　　为了帮助读者理解，本章例举了较多的实例．

§1 置换群的基本概念

　　设有限集合 ，集合中的元素称为“点”．集合 上的一个置换 是从 到自身上的 对应的映射：



设 是集合 上的另一个置换，置换 与 的乘积定义为复合映射：



　　例 1 设 上的二个置换：

和 ，

求乘积

　　解

从定义出发，



得：



　　设 是集合 上的全部置换构成的集合，在复合映射定一的乘义下，集合 构成一个群，称为 次对称群．对称群的任意子群称为置换群，因为它们都与集合 有关，一般也称为作用在 上的置换群．因为集合 的 排列有个，而每个排列对应一个置换，反之一个置换也对应一个排列，从而有

　　置换的另一种表示方法是循环表示，它可简化置换的表达方式．

　　设 是正整数，且满足，在置换 中就有一个循环



我们称它为置换 的一个 循环． 显然这里要求 个点互不相同，从而整数 是使 成立的最小正整数．由循环的定义，不难推出任意一个置换都可以表示成若干个互不相交的循环的积，即



　　例 2 将 化为互不相交循环积的形式．

　　解 先从点 计算， 故 有一个 3-循环 ，再从点 计算，，最后得： . 即 有 3-循环一个，2-循环一个，1-循环两个．有时为了简便，可将 1-循环省略不写，即：

　　由例 2 可看到 与 表示的置换是相同的．推广到一般情形，互不相交的循环积是可交换的，即：



这里 是 的互不相交的循环，

　　当两个循环的交非空时，两循环的乘积一般是不可交换的．

　　例如取例 1 中的 和 ，将它们分别化为不相交循环的乘积：

计算 ， ，比较可知

　　设置换 ，它的逆置换为：



这是因为 为恒等置换．

　　设置换 为互不相交的循环，则



　　对置换 ，使 成立的最小正整数 称为置换 的阶记为 ．由定义容易证明



其中 表示最小公倍数．

　　当 时，循环总可以写成若干个 循环和若干个 循环的乘积，此时若置换 中有偶数个循环， 称为偶置换；若有奇数个 2-循环， 称为奇置换．这个定义是有意义的，因为对任意的 循环 ，，有：若 是一个偶置换，那么 或 就一定是奇置换，由此可知，在对称群中，偶置换的数目与奇置换的数目相等，都等于 偶置换与奇置换的乘积仍为偶置换，在 中全部偶置换构成一个子群 ，称为次交错群，显然

　　设 与 是对称群 中的两个置换， 与 称之为共轭，如果存在使得

　　易知共轭关系为一个等价关系，从而中的置换划分为若干个共轭类，同一共轭类的所有置换在分解为互不相交循环的乘积下，具有相同的循环长度．这里的循环的长度是指一个循环中点的个数；反之具有相同的循环长度的两个置换一定共轭．即：在对称群中，两置换共轭的充分必要条件是它们具有相同的循环长度．

　　在对称群 中有多少个共轭类呢？先看一个简单的例子：

　　在对称群 中全部的共轭类为：

一个 循环，

一个 循环和一个 循环

二个 循环，

一个 循环，二个 循环，

四个 循环，

　　在 中一共有五个共轭类，而每一个共轭类恰好对应着数 4 的一种划分，即共轭类的数目等于整数4的划分数 ．

　　一般地，任意 次对称群 中的共轭类的数目等于正整数 的划分数 ．（ 的定义见第十一章）

　　在对称群 的每个共轭类中至少有多少个置换呢？我们知道循环长度决定一个共轭类，若此共轭类中的置换有 个 循环， 个 循环，， 个循环，这个共轭类记为 ， ， 这里 .若 ，则 被分解为 个互不相交的循环的乘积．

 

 

容斥原理
　　1．已知两个集合的大小，将这两个集合合并成一个集合，怎么求它的大小？
　　2．怎么求多个集合的并的大小？
　　3．在一个学校里，已知学至少k门课的学生的人次（k=1,2,…,n），求恰好学k门课的学生的人数（k=1,2,…,n）。
　　4．什么是反演？利用二项式反演及Mǒbíus反演能解决那些计数问题？
　　鸽巢原理
　　1．鸽巢原理有几种形式？
　　2．请给出鸽巢原理一两个简单的应用的例子。
　　3．请给出Ramsey定理的一个简单应用。
　　【学习目标】
　　容斥原理　
　　掌握由集合交的势求多个集合并的势及多个集合补的交的势的计数公式。并要掌握这些计数公式的推导方法并灵活运用这些公式解决实际问题。包括导出错排的计数和在有禁区的棋盘上布子的方案的计数。掌握二项式反演公式及其应用，掌握Mǒbíus函数和Mǒbíus反演，可重圆排列的计数。
　　鸽巢原理
　　鸽巢原理的几种形式，应用鸽巢原理的技巧，Ramsey问题，Ramsey数。
　　【学习指南】
　　容斥原理

|A∪B∪C| =|A|+|B|+|C|－|A∩B|－|A∩C|－|B∩C|＋|A∩B∩C|

　　先利用文氏图对两个，三个集合的并有直观的了解。然后推导n个公式的并的势的计数公式及几个集合的补的交的势的计数公式。在此基础上推出恰好属于k个集合的元素的个数。计算在有禁区的棋盘上布子的方案数，是运用容斥原理的一个典型例子。容斥原理可以说是一种迂回计数的方法，我们也可以从这个角度来看待反演。我们先从二项式着手，讨论错排问题，再讨论Mǒbíus反演，解决了可重圆排列问题。
　　鸽巢原理
　　从鸽巢原理的简单形式入手，掌握在实际例子中应用该原理的技巧。在掌握鸽巢原理的基础上通过简单例子入手逐步理解和掌握Ramsey定理。了解计算较小的Ramsey数的技巧。
　　【难重点】
　　容斥原理
　　容斥原理公式的证明（两种方法），夫妻围坐问题，一般公式的证明（两种方法），棋盘多项式，有禁区的布子问题，二项式反演，Mǒbíus反演，可重圆排列。
　　鸽巢原理
　　鸽巢原理的几种形式，鸽巢原理的应用技巧，Ramsey问题，Ramsey数。
　　【知识点】
　　容斥原理
　　容斥原理，一般公式，夫妻围坐问题（利用隔位组合），棋盘多项式，有禁区的布子问题，反演，二项式反演，Mǒbíus反演，可重圆排列。
　　鸽巢原理
　　鸽巢原理的简单形式，鸽巢原理的加强形式，鸽巢原理的应用技巧，Ramsey问题，Ramsey数。
http://comic.sjtu.edu.cn/thucs/GD_jsj_025y/text/chapter03/index/left.htm

 

 

 

组合优化

　　组合优化（Combinatorial Optimization）问题的目标是从组合问题的可行解集中求出最优解，通常可描述为：令Ω＝{s1，s2，…，sn}为所有状态构成的解空间，C(si)为状态si对应的目标函数值，要求寻找最优解s*，使得对于所有的si∈Ω，有C(s*)＝minC(si)。组合优化往往涉及排序、分类、筛选等问题，它是运筹学的一个重要分支。　　典型的组合优化问题有旅行商问题（Traveling Salesman Problem－TSP）、加工调度问题（Scheduling Problem，如Flow-Shop，Job-Shop）、0-1背包问题（Knapsack Problem）、装箱问题（Bin Packing Problem）、图着色问题（Graph Coloring Problem）、聚类问题（Clustering Problem）等。这些问题描述非常简单，并且有很强的工程代表性，但最优化求解很困难，其主要原因是求解这些问题的算法需要极长的运行时间与极大的存储空间，以致根本不可能在现有计算机上实现，即所谓的“组合爆炸”。正是这些问题的代表性和复杂性激起了人们对组合优化理论与算法的研究兴趣。

数学规划与组合优化
姚恩瑜, 何勇 ((数学)), 陈仕平
浙江大学出版社, 2001 - 247 页
本书是作者在多年开设的相关课程基础上编写而成的,系统地介绍了连续及离散优化的原理及方法。共分三篇,线性规划与整数线性规划、组合优化、非线性规划.
作 者： 姚恩瑜、何勇、陈仕平 主编 
出版社： 浙江大学出版社
ISBN： 730802816X 
价 格： 原价：25元 优惠价：21.3元　85折ISBN
出版时间： 2001-10第1版
在人类几乎所有的社会活动中都有“寻优”的需求，将寻优的过程用数学模型描述并求解，是20世纪应用数学的重大进展之一．数  学规划就是其中一类重要的数学模型．随着计算机科学的飞速发展，  针对离散变量的优化问题被逐渐重视，从而形成了有别于数学规划  的另一类重要模型，即组合优化（又称离散优化L作为两者之间的桥  梁则是线性规划和整数规划．线性规划是连续模型，它是数学规划的  基础问题，但由于它的解的特殊结构，它又能作为离散问题考虑．整。数规划是严格意义下的离散优化，但它的模型及求解均与连续的数  学规划密切相关．
      本书涉及的就是上述两类重要的优化模型，且在叙述中竭力避  免形成割裂的感觉，给读者以统一的寻优思想．作为教材，我们力求  讲清基本概念和基本求解方法的思想，所以在取材上着重经典方法  的介绍。
      本书是在作者多年教学的基础上编写而成的．上篇主要参考了  D．G．Luenberger Pf．著“ Introduction  to  linear  and  nonlinear  nro以ammins＼夏尊栓等译，科学出版社，1980年）中的有关部分改““写而成，下篇主要依照浙江大学讲义“非线性规划’丁韩继业、孙兰芬、  汤竞生、杨启帆、姚恩瑜编著）编写冲篇测是作者专门编写的．作者  对以上提及的各位致以衷心的感谢．
      本书上篇第一至第五章及第七章由陈仕平执笔，上篇第六章及  中篇各章由何勇执笔，下篇各章由姚恩瑜执笔．
      我们将连续与离散优化编写于一书之中，实为一种尝试，难免会  有很多不足之处，诚望得到读者的指正．
上篇 线性规划和整数线性规划
第一章 预备知识
§1．1凸集的定义及性质
§1．2超平面
§1．3 凸集的极点
习题
第二章 线性规划的基本性质
§2．1 线性规划问题的标准型
§2．2基本解和基本可行解
§2．3线性规划的基本定理
§2．4基本可行解与极点的关系
习题
第三章 单纯形法
§3．1 最优基本可行解的判断
§3．2基本可行解的改进
§3．3单纯形法概述
§3．4初始基本可行解的确定
§3．5 退化情况与bland法则
习题
第四章 对偶线性规划
§4．1 对偶线性规划的定义
§4．2 原问题与对偶问题解之间的关系
§4．3对偶单纯形法
§4．4灵敏度分析
习题
第五章 运输问题
§5．1 系数矩阵a的特征
§5．2 有关闭回路的一些基本概念
§5．3 求初始基本可行解的最小元素法
§5．4 最优解的判别方法——位势法
§5．5 基本可行解的改进
§5．6 产销不平衡的运输问题及其求解方法
§5．7应用举例
习题
第六章 线性规划的多项式时间算法
§6．1 线性规划与严格线性不等式组关系
§6．2仿射变换与椭球
§6．3 求解严格线性不等式组的椭球算法
§6．4求解karmarkar标准型的算法
§6．5 karmarkar算法的收敛性
§6．6化一般线性规划问题为karmarkar标准型
第七章 整数线性规划
§7．1整数线性规划问题及实例
§7．2分枝定界法
§7．3 gomory割平面法
§7．4 0—1规划
习题
中篇 组合优化
下篇 非线性规划

 

 

 

 

组合矩阵论（第二版）
作者： 柳柏濂   
丛书名： 研究生教学用书
出版社：科学出版社
ISBN：7030143663
上架时间：2006-2-14
出版日期：2006 年1月
本书介绍近20余年发展起来的一个新分支--组合矩阵论。内容包括矩阵和图的谱、矩阵的组合性质、非负矩阵的幂序列和矩阵方法与矩阵分析等。本书第一版是国内第一本介绍组合矩阵论的著作，填补了我国在这方面理论的空白。现在作为教育部审定的全国研究生教材重新出版，作者对原著作了增删，并补充了各章的习题和解答、必要的附录，更便于读者的教学和参考。.
　　本书适于作为信息科学、经济数学、计算机网络以及并行计算等方向的研究生教材，同时也是该方向科学工作者极好的参考用书。
第1章 矩阵和图的谱.
1.1 矩阵和图
1.2 谱的图论意义
1.3 图的特征值的估计
1.4 线图和全图的谱
1.5 同谱图
1.6 (0,1)矩阵的谱半径
习题1
参考文献
第2章 矩阵的组合性质
2.1 矩阵的置换相抵与置换相似
2.2 项秩与线秩
2.3 不可约方阵和完全不可分方阵
2.4 矩阵置换相似标准形和置换相抵标准形
2.5 几乎可约矩阵和几乎可分矩阵
2.6 积和式
2.7 具有一定行和、列和向量的(0,1)矩阵类
2.8 随机矩阵与双随机矩阵
2.9 birkhoff定理的拓广
习题2

.参考文献
第3章 非负矩阵的幂序列..
3.1 非负方阵与布尔方阵的幂序列
3.2 一次不定方程的frobenius问题
3.3 矩阵幂序列的振动周期
3.4 本原指数
3.5 一般幂敛指数
3.6 密度指数
3.7 本原指数的拓广——广义本原指数
3.8 完全不可分指数和hall指数
3.9 本原指数,直径和特征值
习题3
参考文献
第4章 矩阵方法与矩阵分析
4.1 常系数线性递归式求解的矩阵方法
4.2 图的二部分解
4.3 shannon容量
4.4 强正则图
4.5 矩阵和行列式的组合定义
4.6 (0,1)矩阵的最大行列式
4.7 (0,1)矩阵重排的极值问题
4.8 矩阵的完备消去概型
4.9 线性方程组的符号可解性
习题4
参考文献
习题提示或解答
附录
1.线性代数
2.图论
符号索引
名词索引...

感谢教育部和国务院学位委员会学科评议组的专家们，把此书推荐为全国研究生教学用书。.
　　此书出版后，一再重印。1998年被编人程民德院士主编的《现代数学基础丛书》中。2000年，正如徐利治教授在初版序言中所期望的，以本书为蓝本的英文版Matrices in Combinatorics and Graph Theory(Bolian Liu and Hong-jian Lai)在美国出版。近年来，我有幸参与了国家自然科学基金重点项目“组合矩阵论的研究”，感受到这一理论的蓬勃发展。因此借本书作为全国研究生用书再版之机，我有责任尽己所能再一次润饰，提炼和丰富它。我把全书的材料按当前研究的新进展作了补充，为了更适应教学的需要，把原书的论题作了精简，把第4、5章调整为一章，并增加了“4.9线性方程组的符号可解性”。各章配备了习题和解答，书末增加了关于线性代数和图论基础知识的附录。..
　　王元院士为本书第二版题写的书名和徐利治先生为原书所作的序言，对我是一个永远的鞭策和鼓励。感谢国家自然科学基金和广东省自然科学基金多年来对作者研究工作的支持。科学出版社从林鹏先生、刘嘉善先生到现在的杨波先生、姚莉丽女士一直关心和扶持本书的修订和出版，周波博士、尤利华博士协助做了文字的校正，借此向他们表示衷心的谢意。
　　学科的发展，不是一个人、一本书所能概括得了的。如果本书的出版，能够给读者在学习和探索组合矩阵论这门新兴学科中起到一点引示作用，这便是作者最大的心愿了。...
　　柳柏濂
　　2004.7于广州
　　
序言

最近我访问加拿大、美国等地归来，收到了柳柏濂教授寄来的新著《组合矩阵论》，连日展阅，觉得题材内容清新优美，喜不释手。.
　　特别可贵的是，这是一本成果丰硕的创造性著作，其中论述了中国中青年学者对组合矩阵论的一系列最新贡献，包括著者本人与李乔、邵嘉裕二位教授联合获得国家教委科技进步一等奖的合作成果。无疑，这些成果在国际上是居于领先地位的。
　　矩阵之能作为表现并分析组合论及图论问题的工具，这个很自然的思想，起源甚早，但“组合矩阵论”作为一个新的数学分支，开始被世界数学界所注目，实应归功于H.J.Ryser于1973年所做的演讲和著作。近年还出现了Brualdi和Ryser的专著。但柳柏濂的这本著作包含有不少新的题材内容，具有很不相同的特色。..
　　从这本新著可以看出，中国学者对发展“组合矩阵论”这一新分支居于特别重要的地位，而且还为今后的组合论研究工作者开辟出一些很有前途的新方向，故本人乐意为这本新著作序，并希望今后还将见到这本书的英译本能早日问世。...
　　徐利治
　　1994年2月16日
　　于大连理工大学数学科学研究所

 

 

 

 

排列组合

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。排列组合与古典概率论关系密切。

定义　　排列：从n个不同元素中，任取m（m≤n）个元素（被取出的元素各不相同），按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。

　　组合：从n个不同元素中，任取m（m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。

排列

　　公式P是排列公式，从N个元素取M个进行排列（即排序）。

（P是旧用法，现在教材上多用A，即Arrangement）

组合

　　公式C是组合公式，从N个元素取R个，不进行排列（即不排序）。

公式

　　1．排列及计算公式从n个不同元素中，任取m(m≤n)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 p(n,m)表示。 p(n,m)=n(n-1)(n-2)……(n-m+1)= n!/(n-m)!(规定0!=1)

　　. 2．组合及计算公式从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 c(n,m) 表示. c(n,m)=p(n,m)/m!=n!/((n-m)!*m!)；c(n,m)=c(n,n-m);

　　3．其他排列与组合公式从n个元素中取出r个元素的循环排列数=p(n,r)/r=n!/r(n-r)!. n个元素被分成k类，每类的个数分别是n1,n2,...nk这n个元素的全排列数为 n!/(n1!*n2!*...*nk!). k类元素，每类的个数无限,从中取出m个元素的组合数为c(m+k-1,m). 排列（Pnm(n为下标，m为上标)） Pnm=n×（n-1）。...（n-m+1）；Pnm=n！/（n-m）！（注：！是阶乘符号）；Pnn（两个n分别为上标和下标） =n！；0！=1；Pn1（n为下标1为上标）=n 组合（Cnm(n为下标，m为上标)） Cnm=Pnm/Pmm ；Cnm=n！/m！（n-m）！；Cnn（两个n分别为上标和下标） =1 ；Cn1（n为下标1为上标）=n；Cnm=Cnn-m

符号

　　

C-组合数

　　A-排列数 （在旧教材为P）

　　N-元素的总个数

　　R-参与选择的元素个数

!-阶乘，如5！=5×4×3×2×1=120

　　C-Combination 组合

　　P-Permutation排列 (现在教材为A-Arrangement)

　　一些组合恒等式

　　

排列组合常见公式

　　kCn/k=nCn-1/k-1(a/b,a在下，b在上)

　　Cn/rCr/m=Cn/mCn-m/r-m

历史

　　1772年，旺德蒙德以[n]p表示由n个不同的元素中每次取p个的排列数。而欧拉则于1771年以及于1778年以表示由n个不同元素中每次取出p个元素的组合数。至1872年，埃汀肖森引入了 以表相同之意，这组合符号（Signs of Combinations）一直 沿用至今。

　　1830年，皮科克引入符号Cr以表示由n个元素中每次取出 r个元素的组合数；1869年或稍早些，剑桥的古德文以符号nPr 表示由n个元素中每次取r个元素的排列数，这用法亦延用至今。按此法，nPn便相当於现在的n!。

　　1880年，鲍茨以nCr及nPr分别表示由n个元素取出r个的组合数与排列数；六年后，惠特渥斯以及表示相同之意，而且，他还以表示可重复的组合数。至1899年，克里斯托尔以nPr及nCr分别表示由n个不同元素中每次取出r个不重复之元素的排列数与组合数，并以nHr表示相同意义下之可重复的排列数，这三种符号也通用至今。

　　1904年，内托为一本百科辞典所写的辞条中，以表示上述nPr之意，以表示上述nCr之意，后者亦同时采用了。这些符号也一直用到现代。

组合数的奇偶

奇偶定义

　　对组合数C(n,k) (n>=k)：将n,k分别化为二进制，若某二进制位对应的n为0，而k为1 ，则C(n,k)为偶数；否则为奇数。

判定方法

　　组合数的奇偶性判定方法为：

　　结论：

　　对于C(n,k),若n&k == k 则c(n,k)为奇数，否则为偶数。

　　证明：

　　利用数学归纳法：

　　由C(n,k) = C(n-1,k) + C(n-1,k-1);

　　对应于杨辉三角：

　　1

　　1 1

　　1 2 1

　　1 3 3 1

　　1 4 6 4 1

　　………………

　　可以验证前面几层及k = 0时满足结论，下面证明在C(n-1,k)和C(n-1,k-1) (k > 0) 满足结论的情况下，

　　C(n,k)满足结论。

　　1).假设C(n-1,k)和C(n-1,k-1)为奇数：

　　则有：(n-1)&k == k;

　　(n-1)&(k-1) == k-1;

　　由于k和k-1的最后一位(在这里的位指的是二进制的位，下同)必然是不同的，所以n-1的最后一位必然是1

　　。

　　现假设n&k == k。

　　则同样因为n-1和n的最后一位不同推出k的最后一位是1。

　　因为n-1的最后一位是1，则n的最后一位是0，所以n&k != k，与假设矛盾。

　　所以得n&k != k。

　　2).假设C(n-1,k)和C(n-1,k-1)为偶数：

　　则有：(n-1)&k != k;

　　(n-1)&(k-1) != k-1;

　　现假设n&k == k.

　　则对于k最后一位为1的情况：

　　此时n最后一位也为1，所以有(n-1)&(k-1) == k-1，与假设矛盾。

　　而对于k最后一位为0的情况：

　　则k的末尾必有一部分形如：10; 代表任意个0。

　　相应的，n对应的部分为： 1{*}*; *代表0或1。

　　而若n对应的{*}*中只要有一个为1，则(n-1)&k == k成立，所以n对应部分也应该是10。

　　则相应的，k-1和n-1的末尾部分均为01,所以(n-1)&(k-1) == k-1 成立，与假设矛盾。

　　所以得n&k != k。

　　由1)和2)得出当C(n,k)是偶数时，n&k != k。

　　3).假设C(n-1,k)为奇数而C(n-1,k-1)为偶数：

　　则有：(n-1)&k == k;

　　(n-1)&(k-1) != k-1;

　　显然，k的最后一位只能是0，否则由(n-1)&k == k即可推出(n-1)&(k-1) == k-1。

　　所以k的末尾必有一部分形如：10;

　　相应的，n-1的对应部分为： 1{*}*;

　　相应的，k-1的对应部分为： 01;

　　则若要使得(n-1)&(k-1) != k-1 则要求n-1对应的{*}*中至少有一个是0.

　　所以n的对应部分也就为 ： 1{*}*; (不会因为进位变1为0)

　　所以 n&k = k。

　　4).假设C(n-1,k)为偶数而C(n-1,k-1)为奇数：

　　则有：(n-1)&k != k;

　　(n-1)&(k-1) == k-1;

　　分两种情况：

　　当k-1的最后一位为0时:

　　则k-1的末尾必有一部分形如： 10;

　　相应的，k的对应部分为 : 11;

　　相应的，n-1的对应部分为 : 1{*}0; (若为1{*}1,则(n-1)&k == k)

　　相应的，n的对应部分为 : 1{*}1;

　　所以n&k = k。

　　当k-1的最后一位为1时：

　　则k-1的末尾必有一部分形如: 01; (前面的0可以是附加上去的)

　　相应的，k的对应部分为 : 10;

　　相应的，n-1的对应部分为 : 01; (若为11，则(n-1)&k == k)

　　相应的，n的对应部分为 : 10;

　　所以n&k = k。

　　由3),4)得出当C(n,k)为奇数时，n&k = k。

　　综上，结论得证！

基本理论和公式

　　排列与元素的顺序有关，组合与顺序无关．如231与213是两个排列，2+3+1的和与2+1+3的和是一个组合．

(一)两个基本原理是排列和组合的基础

　　(1)加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+m3+…+mn种不同方法．

　　(2)乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法，……，做第n步有mn种不同的方法，那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法．

　　这里要注意区分两个原理，要做一件事，完成它若是有n类办法，是分类问题，第一类中的方法都是独立的，因此用加法原理；做一件事，需要分n个步骤，步与步之间是连续的，只有将分成的若干个互相联系的步骤，依次相继完成，这件事才算完成，因此用乘法原理．

　　这样完成一件事的分“类”和“步”是有本质区别的，因此也将两个原理区分开来．

(二)排列和排列数

　　(1)排列：从n个不同元素中，任取m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列．

　　从排列的意义可知，如果两个排列相同，不仅这两个排列的元素必须完全相同，而且排列的顺序必须完全相同，这就告诉了我们如何判断两个排列是否相同的方法．

　　(2)排列数公式：从n个不同元素中取出m(m≤n)个元素的所有排列

　　当m=n时，为全排列Pnn=n(n－1)(n－2)…3·2·1=n！

(三)组合和组合数

　　(1)组合：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从 n个不同元素中取出m个元素的一个组合．

　　从组合的定义知，如果两个组合中的元素完全相同，不管元素的顺序如何，都是相同的组合；只有当两个组合中的元素不完全相同时，才是不同的组合．

　　(2)组合数：从n个不同元素中取出m(m≤n)个元素的所有组合的个

　　这里要注意排列和组合的区别和联系，从n个不同元素中，任取m(m≤n)个元素，“按照一定的顺序排成一列”与“不管怎样的顺序并成一组”这是有本质区别的．

一、排列组合部分是中学数学中的难点之一

　　原因在于

　　(1)从千差万别的实际问题中抽象出几种特定的数学模型，需要较强的抽象思维能力；

　　(2)限制条件有时比较隐晦，需要我们对问题中的关键性词(特别是逻辑关联词和量词)准确理解；

　　(3)计算手段简单，与旧知识联系少，但选择正确合理的计算方案时需要的思维量较大；

　　(4)计算方案是否正确，往往不可用直观方法来检验，要求我们搞清概念、原理，并具有较强的分析能力。

二、两个基本计数原理及应用

　　(1)加法原理和分类计数法

　　1．加法原理

　　2．加法原理的集合形式

　　3．分类的要求

　　每一类中的每一种方法都可以独立地完成此任务；两类不同办法中的具体方法，互不相同(即分类不重)；完成此任务的任何一种方法，都属于某一类(即分类不漏)

　　(2)乘法原理和分步计数法

　　1．乘法原理

　　2．合理分步的要求

　　任何一步的一种方法都不能完成此任务，必须且只须连续完成这n步才能完成此任务；各步计数相互独立；只要有一步中所采取的方法不同，则对应的完成此事的方法也不同。

 

 

生成函数http://wenku.baidu.com/view/acd10892daef5ef7ba0d3c26.html

生成函数

生成函数即母函数，是组合数学中尤其是计数方面的一个重要理论和工具。最早提出母函数的人是法国数学家LaplaceP.S.在其1812年出版的《概率的分析理论》中明确提出。生成函数有普通型生成函数和指数型生成函数两种，其中普通型用的比较多。生成函数的应用简单来说在于研究未知（通项）数列规律，用这种方法在给出递推式的情况下求出数列的通项，生成函数是推导Fibonacci数列的通项公式方法之一。另外生成函数也广泛应用于编程与算法设计、分析上，运用这种数学方法往往对程序效率与速度有很大改进。

生成函数概述　　生成函数即母函数，是组合数学中尤其是计数方面的一个重要理论和工具。

　　生成函数有普通型生成函数和指数型生成函数两种，其中普通型用的比较多。形式上说，普通型生成函数用于解决多重集的组合问题，而指数型母函数用于解决多重集的排列问题。

　　最早提出母函数的人是法国数学家LaplaceP.S.在其1812年出版的《概率的分析理论》中明确提出“生成函数的计算”，书中对生成函数思想奠基人——Euler L在18世纪对自然数的分解与合成的研究做了延伸与发展。生成函数的理论由此基本建立。

　　生成函数的应用简单来说在于研究未知（通项）数列规律，用这种方法在给出递推式的情况下求出数列的通项，生成函数是推导Fibonacci数列的通项公式方法之一，另外组合数学中的Catalan数也可以通过生成函数的方法得到。

　　另外生成函数也广泛应用于编程与算法设计、分析上，运用这种数学方法往往对程序效率与速度有很大改进。

普通型母函数

　　定义：

　　对于任意数列a0,a1,a2...an 即用如下方法与一个函数联系起来：

　　~G(x) = a0 + a1x + a2x*2 + a3x^3 +....+ anx^n

　　则称G(x)是数列的生成函数(generating function)

　　例子：

　　比较典型的是：A(x) = (1+x)^n~C(n,0),C(n,1),C(n,2),C(n,3),.....,C(n,n)

　　基本运算：

　　<img src="file:///D:/Personal/Temp/moz-screenshot.jpg" alt=""> 用图片表示

指数型母函数

　　生成函数（也有叫做“母函数”的，但是我觉得母函数不太好听）是说，构造这么一个多项式函数g(x)，使得x的n次方系数为f(n)。

　　生成函数最绝妙的是，某些生成函数可以化简为一个很简单的函数。也就是说，不一定每个生成函数都是用一长串多项式来表示的。比如，这个函数f(n)=1 （n当然是属于自然数的），它的生成函数就应该是g(x)=1+x+x^2+x^3+x^4+...（每一项都是一，即使n=0时也有x^0系数为1，所以有常数项）。再仔细一看，这就是一个有无穷多项的等比数列求和嘛。如果-1<x<1，那么g(x)就等于1/(1-x)了。在研究生成函数时，我们都假设级数收敛，因为生成函数的x没有实际意义，我们可以任意取值。于是，我们就说，f(n)=1的生成函数是g(x)=1/(1-x)。

　　我们举一个例子说明，一些具有实际意义的组合问题也可以用像这样简单的一个函数全部表示出来。

　　考虑这个问题：从二班选n个MM出来有多少种选法。学过简单的排列与组合的同学都知道，答案就是C(4,n)。也就是说。从n=0开始，问题的答案分别是1,4,6,4,1,0,0,0,...（从4个MM中选出4个以上的人来方案数当然为0喽）。那么它的生成函数g(x)就应该是g(x)=1+4x+6x^2+4x^3+x^4。这不就是……二项式展开吗？于是，g(x)=(1+x)^4。

　　你或许应该知道，(1+x)^k=C(k,0)x^0+C(k,1)x^1+...+C(k,k)x^k；但你或许不知道，即使k为负数和小数的时候，也有类似的结论：(1+x)^k=C(k,0)x^0+C(k,1)x^1+...+C(k,k)x^k+C(k,k+1)x^(k+1)+C(k,k+2)x^(k+2)+...（一直加到无穷；式子看着很别扭，自己写到草稿纸上吧，毕竟这里输入数学式子很麻烦）。其中，广义的组合数C(k,i)就等于k(k-1)(k-2)(k-i+1)/i!，比如C(4,6)=4*3*2*1*0*(-1)/6!=0，再比如C(-1.4,2)=(-1.4)*(-2.4)/2!=1.68。后面这个就叫做牛顿二项式定理。当k为整数时，所有i>k时的C(k,i)中分子都要“越过”0这一项，因此后面C(k,k+1),C(k,k+2)之类的都为0了，与我们的经典二项式定理结论相同；不同的是，牛顿二项式定理中的指数k可以是任意实数。

　　我们再举一个例子说明一些更复杂的生成函数。n=x1+x2+x3+...+xk有多少个非负整数解？这道题是学排列与组合的经典例题了。把每组解的每个数都加1，就变成n+k=x1+x2+x3+...+xk的正整数解的个数了。教材上或许会出现这么一个难听的名字叫“隔板法”：把n+k个东西排成一排，在n+k-1个空格中插入k-1个“隔板”。答案我们总是知道的，就是C(n+k-1,k-1)。它就等于C(n+k-1,n)。它关于n的生成函数是g(x)=1/(1-x)^k。这个生成函数是怎么来的呢？其实，它就是(1-x)的-k次方。把(1-x)^(-k)按照刚才的牛顿二项式展开，我们就得到了x^n的系数恰好是C(n+k-1,n)，因为C(-k,n)*(-x)^n=[(-1)^n*C(n+k-1,n)]*[(-1)^n*x^n]=C(n+k-1,n)x^n。这里看晕了不要紧，后文有另一种方法可以推导出一模一样的公式。事实上，我们有一个纯组合数学的更简单的解释方法。因为我们刚才的几何级数1+x+x^2+x^3+x^4+...=1/(1-x)，那么(1+x+x^2+x^3+x^4+...)^k就等于1/(1-x)^k。仔细想想k个(1+x+x^2+x^3+x^4+...)相乘是什么意思。(1+x+x^2+x^3+x^4+...)^k的展开式中，n次项的系数就是我们的答案，因为它的这个系数是由原式完全展开后k个指数加起来恰好等于n的项合并起来得到的。

　　现在我们引用《组合数学》上暴经典的一个例题。很多书上都会有这类题。

　　我们要从苹果、香蕉、橘子和梨中拿一些水果出来，要求苹果只能拿偶数个，香蕉的个数要是5的倍数，橘子最多拿4个，梨要么不拿，要么只能拿一个。问按这样的要求拿n个水果的方案数。

　　结合刚才的k个(1+x+x^2+x^3+x^4+...)相乘，我们也可以算出这个问题的生成函数。

　　引用内容

　　g(x)=(1+x^2+x^4+...)(1+x^5+x^10+..)(1+x+x^2+x^3+x^4)(1+x)

　　=[1/(1-x^2)]*[1/(1-x^5)]*[(1-x^5)/(1-x)]*(1+x) （前两个分别是公比为2和5的几何级数，

　　第三个嘛，(1+x+x^2+x^3+x^4)*(1-x)不就是1-x^5了吗）

　　=1/(1-x)^2 （约分，把一大半都约掉了）

　　=(1-x)^(-2)=C(1,0)+C(2,1)x+C(3,2)x^2+C(4,3)x^3... （参见刚才对1/(1-x)^k的展开）

　　=1+2x+3x^2+4x^3+5x^4+....

　　于是，拿n个水果有n+1种方法。我们利用生成函数，完全使用代数手段得到了答案！

　　如果你对1/(1-x)^k的展开还不熟悉，我们这里再介绍一个更加简单和精妙的手段来解释1/(1-x)^2=1+2x+3x^2+4x^3+5x^4+....。

　　1/(1-x)=1+x+x^2+x^3+x^4+...是前面说过的。我们对这个式子等号两边同时求导数。于是，1/(1-x)^2=1+2x+3x^2+4x^3+5x^4+....。一步就得到了我们所需要的东西！不断地再求导数，我们同样可以得到刚才用复杂的牛顿二项式定理得到的那个结论（自己试试吧）。生成函数还有很多其它的处理手段，比如等式两边同时乘以、除以常数（相当于等式右边每一项乘以、除以常数），等式两边同时乘以、除以一个x（相当于等式右边的系数“移一位”），以及求微分积分等。神奇的生成函数啊。

　　我们用两种方法得到了这样一个公式：1/(1-x)^n=1+C(n,1)x^1+C(n+1,2)x^2+C(n+2,3)x^3+...+C(n+k-1,k)x^k+...。这个公式非常有用，是把一个生成函数还原为数列的武器。而且还是核武器。

　　接下来我们要演示如何使用生成函数求出Fibonacci数列的通项公式。

　　Fibonacci数列是这样一个递推数列：f(n)=f(n-1)+f(n-2)。现在我们需要求出它的生成函数g(x)。g(x)应该是一个这样的函数：

　　g(x)=x+x^2+2x^3+3x^4+5x^5+8x^6+13x^7+...

　　等式两边同时乘以x，我们得到：

　　x*g(x)=x^2+x^3+2x^4+3x^5+5x^6+8x^7+...

　　就像我们前面说过的一样，这相当于等式右边的所有系数向右移动了一位。

　　现在我们把前面的式子和后面的式子相加，我们得到：

　　g(x)+x*g(x)=x+2x^2+3x^3+5x^4+8x^5+...

　　把这最后一个式子和第一个式子好好对比一下。如果第一个式子的系数往左边移动一位，然后把多余的“1”去掉，就变成了最后一个式子了。由于递推函数的性质，我们神奇地得到了：g(x)+x*g(x)=g(x)/x-1。也就是说，g(x)*x^2+g(x)*x-g(x)=-x。把左边的g(x)提出来，我们有：g(x)(x^2+x-1)=-x。于是，我们得到了g(x)=x/(1-x-x^2)。

　　现在的任务是要把x/(1-x-x^2)还原成通项公式。这不是我们刚才的1/(1-x)^n的形式，我们要把它变成这种形式。我们发现，1-x-x^2=[1-(1-√5)x/2]*[1-(1+√5)x/2] （(1-√5)/2和(1+√5)/2是怎么算出来的？显然它们应该是x^2-x-1=0的两个根）。那么x/(1-x-x^2)一定能表示成?/[1-(1-√5)x/2]+?/[1-(1+√5)x/2]的形式（再次抱歉，输入数学公式很麻烦，将就看吧）。这是一定可以的，因为适当的?的取值可以让两个分式通分以后分子加起来恰好为一个x。?取值应该是多少呢？假设前面一个?是c1，后面那个是c2，那么通分以后分子为c1*[1-(1+√5)x/2]+c2*[1-(1-√5)x/2]，它恰好等于x。我们得到这样两个式子：常数项c1+c2=0，以及一次项-c1*(1+√5)/2-c2*(1-√5)/2=1。这两个式子足够我们解出c1和c2的准确值。你就不用解了，我用的Mathematica 5.0。解出来c1=-1/√5，c2=1/√5。你不信的话你去解吧。现在，我们把x/(1-x-x^2)变成了-(1/√5)/[1-(1-√5)x/2] + (1/√5)/[1-(1+√5)x/2]。我们已经知道了1/[1-(1-√5)x/2]的背后是以(1-√5)/2为公比的等比数列，1/[1-(1+√5)x/2]所表示的数列公比为(1+√5)/2。那么，各乘以一个常数，再相加，我们就得到了Fibonacci数列的通项公式：f(n)=-(1/√5)*[(1-√5)/2]^n + (1/√5)*[(1+√5)/2]^n。或许你会问，这么复杂的式子啊，还有根号，Fibonacci数列不都是整数吗？神奇的是，这个充满根号的式子对于任何一个自然数n得到的都是整数。熟悉用特征方程解线性递推方程的同学应该知道，以上过程实质上和找特征根求解没有区别。事实上，用上面所说的方法，我们可以求出任何一个线性齐次递推方程的通项公式。什么叫做线性齐次递推呢？就是这样的递推方程：f(n)等于多少个f(n-1)加上多少个f(n-2)加上多少个f(n-3)等等。Fibonacci数列的递推关系就是线性齐次递推关系。

　　我们最后看一个例子。我们介绍硬币兑换问题：我有1分、2分和5分面值的硬币。请问凑出n分钱有多少种方法。想一下刚才的水果，我们不难得到这个问题的生成函数：g(x)=(1+x+x^2+x^3+...)(1+x^2+x^4+...)(1+x^5+x^10+..)=1/[(1-x)(1-x^2)(1-x^5)]。现在，我们需要把它变成通项公式。我们的步骤同刚才的步骤完全相同。我们把(1-x)(1-x^2)(1-x^5)展开，得到1-x-x^2+x^3-x^5+x^6+x^7-x^8。我们求出-1+x+x^2-x^3+x^5-x^6-x^7+x^8=0的解，得到了以下8个解：-1,1,1,1,-(-1)^(1/5),(-1)^(2/5),-(-1)^(3/5),(-1)^(4/5)。这个不是我解出来的，我还是用的Mathematica 5.0。不是我不想解，而是我根本不会解这个8次方程。这也是为什么信息学会涉及这些东西的原因：次数稍微一高，只好交给计算机解决了。于是，(1-x)(1-x^2)(1-x^5)=(1+x)(1-x)^3(1+(-1)^(1/5) x)()()() （省略不写了）。注意那个(1-x)^3。由于等根的出现，我们不得不把(1-x)^3所包含的(1-x)和(1-x)^2因子写进一会儿的分母里，不然会导致解不出合适的c来。你可以看到很多虚数。不过没关系，这些虚数同样参与运算，就像刚才的根式一样不会影响到最后结果的有理性。然后，我们像刚才一样求出常数满足1/(1-x)(1-x^2)(1-x^5)=c1/()+c2/(1-x)+c3/(1-x)^2+c4/(1-x)^3...+c8/()。这个解太复杂了，我用Mathematica解了几分钟，打印出了起码几十KB的式子。虽然复杂，但我确实是得到了通项公式。你有兴趣的话可以尝试用Mathematica解决一下1/[(1-x)(1-x^3)] （只有1分和3分的硬币）。解c的值时可以用SolveAlways[]函数。你可以亲眼见到，一个四五行的充满虚数的式子最后总是得到正确的整数答案。 (我用的Mathematica7.0算了十几分钟怎么也算不完啊？4G的内存直接整出来个MemoryAllocationFailure）

　　生成函数还有很多东西，例如：Catalan数列啊，指数生成函数啊，之类的。我有空再说吧，已经5000多个字了。

　　huyichen一直在问那道题。很显然，那道题目和上面的兑换硬币有些联系。事实上，很多与它类似的题目都和生成函数有关。但那个题却没有什么可以利用生成函数的地方（或许我没想到吧）。或许每个max的值有什么方法用生成函数解出来，但整个题目是不大可能用生成函数解决的。

　　近来有个帖子问一道“DP天牛”题目的。那个题目也是这样，很多与它类似的题目都和DP有关，但那道题却不大可能动规。我总觉得它可以归约到装箱问题（考虑体积关系，最少要几个箱子才能把物品放完），而后者貌似属于NPC。或许我错了吧，现在没事就在研究理论的东西，很久没有想过OI题了，这方面的能力已经开始退化了。

　　Matrix67原创

扩展阅读：

• http://baike.baidu.com/view/1060108.html

• http://zhidao.baidu.com/question/45518164.html

• 《程序设计中的组合数学》吴文虎

• http://www.fish888.com/Catlan-Numbers-t149520

• （更简洁方法http://www.gzsx.net/Article/ShowArticle.asp?ArticleID=48）

• http://hiphotos.baidu.com/picofdice/mpic/item/0a8ce73c837a791fbba16776.jpg]（MathType制作）[图片http://hiphotos.baidu.com/picofdice/pic/item/21732b42e0641b0e9213c666.jpeg]：[图片http://hiphotos.baidu.com/picofdice/mpic/item/6044a1f8d0cac946242df228.jpg]

容斥原理

  

容斥原理

在计数时，必须注意无一重复，无一遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

详细推理

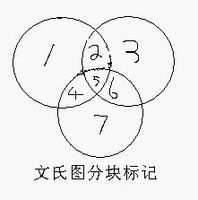
　　高等数学容斥原理公式 　　n(A1∪A2∪...∪Am)=∑n(Ai)1≤i≤m－∑n(Ai∩Aj)1≤i≤j≤m+∑n(Ai∩Aj∩Ak)－…+(-1)^m-1)n(A1∩A2…∩Am)1≤I,j,k≤m 　　两个集合的容斥关系公式：A∪B = A+B - A∩B (∩:重合的部分） 　　三个集合的容斥关系公式：A∪B∪C = A+B+C - A∩B - B∩C - C∩A +A∩B∩C 　　详细推理如下： 　　1、等式右边改造 = {【（A+B - A∩B）+C - B∩C】 - C∩A }+ A∩B∩C

  

 

2、文氏图分块标记如右图图：1245构成A，2356构成B，4567构成C 　　3、等式右边（）里指的是下图的1+2+3+4+5+6六部分： 　　那么A∪B∪C还缺部分7。　 　　4、等式右边【】号里+C（4+5+6+7）后，相当于A∪B∪C多加了4+5+6三部分， 　　减去B∩C（即5+6两部分）后，还多加了部分4。　 　　5、等式右边{}里减去C∩A （即4+5两部分）后，A∪B∪C又多减了部分5， 　　则加上A∩B∩C（即5）刚好是A∪B∪C。

容斥原理1

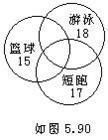
　　如果被计数的事物有A、B两类，那么，A类B类元素个数总和= 属于A类元素个数+ 属于B类元素个数—既是A类又是B类的元素个数。(A∪B = A+B - A∩B ) 　　例1　一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？

分析

　　依题意，被计数的事物有语、数得满分两类，“数学得满分”称为“A类元素”，“语文得满分”称为“B类元素”，“语、数都是满分”称为“既是A类又是B类的元素”，“至少有一门得满分的同学”称为“A类和B类元素个数”的总和。

答案

　　15+12-4=23

试一试

　　电视台向100人调查前一天收看电视的情况，有62人看过2频道，34人看过8频道，其中11人两个频道都看过。两个频道都没看过的有多少人？ 　　100-(62+34-11)=15

容斥原理2

　　如果被计数的事物有A、B、C三类，那么，A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。（A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C）

 

容斥原理

1．关键提示：

容斥原理关键内容就是两个公式，考生只要把这两个公式灵活掌握就可全面应对此类题型。另外在练习及真考的过程中，请借助图例将更有助于解题。

2．核心公式：

（1）两个集合的容斥关系公式：

  A＋B＝A∪B＋A∩B

（2）三个集合的容斥关系公式：

    A＋B＋C＝A∪B∪C＋A∩B＋B∩C＋C∩A－A∩B∩C

容斥原理
一、    知识要点
1、容斥原理
在计数时，常常遇到这样的情况，作合并运算时会把重复的部分多算，需要减去；作排除运算时会把重复部分多减，需要加上，这就是容斥原理。它的基本形式是：
  记A、B是两个集合，属于集合A的东西有 个，属于集合B的东西有 个，既属于集合A又属于集合B的东西记为 ，有 个；属于集合A或属于集合B的东西记为 ，有 个，则有： = + -
容斥原理可以用一个直观的图形来解释。如图，
左圆表示集合A，右圆表示集合B，两圆的公共部分表示 ，两圆合起来的部分表示 ，
由图可知： = + -
容斥原理又被称作包含排除原理或逐步淘汰原则。

 

 

 

分享

0

顶

阅读(145) ┊ 评论 (0) ┊ 收藏(0) ┊禁止转载 ┊ 顶 ▼ ┊ 打印 ┊ 举报

已投稿到：	排行榜

加载中，请稍候......

前一篇： IEEE—CS的计算机先驱奖(Computer Pioneer Award)

后一篇： 数学哲学(化) or 分析(化)哲学 ?