SVM（支持向量机）- 基本思想（一）

SVM（支持向量机）- 基本思想(一) 

Reference:

Pluskid系列博客

《Pattern recognition and machine learning》CM Bishop - 2006

          《convex optimization》SP Boyd, L Vandenberghe – 2004

       说明：本系列纯粹是pluskid博客的狗尾续貂之作，写下了只是想让自己踏踏实实学点东西，如果看懂了pluskid的博客，那就直接Pass,如果有不清楚的地方，说不定我的博客里面会给你一些启发。

1 Basic idear

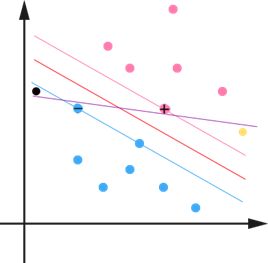
Figure 1

Question :

       假设样本为二维的情况，图中有红蓝两种点，代表已经有的两类样本数据，我们需要在红、蓝之间找一个分界面，使得分界面的一边是一类，另一边是另一类。很明显，会有很多个满足条件的平面，比如图中的紫色和深红色的两条直线，我们要找的是一个最优的超平面，使得对后续要分类的测试点，也能取得比较准确的分类，即泛化能力要强。例如，现在我们要对黑色和黄色两个测试点进行分类，我们仅有的信息就是蓝方和红方的分布，观察这两方的分布，直观上我们认为，黑色该属于蓝方，而棕色该属于红方。然而，紫色直线把黑色测试点分类为红方，黄色点分为蓝方，因此，相对深红色直线泛化能力略微逊色了点。那怎样的一条直线才是泛化能力最好的呢？这就是技术活了，直观上我们觉得紫色直线靠，两点太近了将紫色直线顺时针旋转一点点会效果更好，比如转到红色直线的位置。那红色直线具有什么样的属性呢？一般这种问题都会转化成为一个最优化问题，让数学来回答这个问题，SVM也不例外。

Answer :

       既然很多直线都能满足，那我们就找这里面最特殊的一条，特殊在于距离。在能正确区分训练集的直线集中，计算它门到最近样本点的距离，我们选择使得此距离最大的那条直线。

Formulation:

（1）点到直线的距离：

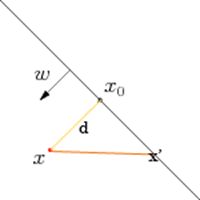
Figure 2

直线方程为 ，求点到该直线的距离

取直线上任意一点，则将向量往法向量投影得到

        

同时满足代入上式得

        

        

        但是求出来的距离在直线下方为负，在直线上方为正，而我们一般的类别标号就是取因此，就都统一为正的了。不过实际上每类样本取正还是负都没关系。假设为直线上方的样本点标号为时的解，现在将其变为负，即取为，要满足，显然此时的解。即法向量变换方向，也取反。直接决定了分界直线相对原点的偏移。易得原点到分界直线的距离。

（2）满足条件的直线中使得距离最近的点到直线的距离最大

        

是要找到样本点到特定直线的最近距离，是要找到使得最近距离最大的直线。

Opotimizing function

      优化(1.3)即得到我们要求的最优分界直线。但是直接优化(1.3)很困难，因为变化，对应的也可能会变化，使得优化过程中要在之间不断切换，弄得我们手忙脚乱。对于这种好动的函数，我们要像医生一样，给它绑起来（回忆下金刚狼的场景）。

注意到对任意，都可以通过对等比例缩放使得其为（固定），同时还能保证（等价）。那么优化(1.3)可简化成优化：

        

当然前提是我们能将最近的距离调节为1，于是加上约束条件（感觉像手铐脚链……）：

        

       优化之后总能使得两类样本都有点（向量）到分界线的函数距离：，如Figure 1中红色和蓝色穿直线穿过的点。正是在上的向量（即点）决定了分界线，因此它们被称为支持向量，而SVM是一个分类器，可以理解成能自动判别的机器，所以合称支持向量机。

       首先说明下为什么最终支持向量到分界线函数的距离是相等的，即 。试想下，如果一边距离远，一边距离近，考虑式(1.3)那么就对距离近的支持向量取，很明显，它的距离可以向距离远的这边移动来达到更大的值。因此，两类样本都不会让步，最终只能本着公平公正的原则取中间。

       为什么一定是呢？试想下，如果，很明显，将，那么也将缩小为1，那么式(1.4)将增大倍，因而不是最优值，因为就比它更优。因此，最终总能使得。

Further

       这里讨论的是二维的情况，对于三维的样本，可以拓展为分界平面，对于更高维的情况，可以拓展为分界超平面。

      对于线性不可分的情况，即无论如何都找不到一条直线能够完全区分出两类样本，即包容的点。允许它们犯点错误，使得。

      当错误已经大到忍无可忍的时候，我们将映射到高维空间，从而扩展成非线性分界曲线/面。

2 Optimizatin solving 待续