机器学习课程练习(三)——PCA与whitening
前言
斯坦福的UFLDL教程每一个章节都配有练习
本文是PCA与whitening这一章节的练习的解答
练习的目的是学习PCA与Whitening的基本知识
具体内容可以浏览课程网页
注意
这个练习的数据不是图像,要对每一维分别求均值,而不是对每个数据求自己的均值!
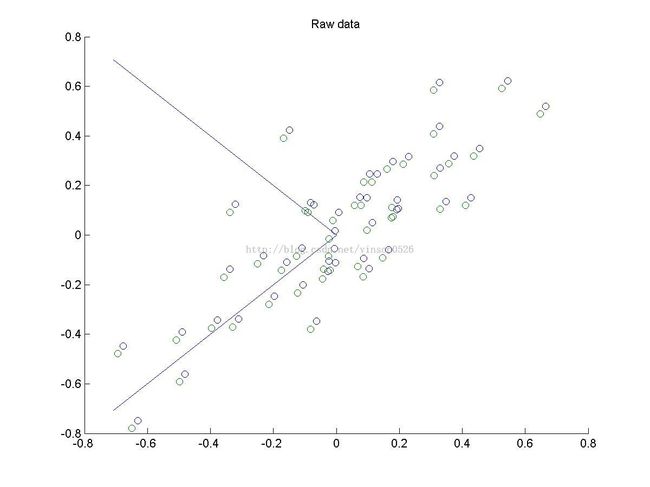
step 1a:获得PCA的U矩阵
u = zeros(size(x, 1)); % You need to compute this avg = mean(x,2); x= x - repmat(avg,1,size(x,2)); sigma = x * x' / size(x, 2); [u,s,v] = svd(sigma);
step 1b:计算x的旋转xRot
xRot = zeros(size(x)); % You need to compute this xRot = u' * x;
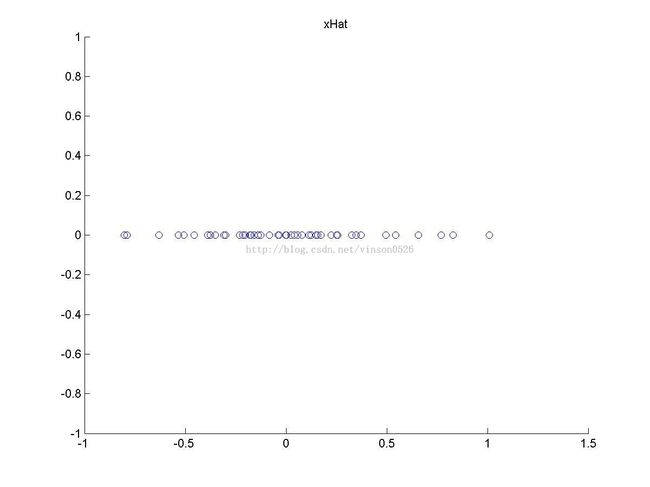
step 2:降维
xHat = zeros(size(x)); % You need to compute this xHat(1,:) = u(:,1)' * x;
step 3:PCA whitening
xPCAWhite = zeros(size(x)); % You need to compute this xPCAWhite = diag(1./sqrt(diag(s) + epsilon)) * u' * x;
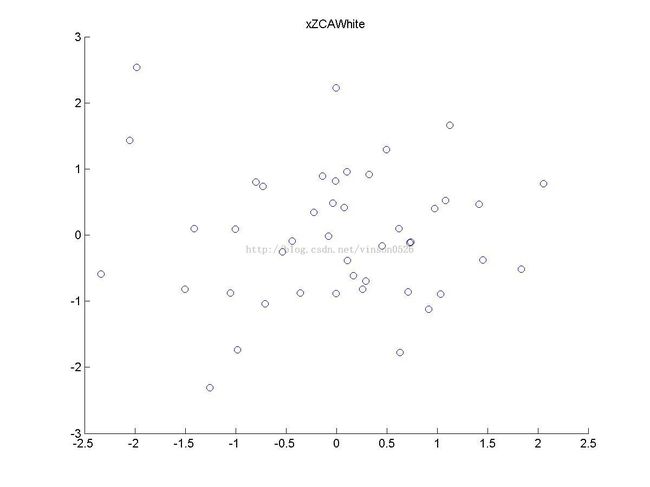
step 4:ZCA whitening
xZCAWhite = zeros(size(x)); % You need to compute this xZCAWhite = u * xPCAWhite;
完整代码:
close all
%%================================================================
%% Step 0: Load data
% We have provided the code to load data from pcaData.txt into x.
% x is a 2 * 45 matrix, where the kth column x(:,k) corresponds to
% the kth data point.Here we provide the code to load natural image data into x.
% You do not need to change the code below.
x = load('pcaData.txt','-ascii');
figure(1);
scatter(x(1, :), x(2, :));
title('Raw data');
%%================================================================
%% Step 1a: Implement PCA to obtain U
% Implement PCA to obtain the rotation matrix U, which is the eigenbasis
% sigma.
% -------------------- YOUR CODE HERE --------------------
u = zeros(size(x, 1)); % You need to compute this
avg = mean(x,2);
x= x - repmat(avg,1,size(x,2));
sigma = x * x' / size(x, 2);
[u,s,v] = svd(sigma);
% --------------------------------------------------------
hold on
plot([0 u(1,1)], [0 u(2,1)],'-');
plot([0 u(1,2)], [0 u(2,2)],'-');
scatter(x(1, :), x(2, :));
hold off
%%================================================================
%% Step 1b: Compute xRot, the projection on to the eigenbasis
% Now, compute xRot by projecting the data on to the basis defined
% by U. Visualize the points by performing a scatter plot.
% -------------------- YOUR CODE HERE --------------------
xRot = zeros(size(x)); % You need to compute this
xRot = u' * x;
% --------------------------------------------------------
% Visualise the covariance matrix. You should see a line across the
% diagonal against a blue background.
figure(2);
scatter(xRot(1, :), xRot(2, :));
title('xRot');
%%================================================================
%% Step 2: Reduce the number of dimensions from 2 to 1.
% Compute xRot again (this time projecting to 1 dimension).
% Then, compute xHat by projecting the xRot back onto the original axes
% to see the effect of dimension reduction
% -------------------- YOUR CODE HERE --------------------
k = 1; % Use k = 1 and project the data onto the first eigenbasis
xHat = zeros(size(x)); % You need to compute this
xHat(1,:) = u(:,1)' * x;
% --------------------------------------------------------
figure(3);
scatter(xHat(1, :), xHat(2, :));
title('xHat');
%%================================================================
%% Step 3: PCA Whitening
% Complute xPCAWhite and plot the results.
epsilon = 1e-5;
% -------------------- YOUR CODE HERE --------------------
xPCAWhite = zeros(size(x)); % You need to compute this
xPCAWhite = diag(1./sqrt(diag(s) + epsilon)) * u' * x;
% --------------------------------------------------------
figure(4);
scatter(xPCAWhite(1, :), xPCAWhite(2, :));
title('xPCAWhite');
%%================================================================
%% Step 3: ZCA Whitening
% Complute xZCAWhite and plot the results.
% -------------------- YOUR CODE HERE --------------------
xZCAWhite = zeros(size(x)); % You need to compute this
xZCAWhite = u * xPCAWhite;
% --------------------------------------------------------
figure(5);
scatter(xZCAWhite(1, :), xZCAWhite(2, :));
title('xZCAWhite');
%% Congratulations! When you have reached this point, you are done!
% You can now move onto the next PCA exercise. :)