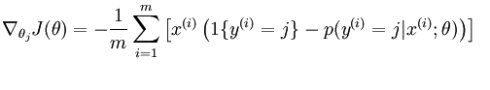Machine Learning系列实验--SoftMax Regression

原文地址：http://blog.sina.com.cn/s/blog_6982136301015asd.html

SoftMax回归可以用来进行两种以上的分类，很是神奇！实现过程实在有点坎坷，主要是开始写代码的时候理解并不透彻，而且思路不清晰，引以为戒吧！

SoftMax Regression属于指数家族，证明见（ http://cs229.stanford.edu/notes/cs229-notes1.pdf  及 http://ufldl.stanford.edu/wiki/index.php/Softmax_Regression），最后得出的结论是：

最后写出似然估计： 




之后采用梯度或牛顿方法进行逼近：

注意，上面公式采用的是批量梯度，随机梯度当然也是可以的。

参数theta的更新如下：

要注意的是，theta[j]是一个向量。

实验还是参考大牛pennyliang（ http://blog.csdn.net/pennyliang/article/details/7048291），代码如下：

1. #include <iostream>  
2. #include <cmath>  
3. #include <assert.h>  
4. using namespace std;  
5.   
6. const int K = 2;//有K+1类  
7. const int M = 9;//训练集大小  
8. const int N = 4;//特征数  
9.   
10. double x[M][N]={{1,47,76,24}, //include x0=1  
11.     {1,46,77,23},  
12.     {1,48,74,22},  
13.     {1,34,76,21},  
14.     {1,35,75,24},  
15.     {1,34,77,25},  
16.     {1,55,76,21},  
17.     {1,56,74,22},  
18.     {1,55,72,22},  
19. };  
20.   
21. double y[M]={1,  
22.     1,  
23.     1,  
24.     2,  
25.     2,  
26.     2,  
27.     3,  
28.     3,  
29.     3,};  
30.   
31. double theta[K][N]={  
32.     {0.3,0.3,0.01,0.01},  
33.     {0.5,0.5,0.01,0.01}}; // include theta0  
34.   
35. double h_value[K];//h(x)向量值  
36.   
37. //求exp（QT*x）  
38. double fun_eqx(double* x, double* q)  
39. {  
40.     double sum = 0;  
41.     for (int i = 0; i < N; i++)  
42.     {  
43.         sum += x[i] * q[i];  
44.     }  
45.     return pow(2.718281828, sum);  
46. }  
47.   
48. //求h向量  
49. void h(double* x)  
50. {  
51.     int i;  
52.     double sum = 1;//之前假定theta[K+1]={0},所以exp(Q[K+1]T*x)=1  
53.     for (i = 0; i < K; i++)  
54.     {  
55.         h_value[i] = fun_eqx(x, theta[i]);  
56.         sum += h_value[i];  
57.     }  
58.       
59.     assert(sum != 0);  
60.       
61.     for (i = 0; i < K; i++)  
62.     {  
63.         h_value[i] /= sum;   
64.     }  
65. }  
66.   
67. void modify_stochostic()  
68. {  
69.     //随机梯度下降，训练参数  
70.     int i, j, k;  
71.     for (j = 0; j < M; j ++)  
72.     {  
73.         h(x[j]);  
74.         for (i = 0; i < K; i++)  
75.         {  
76.             for (k = 0; k < N; k++)  
77.             {  
78.                 theta[i][k] += 0.001 * x[j][k] *  ((y[j] == i+1?1:0) - h_value[i]);  
79.             }  
80.         }  
81.     }  
82. }  
83. void modify_batch()  
84. {  
85.     //批量梯度下降，训练参数  
86.     int i, j, k ;  
87.     for (i = 0; i < K; i++)  
88.     {  
89.         double sum[N] = {0.0};  
90.         for (j = 0; j < M; j++)  
91.         {  
92.             h(x[j]);  
93.             for (k = 0; k < N; k++)  
94.             {  
95.                 sum[k] += x[j][k] * ((y[j] == i+1?1:0) - h_value[i]);  
96.             }  
97.         }  
98.         for (k = 0; k < N; k++)  
99.         {  
100.             theta[i][k] += 0.001 * sum[k] / N;  
101.         }  
102.     }  
103. }  
104.   
105. void train(void)  
106. {  
107.     int i;  
108.     for (i = 0; i < 10000; i++)  
109.     {  
110.         //modify_stochostic();  
111.         modify_batch();  
112.     }  
113. }  
114.   
115. void predict(double* pre)  
116. {  
117.     //输出预测向量  
118.     int i;  
119.     for (i = 0; i < K; i++)  
120.         h_value[i] = 0;  
121.     train();  
122.     h(pre);  
123.     for (i = 0; i < K; i++)  
124.         cout << h_value[i] << " ";  
125.     cout << 1 - h_value[0] - h_value[1] << endl;  
126. }  
127.   
128. int main(void)  
129. {  
130.     for (int i=0; i < M; i++)  
131.     {  
132.         predict(x[i]);  
133.     }  
134.     cout << endl;  
135.     double pre[] = {1,20, 80, 50 };  
136.     predict(pre);  
137.     return 0;  
138. }  

代码实现了批量梯度和随机梯度两种方法，实验最后分别将训练样本带入进行估计，迭代10000次的结果为：

stochastic:

0.999504 0.000350044 0.000145502

0.997555 0.00242731 1.72341e-005

0.994635 1.24138e-005 0.00535281

2.59353e-005 0.999974 6.07695e-017

0.00105664 0.998943 -1.09071e-016

4.98481e-005 0.99995 3.45318e-017

0.0018048 1.56509e-012 0.998195

0.000176388 1.90889e-015 0.999824

0.000169041 8.42073e-016 0.999831

batch:

0.993387 0.00371185 0.00290158

0.991547 0.0081696 0.000283336

0.979246 0.000132495 0.0206216

0.000630111 0.99937 4.9303e-014

0.00378715 0.996213 9.37462e-014

0.000299602 0.9997 3.50739e-017

0.00759726 2.60939e-010 0.992403

0.0006897 1.09856e-012 0.99931

0.000545117 5.19157e-013 0.999455

可见随机梯度收敛的更快。

对于预测来说，输出结果每行的三个数表示是：对于输入来说，是1 2 3三类的概率分别是多少。