HUD1728:逃离迷宫
逃离迷宫Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 9379 Accepted Submission(s): 2209
Problem Description
给定一个m × n (m行, n列)的迷宫,迷宫中有两个位置,gloria想从迷宫的一个位置走到另外一个位置,当然迷宫中有些地方是空地,gloria可以穿越,有些地方是障碍,她必须绕行,从迷宫的一个位置,只能走到与它相邻的4个位置中,当然在行走过程中,gloria不能走到迷宫外面去。令人头痛的是,gloria是个没什么方向感的人,因此,她在行走过程中,不能转太多弯了,否则她会晕倒的。我们假定给定的两个位置都是空地,初始时,gloria所面向的方向未定,她可以选择4个方向的任何一个出发,而不算成一次转弯。gloria能从一个位置走到另外一个位置吗?
Input
第1行为一个整数t (1 ≤ t ≤ 100),表示测试数据的个数,接下来为t组测试数据,每组测试数据中,
第1行为两个整数m, n (1 ≤ m, n ≤ 100),分别表示迷宫的行数和列数,接下来m行,每行包括n个字符,其中字符'.'表示该位置为空地,字符'*'表示该位置为障碍,输入数据中只有这两种字符,每组测试数据的最后一行为5个整数k, x 1, y 1, x 2, y 2 (1 ≤ k ≤ 10, 1 ≤ x 1, x 2 ≤ n, 1 ≤ y 1, y 2 ≤ m),其中k表示gloria最多能转的弯数,(x 1, y 1), (x 2, y 2)表示两个位置,其中x 1,x 2对应列,y 1, y 2对应行。
Output
每组测试数据对应为一行,若gloria能从一个位置走到另外一个位置,输出“yes”,否则输出“no”。
Sample Input
Sample Output
Source
“网新恩普杯”杭州电子科技大学程序设计邀请赛
Recommend
lcy
|
=====================================算法分析=====================================
BFS:BFS算法是一种扩展式的搜索算法,这个“扩展”的对象可以有多种。
理解了这个题目中扩展的对象以及扩展的方法,代码也就很容易写出来了。
比如HDU1372:Knight Moves中,求解棋盘上“马”从一个坐标走到另一个坐标所需的最少步数,扩展的对象就是步数——由走K步
能到达的点扩展出走K+1步能到达的点。
那么类似得,对于这个题目,只需要把扩展的对象理解为转弯次数即可——由转弯K次能到达的点扩展出转弯K+1次能到达的点。
至于如何扩展,这也很容易想到:由一个点,走向它上下左右四个方向上“所有未被访问过”的点,转弯次数+1。但由于题目
的特别说明,起点要排除在外。
=====================================数据处理=====================================
1、注意起点和终点坐标的输入是先输入列后输入行的。
2、前面已经提到,对起点的扩展需要特殊处理。为了方便,下面的代码没有进行特殊处理而是把最大转弯次数+1,答案依然正确。
3、输入的起点和终点坐标是从1开始编号的,而数组是从0开始编号的,因此需要把输入的起点和终点的横纵坐标值减1。
=======================================代码=======================================
#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
#define FRQ(CUR) Frq[CUR.y][CUR.x] //坐标CUR对应的Frq
#define MAP(CUR) Map[CUR.y][CUR.x] //坐标CUR对应的Map
#define SAME(A,B) (A.x==B.x)&&(A.y==B.y) //坐标A与B是否相同
#define LEGCORD(CUR) (0<=CUR.x&&CUR.x<N&&0<=CUR.y&&CUR.y<M) //坐标CUR是否合法
const int Dir[4][2]={{0,-1},{0,1},{-1,0},{1,0}};
int C,M,N,K,Frq[105][105];
char Map[105][105];
struct coord { int x,y; }S,E;
void BFS()
{
if(SAME(S,E)) { puts("yes"); return; }
memset(Frq,-1,sizeof(Frq));
FRQ(S)=0;
queue<coord>q;
for(q.push(S);!q.empty();q.pop())
{
struct coord cur=q.front();
for(int n=0;n<4;++n)
{
struct coord tmp=cur;
while(1)
{
tmp.x+=Dir[n][0];
tmp.y+=Dir[n][1];
if(!(LEGCORD(tmp)&&MAP(tmp)=='.'&&FRQ(tmp)==-1)) break; //扩展点now在dir方向上所有合法的未被访问过的点
FRQ(tmp)=FRQ(cur)+1;
if(FRQ(tmp)>K) { puts("no"); return; }
if(SAME(tmp,E)) { puts("yes"); return; }
q.push(tmp);
}
}
}
puts("no");
}
void ReaData()
{
scanf("%d%d",&M,&N);
for(int i=0;i<M;++i)
{
scanf("%*c%s",Map[i]);
}
scanf("%d%d%d%d%d",&K,&S.x,&S.y,&E.x,&E.y);
++K; --S.x; --S.y; --E.x; --E.y; //数据处理部分已说明
}
int main()
{
while(scanf("%d",&C)==1) while(C--)
{
ReaData();
BFS();
}
return 0;
}
=======================================修正=======================================
这份看起来完全正确的代码却会被OJ判以WA。。。与标程对拍了6000组左右的随机数据后,总算得到了一组使以上代码答案错误的数
据,裁剪后如下:
3 2
..
..
*.
1 1 1 2 3
对于这组数据,很容易看出正确答案应当是“yes”,但程序给出的答案却是“no” 。稍微想想,算法思想是肯定没问题的,那就是
代码实现出错了。
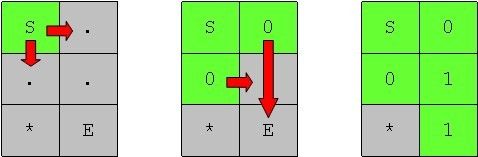
这是根据算法对该数据的搜索过程示意图:从起点S到终点E的转弯次数为1。

不难发现:出错原因是点(2,1)向下扩展时,已经访问过的点(2,2)阻止了它的扩展导致其扩展不完全。
观察代码:向某个方向持续扩展判断条件之一的 FRQ(tmp) == -1 本是为了避免重复访问,但在上述的案例中却引发了错误。
解决方法:去除这个判断条件,使得已访问过的点不阻止点的扩展,但对于已访问过的点不做处理即可。
while(1)
{
tmp.x+=Dir[n][0];
tmp.y+=Dir[n][1];
if(!(LEGCORD(tmp)&&MAP(tmp)=='.')) break; //扩展点now在dir方向上所有合法的未被访问过的点
if(FRQ(tmp)!=-1) continue; //对于已访问过的点不做处理
FRQ(tmp)=FRQ(cur)+1;
if(FRQ(tmp)>K) { puts("no"); return; }
if(SAME(tmp,E)) { puts("yes"); return; }
q.push(tmp);
}
=======================================优化=======================================
设点Cur向某个方向扩展时遇上了一个已经被访问过了的点V,下面分类讨论从起点到点Cur的转弯次数FRQ(Cur)与从起点到点V的转弯
次数FRQ(V)的大小关系:
1、FRQ(Cur)>FRQ(V),那么点V肯定在点Cur之前就已经该方向上进行了扩展,因此这个方向上不存在未被访问过的点,点Cur放弃扩
展不会出错。
2、FRQ(Cur)=FRQ(V),即使该方向上V点之后的那些未被访问过的点通过V扩展得到,也不会出错,因为被赋值为FRQ(Cur)+1与被赋值
为FRQ(V)+1是一样的。
3、FRQ(Cur)<FRQ(V),此时若该方向上V点之后的那些未被访问过的点通过V扩展得到,其转弯次数FRQ(V)+1将会大于FRQ(Cur)+1而出
错!就像上面那组数据一样。
综上所诉:当点Cur向某个方向扩展时遇上了一个已经被访问过了的点V时,在FRQ(Cur)<FRQ(V)才需要往该方向继续扩展。
由此可知:只需把原代码中的FRQ(tmp)==-1改为FRQ(tmp)==-1||FRQ(tmp)>FRQ(now),同时对于已访问过的点仍然不做处理即可。优化
后运行数据及其修正部分如下:
![]()
while(1)
{
tmp.x+=Dir[n][0];
tmp.y+=Dir[n][1];
if(!(LEGCORD(tmp)&&MAP(tmp)=='.')&&(FRQ(tmp)==-1||FRQ(tmp)>FRQ(cur))) break;
if(FRQ(tmp)!=-1) continue; //对于已访问过的点不做处理
FRQ(tmp)=FRQ(cur)+1;
if(FRQ(tmp)>K) { puts("no"); return; }
if(SAME(tmp,E)) { puts("yes"); return; }
q.push(tmp);
}