poj3131Cubic Eight-Puzzle(立体8数码,双向bfs+6进制压缩)
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 1301 | Accepted: 434 |
Description
Let’s play a puzzle using eight cubes placed on a 3 × 3 board leaving one empty square.
Faces of cubes are painted with three colors. As a puzzle step, you can roll one of the cubes to a adjacent empty square. Your goal is to make the specified color pattern visible from above by a number of such steps.
The rules of this puzzle are as follows.
-
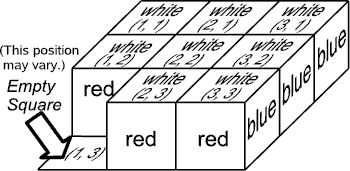
Coloring of Cubes: All the cubes area colored in the same way as shown in Figure 1. The opposite faces have the same color.
Figure 1: Coloring of a cube
-
Initial Board State: Eight cubes are placed on the 3 × 3 board leaving one empty square. All the cubes have the same orientation as shown in Figure 2. As shown in the figure, squares on the board are given x andy coordinates, (1, 1), (1, 2), …, and (3, 3). The position of the initially empty square may vary.
Figure 2: Initial board state
-
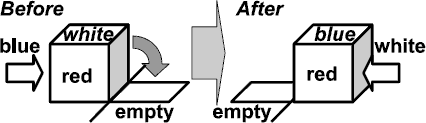
Rolling Cubes: At each step, we can choose one of the cubes adjacent to the empty square and roll it into the empty square, leaving the original position empty. Figure 3 shows an example.
Figure 3: Rolling a cube
-
Goal: The goal of this puzzle is to arrange the cubes so that their top faces form the specified color pattern by a number of cube rolling steps described above.
Your task is to write a program that finds the minimum number of steps required to make the specified color pattern from the given initial state.
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets is less than 16. Each dataset is formatted as follows.
x y F11 F21 F31 F12 F22 F32 F13 F23 F33
The first line contains two integers x and y separated by a space, indicating the position (x, y) of the initially empty square. The values of x and y are 1, 2, or 3.
The following three lines specify the color pattern to make. Each line contains three characters F1j, F2j, and F3j, separated by a space. Character Fij indicates the top color of the cube, if any, at the position (i, j) as follows:
B:Blue,
W:White,
R:Red,
E:the square is Empty.
There is exactly one ‘E’ character in each dataset.
Output
For each dataset, output the minimum number of steps to achieve the goal, when the goal can be reached within 30 steps. Otherwise, output “-1” for the dataset.
Sample Input
1 2 W W W E W W W W W 2 1 R B W R W W E W W 3 3 W B W B R E R B R 3 3 B W R B W R B E R 2 1 B B B B R B B R E 1 1 R R R W W W R R E 2 1 R R R B W B R R E 3 2 R R R W E W R R R 0 0
Sample Output
0 3 13 23 29 30 -1 -1
Source
#include <iostream>
#include<cstdio>
#include<cstring>
#include<cctype>
using namespace std;
const int d1 = 21;
const int d2 = 9;
const int M = 100005;
const int N = 1679616;//6^8
bool flag[2][N][9];//3690kb
int fac[] = {1,6,36,216,1296,7776,46656,279936};
//6个状态:
//状态号 上 前 右
//0 W R B
//1 W B R
//2 R W B
//3 R B W
//4 B W R
//5 B R W
int roll[6][2] = {{2,5},{4,3},{0,4},{5,1},{1,2},{3,0}};
//6个状态分别往上下左右4个方向转一步到达的新状态
struct node
{
int state;
short int pos,step;
}ss,now;
struct que
{
struct node t[M];
int head,tail;
void init()
{
head = tail;
}
bool empty()
{
return head == tail;
}
struct node top()
{
return t[head];
}
void pop()
{
head ++;
if(head == M)
head = 0;
}
void push(struct node a)
{
t[tail] = a;
tail ++;
if(tail == M)
tail = 0;
if(tail + 1 == head)
printf("queue full\n");
}
}q[2];
int x,y;
int endstate[10];
int endpos;
void dfs(int cur,int sum,int dp)
{
if(cur == -1)
{
ss.state = sum;
ss.pos = endpos;
ss.step = 0;
q[1].push(ss);
flag[1][ss.state][ss.pos] = 1;
return;
}
if(endstate[cur] == -1)
dfs(cur - 1,sum,dp);
else
{
int i;
for(i = endstate[cur];i <= endstate[cur] + 1;i ++)
dfs(cur - 1,sum + i * fac[dp],dp + 1);
}
}
int getdigit(int a,int b)//从6进制数a中得到低位第b+1位
{
int ret;
a /= fac[b];
ret = a % 6;
return ret;
}
int main()
{
int i,j,k;
char s[3];
while(scanf("%d%d",&y,&x),(x + y))
{
for(i = 0;i < 3;i ++)
{
for(j = 0;j < 3;j ++)
{
scanf("%s",s);
switch(*s)
{
case 'W':endstate[i * 3 + j] = 0;break;
case 'R':endstate[i * 3 + j] = 2;break;
case 'B':endstate[i * 3 + j] = 4;break;
case 'E':endstate[i * 3 + j] = -1;
endpos = i * 3 + j;break;
}
}
}
x --;
y --;
q[0].init();
q[1].init();
memset(flag,0,sizeof(flag));
ss.pos = x * 3 + y;
ss.state = ss.step = 0;
q[0].push(ss);
flag[0][0][ss.pos] = 1;
dfs(8,0,0);//
if(flag[1][q[0].top().state][q[0].top().pos])
{
printf("0\n");
continue;
}
int ans = -1;
int t1,t2;
k = 0;
for(j = 0;j < d1 && ans < 0;j ++)
{
for(i = 0;i <= 1;i ++)//2个队列 0正向搜 1反向搜
{
while(!q[i].empty())// && q[i].top().step == j)
{
if(i)//反向
{
if(!(q[i].top().step == k && k < d2))
break;
}
else
{
if(!(q[i].top().step == j))
break;
}
now = q[i].top();
q[i].pop();
if(now.pos >= 3)//empty up
{
ss = now;
ss.step ++;
t1 = getdigit(now.state,10 - now.pos);
t2 = roll[t1][0];
ss.pos -= 3;
ss.state -= (t1 * fac[10 - now.pos]);//
t1 = getdigit(now.state,9 - now.pos);
ss.state -= (t1 * fac[9 - now.pos]);
ss.state += (t1 * fac[10 - now.pos]);
t1 = getdigit(now.state,8 - now.pos);
ss.state -= (t1 * fac[8 - now.pos]);
ss.state += (t1 * fac[9 - now.pos]);
ss.state += (t2 * fac[8 - now.pos]);//
if(!flag[i][ss.state][ss.pos])
{
flag[i][ss.state][ss.pos] = 1;
if(flag[1 - i][ss.state][ss.pos])
{
ans = i?j + k + 2:j + k + 1;
break;
}
q[i].push(ss);
}
}
if(now.pos <= 5)//empty down
{
ss = now;
ss.step ++;
ss.pos += 3;
t1 = getdigit(now.state,5 - now.pos);
t2 = roll[t1][0];
ss.state -= (t1 * fac[5 - now.pos]);
t1 = getdigit(now.state,6 - now.pos);
ss.state += (t1 * fac[5 - now.pos]);
ss.state -= (t1 * fac[6 - now.pos]);
t1 = getdigit(now.state,7 - now.pos);
ss.state += (t1 * fac[6 - now.pos]);
ss.state -= (t1 * fac[7 - now.pos]);
ss.state += (t2 * fac[7 - now.pos]);
if(!flag[i][ss.state][ss.pos])
{
flag[i][ss.state][ss.pos] = 1;
if(flag[1 - i][ss.state][ss.pos])
{
ans = i?j + k + 2:j + k + 1;
break;
}
q[i].push(ss);
}
}
if(now.pos % 3)//empty left
{
ss = now;
ss.step ++;
ss.pos --;
t1 = getdigit(now.state,8 - now.pos);
t2 = roll[t1][1];
ss.state -= (t1 * fac[8 - now.pos]);
ss.state += (t2 * fac[8 - now.pos]);
if(!flag[i][ss.state][ss.pos])
{
flag[i][ss.state][ss.pos] = 1;
if(flag[1 - i][ss.state][ss.pos])
{
ans = i?j + k + 2:j + k + 1;
break;
}
q[i].push(ss);
}
}
if((now.pos + 1) % 3)//empty right
{
ss = now;
ss.step ++;
ss.pos ++;
t1 = getdigit(now.state,7 - now.pos);
t2 = roll[t1][1];
ss.state -= (t1 * fac[7 - now.pos]);
ss.state += (t2 * fac[7 - now.pos]);
if(!flag[i][ss.state][ss.pos])
{
flag[i][ss.state][ss.pos] = 1;
if(flag[1 - i][ss.state][ss.pos])
{
ans = i?j + k + 2:j + k + 1;
break;
}
q[i].push(ss);
}
}
}
if(ans > 0)
break;
}
if(k < d2)
k ++;
}
printf("%d\n",ans);
}
return 0;
}
//正向12步 反向18步: .....
//正向13步 反向17步: Wrong Answer
//正向14步 反向16步: Wrong Answer
//正向15步 反向15步:56664K 4813MS
//正向16步 反向14步: 56892K 4000MS
//正向17步 反向13步: 57380K 2782MS
//正向18步 反向12步: 58192K 2016MS
//正向19步 反向11步: 51712K 1547MS
//正向20步 反向10步: 47212K 1282MS
//正向21步 反向9步: 45848K 1204MS 31340K 1204MS(循环队列开到100005)
//正向22步 反向8步: 47728K 1391MS
//正向23步 反向7步: 51968K 1704MS
//正向24步 反向6步: ...
//正向25步 反向5步: ...
/*
2 1
R B W
R W W
E W W
3 3
W B W
B R E
R B R
3 3
B W R
B W R
B E R
2 1
B B B
B R B
B R E
1 1
R R R
W W W
R R E
2 1
R R R
B W B
R R E
3 2
R R R
W E W
R R R
1 2
W W W
E W W
W W W
0 0
*/