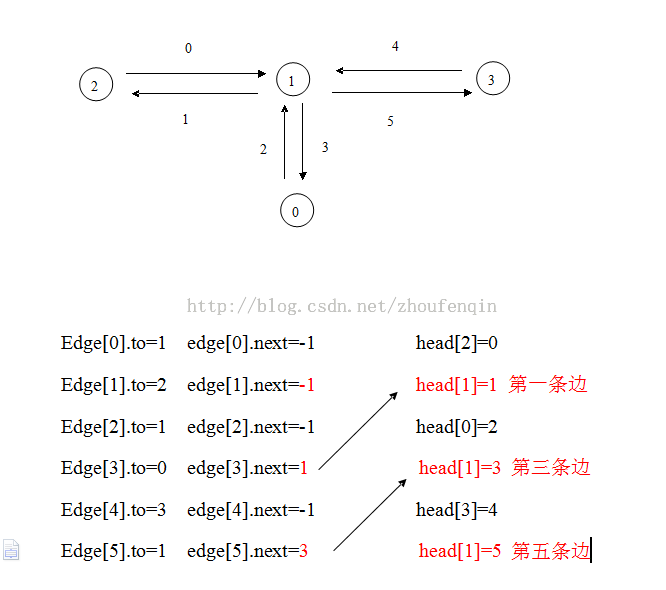
数的直径 hdu 4607Park Visit

这部分理论是在摘抄别人的~哈哈

树的直径(Diameter)是指树上的最长简单路。

直径的求法：两遍BFS (or DFS)

任选一点u为起点，对树进行BFS遍历，找出离u最远的点v，以v为起点，再进行BFS遍历，找出离v最远的点w。则v到w的路径长度即为树的直径

*简单证明

于是原问题可以在O(E)时间内求出关键在于证明第一次遍历的正确性，也就是对于任意点u，距离它最远的点v一定是最长路的一端。

如果u在最长路上，那么v一定是最长路的一端。可以用反证法：假设v不是最长路的一端，则存在另一点v’使得(u→v’)是最长路的一部分，于是len(u→v’) > len(u→v)。但这与条件“v是距u最远的点”矛盾。

如果u不在最长路上，则u到其距最远点v的路与最长路一定有一交点c，且(c→v)与最长路的后半段重合(why?)，即v一定是最长路的一端

因为是树是连通的，所以u必有一条路径c和最长路径L相交，len(c)>=1，L被分为两部分，一部分l1，一部分l2

假设第一次dfs过后，所求最长路径lu端不在L上，那么len（lu）>=len(c)+len(l1)（l1，l2对称，取l1或者l2都一样）

len(l2+c+lu)>len(l1+l2),矛盾.

以 hdu 4607 Park Visit 为例

首先如果k小于等于直径长度，那么答案为k−1。 
如果k大于直径长度，设直径长度为r，那么答案为r−1+(k−r)∗2。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>

using namespace std;

const int Maxn=100110;
int n,etot,vis[Maxn],dis[Maxn],head[Maxn];
struct node  
{
    int to;//某边从此节点指向的节点
    int next;//之前连接此节点的边的编号
}edge[Maxn*2];
void Add_edge(int u,int v)
{
    edge[etot].to=v;
    edge[etot].next=head[u];
    head[u]=etot++;
}
int dfs(int n)
{
    int v;
    for(int i=head[n];i!=-1;i=edge[i].next)
    {
        v=edge[i].to;
        if(!vis[v])
        {
            dis[v]=dis[n]+1;
            vis[v]=1;
            dfs(v);
        }
    }
}
int Max_len()
{
    int Max=-1,k=0;
    for(int i=0;i<n;i++)
    {
        if(dis[i]>Max)
            Max=dis[i],k=i;
    }
    return k;
}
int Get_Len()
{
    memset(vis,0,sizeof(vis));
    vis[0]=1;
    dis[0]=0;
    dfs(0);
    int k=Max_len();
    memset(vis,0,sizeof(vis));
    vis[k]=1;
    dis[k]=0;
    dfs(k);
    k=Max_len();
    return dis[k];
}
int main()
{
    int T,q,k,u,v;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&q);
        etot=0;
        memset(head,-1,sizeof(head));
        for(int i=0;i<n-1;i++)
        {
            scanf("%d%d",&u,&v);
            u--,v--;
            Add_edge(u,v);
            Add_edge(v,u);
        }
        int len=Get_Len();
        for(int i=0;i<q;i++)
        {
            scanf("%d",&k);
            if(k<=len+1)
                printf("%d\n",k-1);
            else
                printf("%d\n",len+(k-len-1)*2);
        }
    }
    return 0;
}