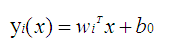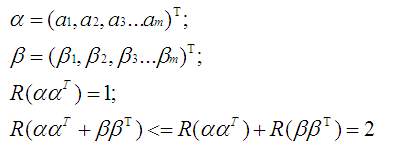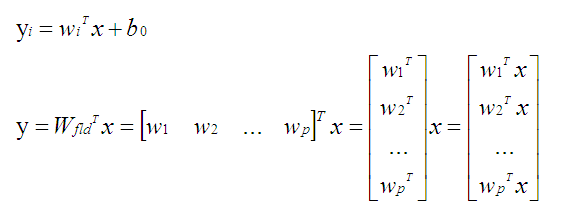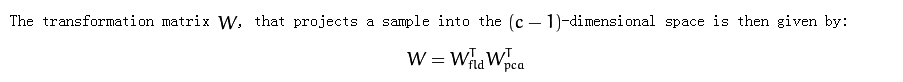LDA（线性判别分析或称Fisher线性判别）,PCA（主成份分析）代码及表情识别中的应用

【原文：http://blog.csdn.net/raby_gyl/article/details/20362373】

1、LDA线性判别分析

也称FLD（Fisher线性判别）是一种有监督的学习方法（supervised learning）。

LDA的基本思想是：

找到一个最佳的判别矢量空间，使得投影到该空间的样本的类间离散度与类内离散度比达到最大。

LDA的目的：

是从高维空间中提取出最优判别力的低维特征，这些特征使同一类别的样本尽可能的靠近，同时使不同类别的样本尽可能的分开，即选择使样本的类间散布矩阵和类内散布矩阵达到最大比值的特征。因此，用FLD得到的特征不但能够较好的表示原始数据，而且更适合分类。

LDA的两个基本用途：

降维和分类器（例如OpenCV中将LDA和K邻近分类器封装为一个“分类器”，这里K=1。所以本质还是降维和使数据易于可分）

LDA降维思想：

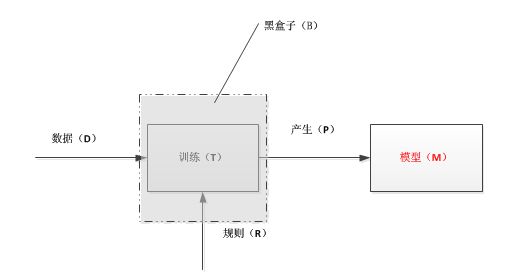
1）训练模型

数据(D):高维特征矢量

训练(T):操作模式

规则(R):训练数据的规则

黑盒子(B):如果我们只是想应用而不想理解其内部的复杂原理，我们可以不关系黑盒子里面是如何操作的。

模型(M):训练的结果，即产生(P)一个模型，这里是上面描述的一个矢量空间。

2）将高维数据送入模型实现降维

LDA分类器思想：

这里的分类思想，是OpenCV一种封装的分类思想，OpenCV在人脸识别算法中将LDA+1—邻近分类器组合，构造所谓的“合成分类器”，相当于类中的封装。

1）将所有训练样本图像投影到LDA子空间

2）将测试图像投影到LDA子空间

3）找到投影后的训练样本集和测试图像之间的最邻近，即如果测试图像与训练样本中的b最邻近，b属于C类，那么测试图像也属于C类。

LDA原理和计算过程：

LDA是一种线性分类器，它可以看作是SVM的简化版本。

正因为它是一种线性分类器，所以对于K-分类问题，有K-1个线性函数：

这个线性函数就是一个分类器。x是输出矢量，w是权重，y为输出值。对于两类，我们设置一个阈值y0,如果对于某些矢量x，带入到线性函数中的输出值y大与y0,则为一类，小于y0则为另一类。其实可以理解为：对于输入矢量x，这些矢量在一个多维 矢量空间中分布，wk就是一个权重，或者认为一个矢量空间，也或者认为是一个方向矢量，我们将x投影到矢量空间，或者说沿着这个方向上的投影后的值变为y,每一个矢量x对应投影后的一个值，对于不同的类别有不同的y值，或者y值范围，这使得数据变的更加容易可分。

注：关于类间离散度矩阵Sb的秩的参考理解（不是推导）：

例如：

对于二维点集的二分类问题。由于是二分类问题，那么上述公式3-36变为Wfld={W1}，p为1。那么利用公式3-37后的，y表示矢量x在w1方向的投影坐标。此时y数据的分布变的更加容易可分。

换角度理解：

我们知道Wlfd={w1,w2,w3,...,wp}，其中p<=C-1；

我们知道对于C类，如果用线性分类器进行分类的话，需要C-1个分类器。如对于两类，我们只需要一个分类函数，从中间劈开。

我们组合下面两个公式进行理解：

上述第一个公式表示为一个线性分类器，第二个公式表示p个线性分类器（这里的p取C-1)。

一个分类器可以对二类问题进行分类，那么第一个公式表示待分类矢量x经过投影变化后得到的y值更加容易可分。

p个分类器可以对p+1（即C）类问题进行分类，那么第二个公式表示待分类矢量x经过投影变化后得到矢量y更加容易可分。

LDA代码

OpenCV为我们实现了LDA类，我们只需要会使用就可以了。

LDA类的构造函数：

1、

//矩阵src以行存储训练样本矢量，行数表示训练样本的总数，列数表示样本矢量（特征矢量）的维数

//labels是与训练样本所对应的类别。此构造函数要求输入数据格式严格。

//参数num_components=0采用默认，由给定数据自动判决

 LDA(const Mat& src, vector<int> labels,int num_components = 0):_num_components(num_components)
        {
            this->compute(src, labels); //! compute eigenvectors and eigenvalues
        }

2、

//格式较为宽松的构造函数

//src可以是一个vector<Mat>，也可以是vector<vector>,我们一般选择第一种

//labels可以是Mat 一行或者一列存储着类的标号。

 LDA(InputArrayOfArrays src, InputArray labels,int num_components = 0) :
                     _num_components(num_components)
         {
             this->compute(src, labels); //! compute eigenvectors and eigenvalues
         }

LDA::project

//投影样本到LDA子空间

 // Projects samples into the LDA subspace.
 Mat LDA::project(InputArray src) {
    return subspaceProject(_eigenvectors, Mat(), _dataAsRow ? src : src.getMat().t());
 }

LDA::reconstruct

//重构来自于LDA子空间的投影

 // Reconstructs projections from the LDA subspace.
 Mat LDA::reconstruct(InputArray src) {
    return subspaceReconstruct(_eigenvectors, Mat(), _dataAsRow ? src : src.getMat().t());
 }

特征矢量和特征值的获取

 // Returns the eigenvectors of this LDA.
         Mat eigenvectors() const { return _eigenvectors; };

         // Returns the eigenvalues of this LDA.
         Mat eigenvalues() const { return _eigenvalues; }

对象的导入与导出

 // Serializes this object to a given filename.
 void save(const string& filename) const;

 // Deserializes this object from a given filename.
 void load(const string& filename);

 // Serializes this object to a given cv::FileStorage.
 void save(FileStorage& fs) const;

     // Deserializes this object from a given cv::FileStorage.
 void load(const FileStorage& node);

应用降维思路：

训练数据的处理：

1、循环读入训练图像Mat，并将Mat对象存储到vector<Mat>容器中，同时新建一个Mat对象，或行矢量或列矢量来存储类别标签。

2、将步骤1中的数据传入到LDA的构造函数中，构造函数进行计算处理，从而获得特征矢量。

3、将训练数据利用project函数，投影到特征矢量构造的子空间，即LDA子空间，将返回的Mat矢量保存起来，做后续的处理。

4、将LDA对象，利用save保存起来。

测试数据的处理：

1、利用load函数将LDA导入

2、利用project函数，将测试数据投影到LDA子空间，保存返回的Mat矢量，做后续的处理。

LDA其他知识

转换矩阵W，可以将样本投影到c-1维空间，其中c表示类别。

PCA对光照的灵敏度将高。LDA对光照不如PCA对光照的敏感。LDA的性能同样严重的依赖于输入的数据。

LDA也可以像PCA那样对图像进行重建，但是LDA重建效果没有PCA好，这是因为PCA利用的个体的主成份特征，而LDA利用了辨别个体之间不同的特征。

2、PCA——主成份分析

PCA又叫K-L变换，是一个无监督的学习方法。

PCA和LDA类似这里不在书写，网上资料也一大把。只给出几个连接：

1）PCA理论分析及应用

2）OpenCV PCA

3、PCA+LDA

Wfld表示LDA的特征矢量构成的，Wpca表示PCA的特征矢量构成的，u是PCA分析中所有样本的均值。z矢量的维数为类别数目-1.

4、应用：基于Gabor小波和PCA+FLD+最邻近分类的人脸表情识别

6种表情的Gabor特征下载地址（包括训练和测试）：http://download.csdn.net/detail/xuluhui123/6989241

思路：对提取的Gabor特征图像，即特征矢量利用PCA进行降维，将降维后的矢量送入到:

 Ptr<FaceRecognizer> model = createFisherFaceRecognizer();
    model->train(images, labels);
    // The following line predicts the label of a given
    // test image:
    int predictedLabel = model->predict(testSample);

Fisher人脸识别器集成了LDA+最邻近判别分类。

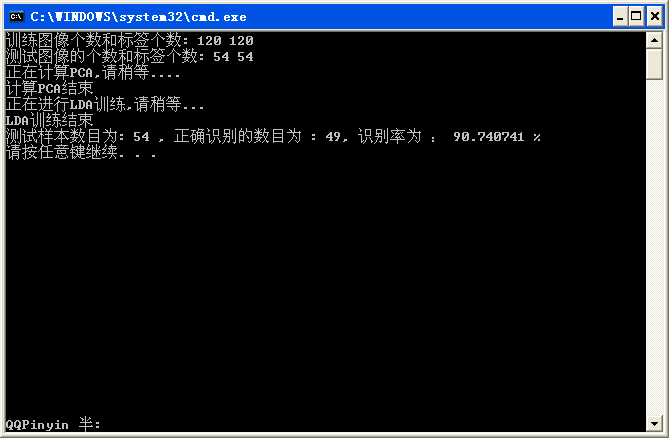
实验数据采用日本女人表情人脸库，对6种表情进行分类。训练数据：每类表情20个样本，共120个。测试数据：每类表情9个数据，共54个测试。

采用与人有关的方式进行测试。

程序如下：

 #include "opencv2/core/core.hpp"
 #include "opencv2/contrib/contrib.hpp"
 #include "opencv2/highgui/highgui.hpp"

 #include <iostream>
 #include <fstream>
 #include <sstream>

 using namespace cv;
 using namespace std;

 static Mat asRowMatrix(InputArrayOfArrays src, int rtype, double alpha=1, double beta=0);//vector<Mat> 到Mat 的转换

 int main(int argc, const char *argv[])
 {
     int i,j,k;
     string c_path="D:\\shuchugabor(测试)\\";//测试图像路径
     string x_path="D:\\shuchugabor(训练)\\";//训练图像路径
     vector<Mat> c_img;
     vector<Mat> x_img;
     vector<int> c_label;//存储类别标签
     vector<int> x_label;

     for(i=1;i<7;i++)
     {
         for(j=1;j<21;j++)//每类采用20个作为训练
         {
             string s1,s2;
             stringstream ss1,ss2;
             ss1<<i;ss2<<j;
             ss1>>s1;ss2>>s2;
             string cs_path=c_path+s1+"("+s2+").tiff";
             string xl_path=x_path+s1+"("+s2+").tiff";

             Mat xl_img=imread(xl_path.c_str(),0);
             x_img.push_back(xl_img);
             x_label.push_back(i);
             if(j<10)//每类采用9个进行测试
             {
                 Mat cs_img=imread(cs_path.c_str(),0);
                 c_img.push_back(cs_img);
                 c_label.push_back(i);
             }

         }
     }
 #if 1
     cout<<"训练图像个数和标签个数: "<<x_img.size()<<" "<<x_label.size()<<endl;
     cout<<"测试图像的个数和标签个数: "<<c_img.size()<<" "<<c_label.size()<<endl;

 #endif

     Mat x_mat=asRowMatrix(x_img,CV_32FC1);//转化为Mat同时转化为float类型

     cout<<"正在计算PCA,请稍等...."<<endl;
     PCA pca(x_mat,Mat(),0);//均值由PCA计算，0表示样本特征以行形式排列
     cout<<"计算PCA结束"<<endl;

     vector<Mat> x_pca;//存储投影后的矢量
     vector<Mat> c_pca;

     //cout<<pca.eigenvectors.rows<<" "<<pca.eigenvectors.cols<<endl;

     for(i=0;i<x_img.size();i++)
     {
         Mat x_temp(x_img[0].rows,x_img[0].cols,x_img[0].type());
         x_img[i].copyTo(x_temp);
         x_pca.push_back(pca.project(x_temp.reshape(1,1)));
     }

     for(i=0;i<c_img.size();i++)
     {
         Mat c_temp(c_img[0].rows,c_img[0].cols,c_img[0].type());
         c_img[i].copyTo(c_temp);
         c_pca.push_back(pca.project(c_temp.reshape(1,1)));
     }

     Ptr<FaceRecognizer> model=createFisherFaceRecognizer();
     cout<<"正在进行LDA训练,请稍等..."<<endl;
     model->train(x_pca,x_label);
     cout<<"LDA训练结束"<<endl;

     int t_num=0;
     for(i=0;i<c_pca.size();i++)
     {
         int predictedLabel=model->predict(c_pca[i]);
         //printf("预测是 %d ,实际是 %d \n",predictedLabel,c_label[i]);
         if(predictedLabel==c_label[i])
         {
             t_num++;
         }
     }

     printf("测试样本数目为: %d , 正确识别的数目为 : %d, 识别率为 ： %f %% \n",c_pca.size(),t_num,t_num/(float)c_pca.size()*100);

     return 0;

 }
 static Mat asRowMatrix(InputArrayOfArrays src, int rtype, double alpha, double beta) {
     // make sure the input data is a vector of matrices or vector of vector
     if(src.kind() != _InputArray::STD_VECTOR_MAT && src.kind() != _InputArray::STD_VECTOR_VECTOR) {
         string error_message = "The data is expected as InputArray::STD_VECTOR_MAT (a std::vector<Mat>) or _InputArray::STD_VECTOR_VECTOR (a std::vector< vector<...> >).";
         CV_Error(CV_StsBadArg, error_message);
     }
     // number of samples
     size_t n = src.total();
     // return empty matrix if no matrices given
     if(n == 0)
         return Mat();
     // dimensionality of (reshaped) samples
     size_t d = src.getMat(0).total();
     // create data matrix
     Mat data((int)n, (int)d, rtype);
     // now copy data
     for(unsigned int i = 0; i < n; i++) {
         // make sure data can be reshaped, throw exception if not!
         if(src.getMat(i).total() != d) {
             string error_message = format("Wrong number of elements in matrix #%d! Expected %d was %d.", i, d, src.getMat(i).total());
             CV_Error(CV_StsBadArg, error_message);
         }
         // get a hold of the current row
         Mat xi = data.row(i);
         // make reshape happy by cloning for non-continuous matrices
         if(src.getMat(i).isContinuous()) {
             src.getMat(i).reshape(1, 1).convertTo(xi, rtype, alpha, beta);
         } else {
             src.getMat(i).clone().reshape(1, 1).convertTo(xi, rtype, alpha, beta);
         }
     }
     return data;
 }

执行结果：

参考资料：

1、基于Gabor小波变换和SVM的人脸表情识别  王黎艳

2、机器学习中的数学(4)-线性判别分析(LDA),主成份分析(PCA)

3、LDA详解包括OpenCV代码实现

4、使用OpenCV进行人脸识别的的三种算法。

5、http://docs.opencv.org/modules/contrib/doc/facerec/facerec_tutorial.html

6、PCA理论分析及应用

7、OpenCV PCA