HDU 3265 Posters(线段树:扫描线)
HDU 3265 Posters(线段树:扫描线)
http://acm.hdu.edu.cn/showproblem.php?pid=3265
题意:
给你N个中间镂空了一个小矩形洞的大矩形,然后问你这些矩形的整体面积(矩形平行与坐标轴且重叠部分只算一次)?
分析:
这道题目WA了我很久,我一开始想用之前的模板直接套用的,不过有很多细节没处理好,结果捷径没走成还是错漏百出.
首先本题与HDU1542很相似,可以用几乎一样的基本方法解决.
http://blog.csdn.net/u013480600/article/details/22548393
需要注意的地方是,这里的矩形还有个小矩形洞,所以我们在读大矩形下位边时+1,上位边时-1.但是我们读入小矩形(大矩形中空的部分)时,小矩形的下位边cnt-1,上位边cnt+1.
这样我们就能完全模拟出之前的效果了,不过不能用HDU1828的那种cnt信息位不上传也不下放的方式了,这里必须PushDown和PushUp了.
经过测试上面,发现上面的方法测试的几组实例正确但是超时了.
因为cnt信息要上传下传,结果cnt信息分成了很多块,所以超时了.(这里很有意思,我原本的nodes数组应该开4*MAXN大小的,但是我只开了MAXN大小,但是OJ不提示存取越界而是提示WA,然后我把nodes改成了4倍大小后,OJ提示超时.)
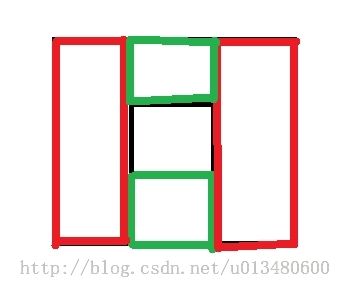
下面用HDU1828的老方法做,不过这里要注意nodes节点要开8倍MAXN的大小.还有处理方式是这样的,比如说下面的例子:
我们的处理方式是:
将上面的空心矩形分成4个不空心的矩形即可,不过记得nodes要开8倍MAXN大小.
AC代码:
<span style="font-size:18px;">#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=55555;
#define lson i*2,l,m
#define rson i*2+1,m+1,r
int cnt[MAXN*4],sum[MAXN*4];
struct node
{
int l,r,h,d;
node(){}
node(int a,int b,int c,int d):l(a),r(b),h(c),d(d){}
bool operator < (const node & b)const
{
if (h == b.h) return d > b.d;//这句话不写也AC,但是还是写上保险,对于本题来说写不写没区别
return h<b.h;
}
}nodes[MAXN*8];
void PushUp(int i,int l,int r)
{
if(cnt[i])
sum[i]=r-l+1;
else if(l==r)
sum[i]=0;
else
sum[i]=sum[i*2]+sum[i*2+1];
}
void build(int i,int l,int r)
{
cnt[i]=0;
sum[i]=0;
if(l==r)
return ;
int m=(l+r)>>1;
build(lson);
build(rson);
//PushUp(i,l,r);
}
void update(int ql,int qr,int v,int i,int l,int r)
{
if(ql<=l&&r<=qr)
{
cnt[i]+=v;
PushUp(i,l,r);
return ;
}
int m=(l+r)>>1;//这里一定小心,如果是m=(l+r)/2,会无限递归,栈溢出,如ql=qr=-1且l=-1,r=0的时候
if(ql<=m) update(ql,qr,v,lson);
if(m<qr) update(ql,qr,v,rson);
PushUp(i,l,r);
}
int main()
{
int t;
while(scanf("%d",&t)==1&&t)
{
int m=0;
int lbd=50000,rbd=0;
for(int i=1;i<=t;i++)
{
int x1,y1,x2,y2,x3,y3,x4,y4;
scanf("%d%d%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
lbd=min(lbd,x1);
rbd=max(rbd,x2);
nodes[++m]= node(x1,x3,y1,1);
nodes[++m]= node(x1,x3,y2,-1);
nodes[++m]= node(x4,x2,y1,1);
nodes[++m]= node(x4,x2,y2,-1);
nodes[++m]= node(x3,x4,y1,1);
nodes[++m]= node(x3,x4,y3,-1);
nodes[++m]= node(x3,x4,y4,1);
nodes[++m]= node(x3,x4,y2,-1);
}
sort(nodes+1,nodes+m+1);
build(1,lbd,rbd-1);
long long ans=0;
for(int i=1;i<m;i++)
{
int ql=nodes[i].l;
int qr=nodes[i].r-1;
if(ql<=qr)update(ql,qr,nodes[i].d,1,lbd,rbd-1);
ans+= (long long)sum[1]*(nodes[i+1].h-nodes[i].h);
}
printf("%I64d\n",ans);
}
}
</span>
另外一种划分方式:
AC代码:
<span style="font-size:18px;">#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=55555;
#define lson i*2,l,m
#define rson i*2+1,m+1,r
int cnt[MAXN*4],sum[MAXN*4];
struct node
{
int l,r,h,d;
node(){}
node(int a,int b,int c,int d):l(a),r(b),h(c),d(d){}
bool operator < (const node & b)const
{
if (h == b.h) return d > b.d;//这句话不写也AC,但是还是写上保险,对于本题来说写不写没区别
return h<b.h;
}
}nodes[MAXN*8];
void PushUp(int i,int l,int r)
{
if(cnt[i])
sum[i]=r-l+1;
else if(l==r)
sum[i]=0;
else
sum[i]=sum[i*2]+sum[i*2+1];
}
void build(int i,int l,int r)
{
cnt[i]=0;
sum[i]=0;
if(l==r)
return ;
int m=(l+r)>>1;
build(lson);
build(rson);
//PushUp(i,l,r);
}
void update(int ql,int qr,int v,int i,int l,int r)
{
if(ql<=l&&r<=qr)
{
cnt[i]+=v;
PushUp(i,l,r);
return ;
}
int m=(l+r)>>1;//这里一定小心,如果是m=(l+r)/2,会无限递归,栈溢出,如ql=qr=-1且l=-1,r=0的时候
if(ql<=m) update(ql,qr,v,lson);
if(m<qr) update(ql,qr,v,rson);
PushUp(i,l,r);
}
int main()
{
int t;
while(scanf("%d",&t)==1&&t)
{
int m=0;
int lbd=50000,rbd=0;
for(int i=1;i<=t;i++)
{
int x1,y1,x2,y2,x3,y3,x4,y4;
scanf("%d%d%d%d%d%d%d%d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
lbd=min(lbd,x1);
rbd=max(rbd,x2);
nodes[++m]= node(x1,x2,y1,1);
nodes[++m]= node(x1,x2,y3,-1);
nodes[++m]= node(x1,x3,y3,1);
nodes[++m]= node(x1,x3,y2,-1);
nodes[++m]= node(x4,x2,y3,1);
nodes[++m]= node(x4,x2,y2,-1);
nodes[++m]= node(x3,x4,y4,1);
nodes[++m]= node(x3,x4,y2,-1);
}
sort(nodes+1,nodes+m+1);
build(1,lbd,rbd-1);
long long ans=0;
for(int i=1;i<m;i++)
{
int ql=nodes[i].l;
int qr=nodes[i].r-1;
if(ql<=qr)update(ql,qr,nodes[i].d,1,lbd,rbd-1);
ans+= (long long)sum[1]*(nodes[i+1].h-nodes[i].h);
}
printf("%I64d\n",ans);
}
}
</span>