第一题：无限序列（提高组第一试2011年10月21日）（2011年NOIP冲刺模拟试题）

    【问题描述】

我们按以下方式产生序列：

1、开始时序列是："1" ；

2、每一次变化把序列中的"1"变成"10"，"0" 变成 "1"。

经过无限次变化，我们得到序列"1011010110110101101..."。

总共有Q个询问，每次询问为：在区间A和B之间有多少个1。

任务：写一个程序回答Q个询问。 

【输入】

第一行为一个整数Q，后面有Q行，每行两个数用空格隔开的整数a, b。 

【输出】

共Q行，每行一个回答。 

【样例输入】

1

2 8 

【样例输出】

4 

【数据范围】

对于30%的数据，1<=Q<=20，1<=a<=b<10000；

对于100%的数据，1<=Q<=5000，1<=a<=b<2^63；

 

我们先看看序列变化规律，S1 = "1", S2 = "10", S3 = "101", S4 = "10110", S5 = "10110101", 等等. Si 是 S（i+1）的前缀。

序列Si 是由序列 S（i-1） 和 S（i-2）, 连接而成的。

即Si = S（i-1）+S（i-2）(实际上是Fibonacci数列)。

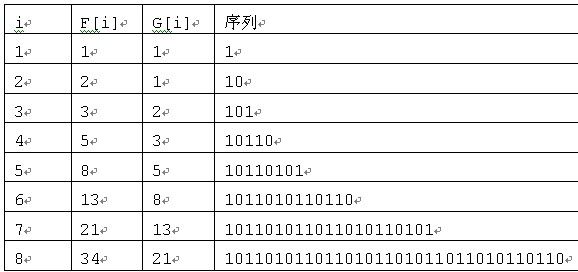
设F[i]表示第i个序列的（长度）位数，G[i]表示第i个序列中“1”的个数。 如果要求的区间端点恰好是某个F[i]，则可以直接返回此时的G[i]。例如，当a=1,b=13时，F[6]=13，则序列中G[6]=8个“1”。如果区间的端点不是某个F[i], 需要发现的规律是:如果a=F[i]+F[j]+F[k]，则区间[1，a]中“1”的个数为G[i]+G[j]+G[k]。

例如，a=31时，a=F[7]+F[5]+F[2]=21+8+2，则区间中“1”的个数为：

               13 + 5 + 1 = 19

找到规律后，我们可以用递归的方法求出任意长度的序列中“1”的个数。在计算闭区间[a, b]中“1”的个数时，用区间[1,b]的结果减去区间[1,a-1]的结果。这是一个常用的技巧。

我们先看看序列变化规律，S1 = "1", S2 = "10", S3 = "101", S4 = "10110", S5 = "10110101", 等等. Si 是 S（i+1）的前缀。

序列Si 是由序列 S（i-1） 和 S（i-2）, 连接而成的。

即Si = Si-1 + Si-2 (实际上是Fibonacci数列)。

设F[i]表示第i个序列的（长度）位数，G[i]表示第i个序列中“1”的个数。 如果要求的区间端点恰好是某个F[i]，则可以直接返回此时的G[i]。例如，当a=1,b=13时，F[6]=13，则序列中G[6]=8个“1”。如果区间的端点不是某个F[i],mj 需要发现的规律是:如果a=F[i]+F[j]+F[k]，则区间[1，a]中“1”的个数为G[i]+G[j]+G[k]。

例如，a=31时，a=F[7]+F[5]+F[2]=21+8+2，则区间中“1”的个数为：

               13 + 5 + 1 = 19

找到规律以后，我们可以用递归的方法求出任意长度的序列中“1”的个数。在计算闭区间[a, b]中“1”的个数时，是用区间[1,b]的结果减去区间[1,a-1]的结果。这是一个常用的技巧，希望能记着用。

我的代码：

/******************************************************************************************************
 ** Copyright (C) 2011.07.01-2013.07.01
 ** Author: famousDT <[email protected]>
 ** Edit date: 2011-10-23
******************************************************************************************************/
#include <stdio.h>
#include <stdlib.h>//abs,atof(string to float),atoi,atol,atoll
#include <math.h>//atan,acos,asin,atan2(a,b)(a/b atan),ceil,floor,cos,exp(x)(e^x),fabs,log(for E),log10
#include <vector>
#include <queue>
#include <map>
#include <time.h>
#include <set>
#include <list>
#include <stack> 
#include <string>
#include <iostream>
#include <assert.h>
#include <string.h>//memcpy(to,from,count
#include <ctype.h>//character process:isalpha,isdigit,islower,tolower,isblank,iscntrl,isprll
#include <algorithm>
using namespace std;

typedef unsigned long long ll;

#define MY_PI acos(-1)
#define MY_MAX(a, b) ((a) > (b) ? (a) : (b))
#define MY_MIN(a, b) ((a) < (b) ? (a) : (b))
#define MY_MALLOC(n, type) ((type *)malloc((n) * sizeof(type)))
#define MY_ABS(a) (((a) >= 0) ? (a) : (-(a)))
#define MY_INT_MAX 0x7fffffff
#define LOW_BIT(a) ((a) & (-(a)))//last none zero value

/*==========================================================*\
| 
\*==========================================================*/
#define MAX 100 - 8
ll x[MAX],y[MAX];
ll process(ll a, ll carry)
{
	if (a == 0) return 0;
	if (a == x[carry]) return y[carry];
	if (a < x[carry]) return process(a, --carry);
	return process(a - x[carry], carry - 2) + y[carry];
}
int main()
{
    FILE *in, *out;
    in = fopen("infinit.in", "rt");
    out = fopen("infinit.out", "wt");
	ll a, b;
	int i;
	x[1] = 1;
	x[2] = 2;
	y[1] = y[2] = 1;
	for (i = 3; i <= MAX; ++i) {
		x[i] = x[i - 1] + x[i - 2];
		y[i] = y[i - 1] + y[i - 2];
		//printf("%25llu%25llu\n", x[i], y[i]);
	}
	//printf("%25.0lf\n", pow(2.0, 63) - 1);//9223372036854775800
	int q;
	scanf("%d", &q);
	while (q--) {
		scanf("%llu%llu", &a, &b);
		ll ans = process(b, MAX - 1) - process(a - 1, MAX - 1);
		printf("%llu\n", ans);
	}
    fclose(in);
    fclose(out);
    return 0;
}