高斯混合模型(GMM)介绍以及学习笔记
1.高斯混合模型概述
高斯密度函数估计是一种参数化模型。高斯混合模型(Gaussian Mixture Model, GMM)是单一高斯概率密度函数的延伸,GMM能够平滑地近似任意形状的密度分布。高斯混合模型种类有单高斯模型(Single Gaussian Model, SGM)和高斯混合模型(Gaussian Mixture Model, GMM)两类。类似于聚类,根据高斯概率密度函数(Probability Density Function, PDF)参数不同,每一个高斯模型可以看作一种类别,输入一个样本x,即可通过PDF计算其值,然后通过一个阈值来判断该样本是否属于高斯模型。很明显,SGM适合于仅有两类别问题的划分,而GMM由于具有多个模型,划分更为精细,适用于多类别的划分,可以应用于复杂对象建模。
1.1.单高斯模型
多维高斯(正态)分布概率密度函数PDF定义如下:

注意与一维高斯分布不同,其中x是维数为d的样本向量(列向量), 是模型期望,∑是模型方差。
对于单高斯模型,由于可以明确训练样本是否属于该高斯模型,故 通常由训练样本均值代替,∑由样本方差代替。为了将高斯分布用于模式分类,假设训练样本属于类别C,那么,式(1)可以改为如下形式:
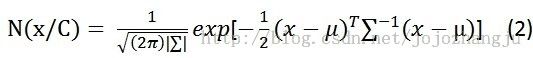
式子(2)表明样本属于类别C的概率大小。从而将任意测试样本![]() 输入式(2),均可以得到一个标量
输入式(2),均可以得到一个标量![]() ,然后根据阈值t来确定该样本是否属于该类别。
,然后根据阈值t来确定该样本是否属于该类别。
*阈值t的确定:可以为经验值,也可以通过实验确定。另外也有一些策略可以参考,如:首先令t=0.7,以0.05为步长一直减到0.1左右,选择使样本变化最小的那个阈值做为最终t值,也就是意味着所选的t值所构造的分类模型最稳定。
*几何意义理解:单高斯分布模型在二维空间应该近似于椭圆,在三维空间上近似于椭球。遗憾的是在很多分类问题中,属于同一类别的样本点并不满足“椭圆”分布的特性。这就引入了高斯混合模型。
1.2.高斯混合模型
高斯混合模型是单一高斯机率密度函数的延伸,由于 GMM 能够平滑地近似任意形状的密度分布,因此近年来常被用在语音、图像识别等方面,得到不错的效果。
例如:例:有一批观察数据 数据个数为n,在d维空间中的分布不是椭球状(如图1(a)),那么就不适合以一个单一的高斯密度函数来描述这些数据点的机率密度函数。此时我们采用一个变通方案,假设每个点均由一个单高斯分布生成(如图1(b),具体参数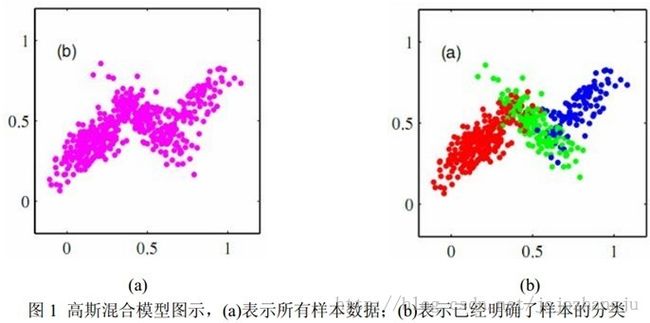
从数学上讲,我们认为这些数据的概率分布密度函数可以通过加权函数表示:
表示第j个SGM的PDF。
j需要实现确定好,就像K-means中的K一样。 是权值因子。其中的任意一个高斯分布GMM是一种聚类算法,每个component就是一个聚类中心。即在只有样本点,不知道样本分类(含有隐含变量)的情况下,计算出模型参数
这显然可以用EM算法来求解。再用训练好的模型去差别样本所属的分类,方法是:
Step1:随机选择K个component中的一个(被选中的概率是Step2:把样本代入刚选好的component,判断是否属于这个类别,如果不属于则回到step1
2.高斯混合模型参数估计
2.1样本分类已知情况下的GMM
当每个样本所属分类已知时,GMM的参数非常好确定,直接利用Maximum Likelihood。设样本容量为N,属于K个分类的样本数量分别是![]() ,属于第k个分类的样本集合是L(k)
,属于第k个分类的样本集合是L(k)
2.2.样本分类未知情况下的GMM
有N个数据点,服从某种分布![]() ,我们想要找到一组参数
,我们想要找到一组参数![]() ,使得生成这些数据点的概率最大,这个概率就是:
,使得生成这些数据点的概率最大,这个概率就是:
称为似然函数(Likelihood Function)。通常单个点的概率很小,连乘之后数据会更小,容易造成浮点数下溢,所以一般取对数,变成:
称为log-likelihood function。
GMM的log-likelihood function就是:
这里每个样本所属的类别是不知道的。Z是隐含变量。
我们就是要找到最佳的模型参数,使得(10)式所示的期望最大,“期望最大化算法”名字由此而来。
EM法求解:
EM要求解的问题一般形式是:
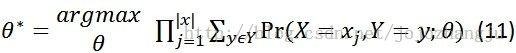
Y是隐含变量,我们已经知道如果数据点的分类标签Y是已知的,那么求解模型参数直接利用Maximum Likelihood就可以了。EM算法的基本思路是:随机初始化一组参数![]() 根据后验概率
根据后验概率![]() 来更新Y的期望E(Y),然后用E(Y)代替Y求出新的模型参数
来更新Y的期望E(Y),然后用E(Y)代替Y求出新的模型参数![]() 。如此迭代直到
。如此迭代直到![]() 趋于稳定。
趋于稳定。
E-Step E就是Expectation的意思,就是假设模型参数已知的情况下求隐含变量Z分别取![]() 的期望,亦即Z分别取
的期望,亦即Z分别取![]() 的概率。在GMM中就是求数据点由各个 component生成的概率。
的概率。在GMM中就是求数据点由各个 component生成的概率。
![]()
注意到我们在Z的后验概率前面乘以了一个权值因子,它表示在训练集中数据点属于类别![]() 的频率,在GMM中它就是
的频率,在GMM中它就是![]() 。
。
M-StepM就是Maximization的意思,就是用最大似然的方法求出模型参数。现在我们认为上一步求出的![]() 就是“数据点由component k生成的概率”。根据公式(5),(6),(7)可以推出:
就是“数据点由component k生成的概率”。根据公式(5),(6),(7)可以推出: