妹子问题 --动态规划问题
看HMM中间遇到动态规划问题。
动态规划的最优路径如何解释呢?举这个例子吧,从上海到武汉需要经过很多城市(苏州 —— 常州 —— 南京 —— 合肥 —— 麻城 ——— 武汉)。每个经过的城市可以从不同的收费站经过。这样就有很多选择的路线。假设每个收费站的收费标准不同。我们想选一条最优路线,交出的路费最少。你怎么选?有人说,呵呵,这个简单吗,把每个城市收费最少的收费站挑出来,这不就是最少的收费吗?这个就是上面的近似算法。把每个局部最少的选出来一拼接不就OK的,错了,为什么?你没考虑他们这些收费站之间的联系。现在苏州收费最少的是苏州东,收100块吧。无锡最少的收费是无锡南,收120吧。你的最优路径就是应该就是 苏州东 —— 无锡南—— ………… 可惜的是,他们之间没有路。我想这就是这个算法最大的缺点。
那怎么办呢?
====算法A:
我们这么想想,现在,假设地图上海到武汉有三座中间的城市 A B C,他们各自分别有三个收费站A1, A2, A3, B1, B2……还可以继续假A 到 B, B 到 C各自的三站两两都有通路(已经不是上述的近似算法问题,这个假设可以存在)。
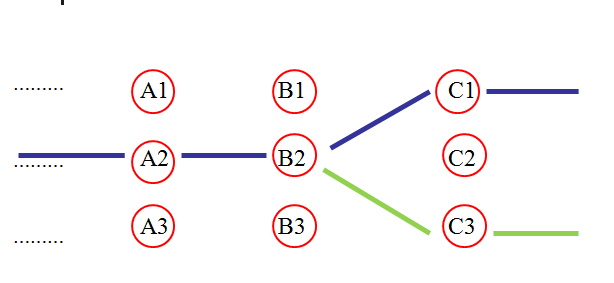
假设现在 :我们已经知道交费最少的路径是通过B的时候是这么样的——紫色的路线。
那么能否说 从城市B的B2出发到武汉的交费最少路线是B2右边边那个紫色的路线?
答案是肯定的。
假设,到B2到武汉有个交费更少的路线(下面的那个浅绿色路线)。那么,我敢保证,上面说的这个紫色全程路线肯定不是交费最少的。因为B2左边面的交费一样多,右边从下面走更便宜,我完全可以先到B2,然后走B2右下边的浅绿色路线。这么花费更少么?
所以,假设全程最优的路径经过B2,那么B2右边的那个路径就是B2到武汉最优的路径。
====算法A结束
====算法B
知道这个能干什么呢?我们可以这样求出最优的路径。从上海出发开始,递推的计算出到达常州啊,南京啊等城市的各个站口交费最少路径(疑问A:不是只求某个,是到该城市所有的站口的最少收费。有几个站口,就有各自最少收费,为什么呢,后面有例子)。直至推到武汉。比较最后的交费发现,有条路线从苏州的苏州西出发,到武汉东交出的路费最少。现在需要知道具体的路线。那好,根据上面的算法A,依次倒着(麻城,合肥 ……)将最优路线经过的每个城市的收费站推算出来。
====算法B结束
====算法C
现在,问题是顺着计算话怎么递推出到各个城市的各个收费站交费最少路径。
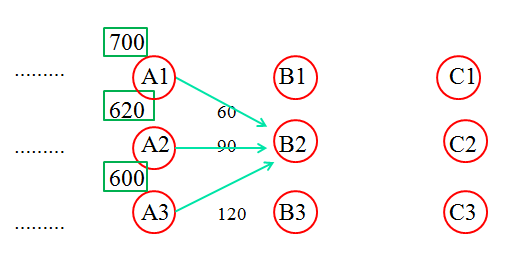
看图。假设到城市A的三个收费站A1 A2 A3最少交费已经求出,分别是700, 620, 600。现在计算到城市B 中 B2收费站交费最少的路线。
那么从 A1 到 B2 的费用为 700 + 60 = 760
A2 到 B2 的费用为620 + 90 = 710
A3 到 B2 的费用为600 + 120 = 720
所以从上海到B城市的B2 最少收费是 经过A2 这个路线。费用是710。然后可以这么类似的计算出 到 B1,B3的最优路线。(疑问A可以解答,到A最优是A3,但到B最优可能不是经过A3,到最终的路线也可能不经过A3)
这样就可以从A中各个收费站最优路线计算出B城市中各个收费站最优路线。一次次往后迭代直到算出到武汉各个收费站的最少收费。从各个收费站收费间选出某个收费最少的路线。然后使用算法B,可以将这个最优的路线求出来。求得的结果是(上海出发 —— 苏州某收费站 —— 常州某收费站 —— 南京某收费站 —— 合肥某收费站 —— 麻城某收费站 ——— 武汉某收费站——到武汉 )。
====算法C结束
*上述实验数据中全是捏造,如有雷同,纯属巧合。