hdu1401Solitaire(dbfs)

Solitaire

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2539    Accepted Submission(s): 826

Problem Description

Solitaire is a game played on a chessboard 8x8. The rows and columns of the chessboard are numbered from 1 to 8, from the top to the bottom and from left to right respectively.

There are four identical pieces on the board. In one move it is allowed to:

> move a piece to an empty neighboring field (up, down, left or right),

> jump over one neighboring piece to an empty field (up, down, left or right). 



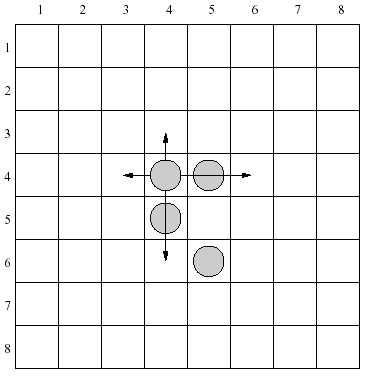
There are 4 moves allowed for each piece in the configuration shown above. As an example let's consider a piece placed in the row 4, column 4. It can be moved one row up, two rows down, one column left or two columns right.

Write a program that:

> reads two chessboard configurations from the standard input,

> verifies whether the second one is reachable from the first one in at most 8 moves,

> writes the result to the standard output.

 

Input

Each of two input lines contains 8 integers a1, a2, ..., a8 separated by single spaces and describes one configuration of pieces on the chessboard. Integers a2j-1 and a2j (1 <= j <= 4) describe the position of one piece - the row number and the column number respectively. Process to the end of file.

 

Output

The output should contain one word for each test case - YES if a configuration described in the second input line is reachable from the configuration described in the first input line in at most 8 moves, or one word NO otherwise.

 

Sample Input

   
   
   
   

    
    
    
    4 4 4 5 5 4 6 5
2 4 3 3 3 6 4 6
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    YES
   
   
   
   

 

Source

Southwestern Europe 2002

 

Recommend

Ignatius.L

唉，这题从昨晚调到现在，结果被自己一个sb错误坑了这么久，强烈bs一下自己。。。

题目大意：一个8*8的棋盘上面有4颗棋子，4颗棋子都一样。每颗棋子可以向周围4个方向移动，如果相邻的地方没有其他棋子，可以移动到相邻位置，如果相邻位置已经有棋子了，并且相邻位置的棋子同方向的相邻位置没有棋子，则也可以移动。具体看图就明白。现在给定初态和终态，判断8步内是否能从初态到终态。

题目分析：bfs。由于本题状态实在太多，单向bfs肯定会爆内存。而且本题给了终态，很自然想到dbfs。判重的话，由于有4颗棋子，所以状态非常多。没有想到比较好的判重方式。所以就开了一个4维数组判重。将每颗棋子的坐标化成一个0-63的整数，然后开一个四维数组判重。这样的代价比较大。然后就按照一般的dbfs开始写。写完交了几遍都MLE了。。。因为是同时从两边开始搜的，所以数组要开2个，一个数组的规模64^4大概在一千万以上，而且同时搜2个队列同时工作，空间开销非常之大。于是又重写了一下。这次用2次单向bfs，分别从起点和终点搜4步。开一个四维数组判重即可。具体做法是用2-5标识正向搜4步的所有到达的状态。7-10标识反向搜4步能到达的所有状态。0表示正反都未搜过。那么在搜索的时候如果正向搜，所有的状态标记上，反向搜的时候如果发现某个状态已经被标记了，检查标记是否小于6，如果是，则表明正向已经到达这个状态了，返回。如果正反4步都没搜到，返回。

昨晚调到今天，结果跪在了返回条件上。因为正向是从1开始搜的，要控制搜4步，那么出队的节点的step要<=5。。。少了2个等号。。。悲剧这么久。。。

这题还要注意的是判重的时候要对点的位置排序，因为移动后点的位置编号就乱了，很多情况是一个状态，如果步排序就会增加很多状态。

详情请见代码(还是比较臭比较长但是比较清晰):D

#include <iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 10005;//减掉2个0  62MS	16736K
char flag[64][64][64][64];
bool ok;

struct node
{
    int pos[4];
    char step;
}ss,now;

struct que
{
    struct node t[N];
    int head,tail;
    void init()
    {
        head = tail = 0;
    }
    bool empty()
    {
        return tail == head;
    }
    struct node top()
    {
        return t[head];
    }
    void push(struct node a)
    {
        t[tail] = a;
        tail ++;
        if(tail >= N)
            tail -= N;
    }
    void pop()
    {
        head ++;
        if(head >= N)
            head -= N;
    }
}q;

bool find(int x)
{
    int i;
    for(i = 0;i < 4;i ++)
        if(ss.pos[i] == x)
            return true;
    return false;
}

void bfs(int time)
{
    int i;
    while(!q.empty())
    {
        now = q.top();
        if(!time && now.step >= 5)//!!!不加等号就会多搜一步
        {
            return;
        }
        if(time && now.step >= 10)//!!!
        {
            return;
        }
        q.pop();
        for(i = 0;i < 4;i ++)
        {
            ss = now;
            ss.step ++;
            if(ss.pos[i] >= 8 && !find(ss.pos[i] - 8))//up
                ss.pos[i] -= 8;
            else
            {
                if(ss.pos[i] >= 16 && !find(ss.pos[i] - 16) && find(ss.pos[i] - 8))
                    ss.pos[i] -= 16;
            }
            sort(ss.pos,ss.pos + 4);
            if(!flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]])
            {
                flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] = ss.step;
                q.push(ss);
            }
            else
            {
                if(time && flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] < 6)
                {
                    ok = true;
                    return;
                }
            }

            ss = now;
            ss.step ++;
            if(ss.pos[i] <= 55 && !find(ss.pos[i] + 8))//down
                ss.pos[i] += 8;
            else
            {
                if(ss.pos[i] <= 47 && !find(ss.pos[i] + 16) && find(ss.pos[i] + 8))
                    ss.pos[i] += 16;
            }
            sort(ss.pos,ss.pos + 4);
            if(!flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]])
            {
                flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] = ss.step;
                q.push(ss);
            }
            else
            {
                if(time && flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] < 6)
                {
                    ok = true;
                    return;
                }
            }

            ss = now;
            ss.step ++;
            if(ss.pos[i] % 8 && !find(ss.pos[i] - 1))
                ss.pos[i] -= 1;
            else
            {
                if(ss.pos[i] % 8 > 1 && !find(ss.pos[i] - 2) && find(ss.pos[i] - 1))
                    ss.pos[i] -= 2;
            }
            sort(ss.pos,ss.pos + 4);
            if(!flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]])
            {
                flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] = ss.step;
                q.push(ss);
            }
            else
            {
                if(time && flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] < 6)
                {
                    ok = true;
                    return;
                }
            }

            ss = now;
            ss.step ++;
            if((ss.pos[i]) % 8 != 7 && !find(ss.pos[i] + 1))
                ss.pos[i] += 1;
            else
            {
                if(ss.pos[i] % 8 < 6 && !find(ss.pos[i] + 2) && find(ss.pos[i] + 1))
                    ss.pos[i] += 2;
            }
            sort(ss.pos,ss.pos + 4);
            if(!flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]])
            {
                flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] = ss.step;
                q.push(ss);
            }
            else
            {
                if(time && flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] < 6)
                {
                    ok = true;
                    return;
                }
            }
        }
    }
}

int main()
{
    int a,b;
    int i;
    while(scanf("%d%d",&a,&b)!= EOF)
    {
        ss.pos[0] = (a - 1) * 8 + b - 1;
        for(i = 1;i < 4;i ++)
        {
            scanf("%d%d",&a,&b);
            ss.pos[i] = (a - 1) * 8 + b - 1;
        }
        memset(flag,0,sizeof(flag));
        sort(ss.pos,ss.pos + 4);
        flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] = 1;
        ss.step = 1;
        q.init();
        ok = false;
        q.push(ss);
        bfs(0);
        for(i = 0;i < 4;i ++)
        {
            scanf("%d%d",&a,&b);
            ss.pos[i] = (a - 1) * 8 + b - 1;
        }
        sort(ss.pos,ss.pos + 4);
        ss.step = 6;
        if(flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]])
        {
            printf("YES\n");
            continue;
        }
        else
            flag[ss.pos[0]][ss.pos[1]][ss.pos[2]][ss.pos[3]] = 6;
        q.init();
        q.push(ss);
        bfs(1);
        if(ok)
            printf("YES\n");
        else
            printf("NO\n");    
    }
    return 0;
}
//78MS	16740K