求朋友圈个数
假如已知有n个人和m对好友关系(存于数字r)。如果两个人是直接或间接的好友(好友的好友的好友...),则认为他们属于同一个朋友圈,请写程序求出这n个人里一共有多少个朋友圈。
假如:n = 5 , m = 3 , r = {{1 , 2} , {2 , 3} , {4 , 5}},表示有5个人,1和2是好友,2和3是好友,4和5是好友,则1、2、3属于一个朋友圈,4、5属于另一个朋友圈,结果为2个朋友圈。
#include <stdio.h>
int set[10] = {0};
int find(int a)
{
int r,i,j;
r = a;
while(r != set[r])
r = set[r];
i = a;
while(i != r)
{
j = set[i];
set[i] = r;
i = j;
}
return r;
}
void merge(int a, int b)
{
int a_father = find(a);
int b_father = find(b);
if(a_father == b_father)
return;
else if(a_father < b_father)
set[b_father] = a_father;
else
set[a_father] = b_father;
}
int friends(int n, int m, int r[][2])
{
int i,count=0;
for(i=0;i<n;i++)
set[i] = i;
for(i=0;i<m;i++)
merge(r[i][0],r[i][1]);
for(i=0;i<n;i++)
if(set[i] == i)
count++;
return count;
}
int main()
{
int n=5,m=3,count=0,i;
int r[3][2] = {{1,2},{2,3},{4,5}};
printf("朋友圈关系:\n");
for(i=0;i<3;i++)
printf("%d,%d\t",r[i][0],r[i][1]);
printf("\n");
count = friends(n,m,r);
printf("朋友圈个数为:\n%d\n",count);
return 0;
}
以下是并查集简单介绍,摘自http://blog.sina.com.cn/s/blog_65f3869301011abb.html
并查集是一种树型的数据结构,用于处理不相交集合的合并和查询问题,速度很快,有很多应用,其中kruskal算法最为广泛。
并查集的三个基本操作:
1. makeSet():初始化每一个元素都各自为一个独立的集合,可以让每个元素的祖先为-1(parent[x] = -1)或者为自身(parent[x] = x),视自身喜好而定。
2. findSet(x):找到元素所在的集合,也就是找到自己的最高的祖先,这也是判断两个元素是否在同一个集合中的主要依据
3. unionSet(x, y):将x和y所在的集合进行合并,利用findSet()判断x和y所在的集合是否相同,如果不同,则要把其中一个元素的祖先
指向另一个元素的祖先。
用一张很流行的图来简单说一下。如下图所示:开始的时候有{c、h、b、e}和{f、d、g}两个集合,c和f分别为两个集合的最高祖先,
经过合并之后,把c也指向了f,这样形成了一棵树。
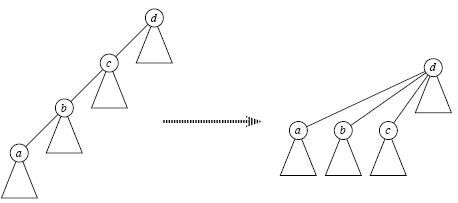
但是这时候问题就来了,如果查找b的祖先,需要沿着b -> h -> c -> f这条路径一直向上爬,是一个O(n)的时间复杂度,这就引出
了路径压缩优化。就是在findSet的时候利用递归顺便把经过的点的祖先直接修改成最高祖先。比如下图执行过findSet(a)之后就
可以将b和c的祖先修改成d,下次再查找的时候就不用慢慢向上爬了。