Wiki OI 1039 数的划分
题目链接:http://wikioi.com/problem/1039/
算法与思路:划分型dp,递推;
将整数n分成k份,且每份不能为空,任意两份不能相同(不考虑顺序)。例如:n=7,k=3,下面三种分法被认为是相同的。
1,1,5; 1,5,1; 5,1,1;
因此将n划分份的一种方法唯一的表示为n1+n2+……nk,其中n1<=n2<=….nk.
这样可以形象地把n的k份划分看作是把n块积木堆成k列,且每列的积木块数依次递增,
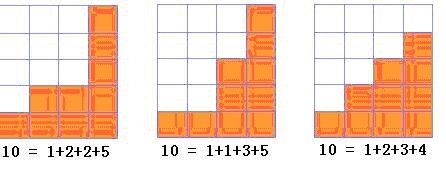
也就是这n块积木从左到右被堆成了“阶梯状”。比如,下图是10的几种划分方法:
把上图的三个矩形顺时针旋转90度后,如下图:
不难发现,选转之后的模型还是10的划分,不过约束条件有所不同。
很明显,由于原来是k份划分,因此新的模型中的最大一个元素必然是k。
而其余的元素大小不限,但都不能大于k. n减去k后,n’=n-k, 剩下的问题就是求n’的任意划分,
且其中每个元素都不大于k的方案总数了。
新模型中,n的k份剖分的一种分法表示为n块积木从右到左递增排列,其中最左列有k块积木。
两个模型中对n的k份剖分的每种分法表示是一一对应的,如:
10=1+2+2+5 对应 10=4+3+1+1+1
10=1+1+3+5 对应 10=4+2+2+1+1
10=1+2+3+4 对应 10=4+3+2+1
因此,求n的k份划分的方案总数问题转化为根据新模型将n做任意划分,且其中最大的一个部分恰好是k的问题。
求解这个新的模型可以用递推的方法,用f (a,b)表示把b做任意份剖分,
其中最大的一个部分等于a的方案总数,用g(a,b)表示把b做任意份划分,
其中最大的一个部分不大于a的方案总数,则有:
f (a, b) = g (a, b - a);
g(a, b) = f(1, b) + f(2, b) +...+ f(a, b);
又因为
f(1, b) + f(2, b) +...+ f(a - 1, b) = g(a - 1, b);
所以
g(a, b) = f(1, b) +...+ f(a - 1, b) +f(a, b)
= g(a - 1, b) + g(a, b - a) (1 <= i <= a - 1)
当b < a时,根据g(a, b)的含义,g(a, b - a)无意义。
当a = 1时,显然 g(1, b) = 1.
g(1, b) = 1
g (a - 1, b) + g(a, b - a) (b >= a)
g (a, b) = g (a - 1, b) (b < a)
最后的g (k, n - k)即为所求。
#include<stdio.h>
#include<string.h>
int main()
{
int n, k, g[10][205];
while(scanf("%d%d", &n, &k) != EOF)
{
memset(g, 0, sizeof(g));
for(int j = 0; j <= n; j++)
g[1][j] = 1;
for(int i = 2; i <= k; i++)
for(int j = 0; j <= n - k; j++)
if(j >= i)
g[i][j] = g[i - 1][j] + g[i][j - i];
else
g[i][j] = g[i - 1][j];
printf("%d\n", g[k][n - k]);
}
}