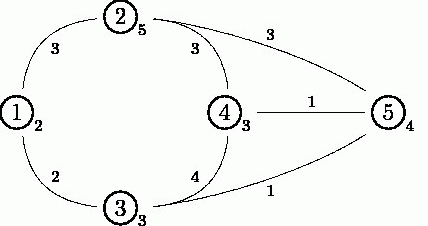
 从草地1到草地3的道路的“边过路费”为3,草地2的“点过路费”为5。 要从草地1走到草地4,可以从草地1走到草地3再走到草地5最后抵达草地4。如果这么走的话, 需要的“边过路费”为2+1+1=4,需要的点过路费为4(草地5的点过路费最大),所以总的花 费为4+4=8。 而从草地2到草地3的最佳路径是从草地2出发,抵达草地5,最后到达草地3。这么走的话,边 过路费为3+1=4,点过路费为5,总花费为4+5=9。
从草地1到草地3的道路的“边过路费”为3,草地2的“点过路费”为5。 要从草地1走到草地4,可以从草地1走到草地3再走到草地5最后抵达草地4。如果这么走的话, 需要的“边过路费”为2+1+1=4,需要的点过路费为4(草地5的点过路费最大),所以总的花 费为4+4=8。 而从草地2到草地3的最佳路径是从草地2出发,抵达草地5,最后到达草地3。这么走的话,边 过路费为3+1=4,点过路费为5,总花费为4+5=9。
bzoj1774【Usaco2009 Dec】Toll 过路费
1774: [Usaco2009 Dec]Toll 过路费
Time Limit: 10 Sec Memory Limit: 64 MBSubmit: 285 Solved: 172
[ Submit][ Status][ Discuss]
Description
跟所有人一样,农夫约翰以着宁教我负天下牛,休叫天下牛负我的伟大精神,日日夜夜苦思生 财之道。为了发财,他设置了一系列的规章制度,使得任何一只奶牛在农场中的道路行走,都 要向农夫约翰上交过路费。 农场中由N(1 <= N <= 250)片草地(标号为1到N),并且有M(1 <= M <= 10000)条 双向道路连接草地A_j和B_j(1 <= A_j <= N; 1 <= B_j <= N)。奶牛们从任意一片草 地出发可以抵达任意一片的草地。FJ已经在连接A_j和B_j的双向道路上设置一个过路费L_j (1 <= L_j <= 100,000)。 可能有多条道路连接相同的两片草地,但是不存在一条道路连接一片草地和这片草地本身。最 值得庆幸的是,奶牛从任意一篇草地出发,经过一系列的路径,总是可以抵达其它的任意一片 草地。 除了贪得无厌,叫兽都不知道该说什么好。FJ竟然在每片草地上面也设置了一个过路费C_i (1 <= C_i <= 100000)。从一片草地到另外一片草地的费用,是经过的所有道路的过路 费之和,加上经过的所有的草地(包括起点和终点)的过路费的最大值。 任劳任怨的牛们希望去调查一下她们应该选择那一条路径。她们要你写一个程序,接受K(1 <= K <= 10,000)个问题并且输出每个询问对应的最小花费。第i个问题包含两个数字s_i 和t_i(1 <= s_i <= N; 1 <= t_i <= N; s_i != t_i),表示起点和终点的草地。 考虑下面这个包含5片草地的样例图像:
 从草地1到草地3的道路的“边过路费”为3,草地2的“点过路费”为5。 要从草地1走到草地4,可以从草地1走到草地3再走到草地5最后抵达草地4。如果这么走的话, 需要的“边过路费”为2+1+1=4,需要的点过路费为4(草地5的点过路费最大),所以总的花 费为4+4=8。 而从草地2到草地3的最佳路径是从草地2出发,抵达草地5,最后到达草地3。这么走的话,边 过路费为3+1=4,点过路费为5,总花费为4+5=9。
从草地1到草地3的道路的“边过路费”为3,草地2的“点过路费”为5。 要从草地1走到草地4,可以从草地1走到草地3再走到草地5最后抵达草地4。如果这么走的话, 需要的“边过路费”为2+1+1=4,需要的点过路费为4(草地5的点过路费最大),所以总的花 费为4+4=8。 而从草地2到草地3的最佳路径是从草地2出发,抵达草地5,最后到达草地3。这么走的话,边 过路费为3+1=4,点过路费为5,总花费为4+5=9。
 从草地1到草地3的道路的“边过路费”为3,草地2的“点过路费”为5。 要从草地1走到草地4,可以从草地1走到草地3再走到草地5最后抵达草地4。如果这么走的话, 需要的“边过路费”为2+1+1=4,需要的点过路费为4(草地5的点过路费最大),所以总的花 费为4+4=8。 而从草地2到草地3的最佳路径是从草地2出发,抵达草地5,最后到达草地3。这么走的话,边 过路费为3+1=4,点过路费为5,总花费为4+5=9。
从草地1到草地3的道路的“边过路费”为3,草地2的“点过路费”为5。 要从草地1走到草地4,可以从草地1走到草地3再走到草地5最后抵达草地4。如果这么走的话, 需要的“边过路费”为2+1+1=4,需要的点过路费为4(草地5的点过路费最大),所以总的花 费为4+4=8。 而从草地2到草地3的最佳路径是从草地2出发,抵达草地5,最后到达草地3。这么走的话,边 过路费为3+1=4,点过路费为5,总花费为4+5=9。
Input
* 第1行: 三个空格隔开的整数: N, M和K * 第2到第N+1行: 第i+1行包含一个单独的整数: C_i * 第N+2到第N+M+1行: 第j+N+1行包含3个由空格隔开的整数: A_j, B_j和L_j * 第N+M+2倒第N+M+K+1行: 第i+N+M+1行表示第i个问题,包含两个由空格隔开的整数s_i 和t_i
Output
* 第1到第K行: 第i行包含一个单独的整数,表示从s_i到t_i的最小花费。
Sample Input
5 7 2
2
5
3
3
4
1 2 3
1 3 2
2 5 3
5 3 1
5 4 1
2 4 3
3 4 4
1 4
2 3
2
5
3
3
4
1 2 3
1 3 2
2 5 3
5 3 1
5 4 1
2 4 3
3 4 4
1 4
2 3
Sample Output
8
9
9
HINT
Source
Gold
n的范围只有250,支持O(n^3)的算法,又要求最短路径,所以自然而然(“自然而然”这四个字说的真违心……)地想到Floyd。
那么点权最大值怎么处理呢?只要把点权从大到小排序,重新编号,按这个顺序跑Floyd就好了。
这道题将所有点按点权排序使当前点权为最大(或最小)点权的方法很值得借鉴。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define LL long long
#define pa pair<int,int>
#define MAXN 255
#define INF 1000000000
using namespace std;
int n,m,q,w[MAXN],a[MAXN],x,y,z,f[MAXN][MAXN],g[MAXN][MAXN];
int read()
{
int ret=0,flag=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch==-1) flag=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();}
return ret*flag;
}
bool cmp(int tmp1,int tmp2)
{
return w[tmp1]<w[tmp2];
}
int main()
{
n=read();m=read();q=read();
F(i,1,n) F(j,1,n) f[i][j]=g[i][j]=INF;
F(i,1,n) f[i][i]=0;
F(i,1,n) w[i]=read();
F(i,1,m)
{
x=read();y=read();z=read();
f[x][y]=f[y][x]=min(f[x][y],z);
}
F(i,1,n) a[i]=i;
sort(a+1,a+n+1,cmp);
F(k,1,n) F(i,1,n) F(j,1,n)
{
f[a[i]][a[j]]=min(f[a[i]][a[j]],f[a[i]][a[k]]+f[a[k]][a[j]]);
g[a[i]][a[j]]=min(g[a[i]][a[j]],f[a[i]][a[j]]+max(max(w[a[i]],w[a[j]]),w[a[k]]));
}
F(i,1,q)
{
x=read();y=read();
printf("%d\n",g[x][y]);
}
}