对斐波那契数列（兔子数列）的学习

斐波那契数列指的是这样一个数列：1、1、2、3、5、8、13、21、…… 

如果设F(n）为该数列的第n项（n∈N+）。那么这句话可以写成如下形式：　　F(0) = 0，F(1)=1，F(n)=F(n-1)+F(n-2) (n≥2） ；

通项公式：F(n)=（√5/5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}

这样一个完全是自然数的数列，通项公式却是用无理数来表达的。

性质：

     1.当n趋向于无穷大时，后一项与前一项的比值的小数部分越来越逼近黄金分割0.618。

     2.从第二项开始，每个奇数项的平方都比前后两项之积多1，每个偶数项的平方都比前后两项之积少1。

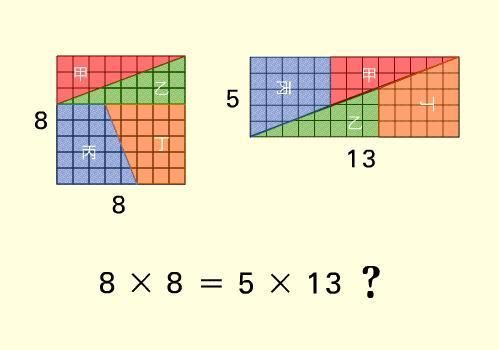
   一个有趣的游戏：

为什么64=65？其实就是利用了斐波那契数列的这个性质：5、8、13正是数列中相邻的三项，事实上前后两块的面积确实差1，只不过后面那个图中有一条细长的狭缝，一般人不容易注意到。

    3斐波那契数列的第n项同时也代表了集合{1,2,...,n}中所有不包含相邻正整数的子集个数。

　4.斐波那契数列（f(n），f(0)=0，f(1)=1，f(2)=1，f(3)=2……）的其他性质：

　　  1.f(0)+f(1)+f(2)+…+f(n)=f(n+2)-1。

　　 2.f(1)+f(3)+f(5)+…+f(2n-1)=f(2n）。

　　 3.f(2)+f(4)+f(6)+…+f(2n) =f(2n+1)-1。

　　 4.[f(0)]^2+[f(1)]^2+…+[f(n)]^2=f(n）·f(n+1）。

　　 5.f(0)-f(1)+f(2)-…+(-1)^n·f(n)=(-1)^n·[f(n+1)-f(n)]+1。

　　 6.f(m+n-1)=f(m-1）·f(n-1)+f(m）·f(n）。

斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”。

    一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔都不死，那么一年以后可以繁殖多少对兔子？

我们不妨拿新出生的一对小兔子分析一下：

第一个月小兔子没有繁殖能力，所以还是一对

两个月后，生下一对小兔民数共有两对

三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对

－－－－－－

依次类推可以列出下表：　　

经过月数	0	1	2	3	4	5	6	7	8	9	10	11	12
幼仔对数	1	0	1	1	2	3	5	8	13	21	34	55	89
成兔对数	0	1	1	2	3	5	8	13	21	34	55	89	144
总体对数	1	1	2	3	5	8	13	21	34	55	89	144	233

幼仔对数=前月成兔对数

成兔对数=前月成兔对数+前月幼仔对数

总体对数=本月成兔对数+本月幼仔对数

可以看出幼仔对数、成兔对数、总体对数都构成了一个数列。这个数列有关十分明显的特点，那是：前面相邻两项之和，构成了后一项。

c++中的斐波那契数列问题：

//输出一个斐波那契数列
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{   
    unsigned int val;
    cout<<"输入一个数，将输出不大于这个数的斐波那契数列："<<endl;
cin>>val;
if(val>4294967295||val<=0){
	cout<<"溢出，请输入0~4294967296之间的数"<<endl;
	return 0; 
}
unsigned int x=0,y=1,z,cont=1;
z=x+y;
cout<<setw(12)<<1;
while(z<=val){
cout<<setw(12)<<z<<" ";
x=y;
y=z;
z=x+y; 
cont++;
if(cont%6==0)
cout<<endl;   //每六个数字一行 
}
cout<<endl;
return 0;
}

上面那个受限，再来个很大长度的，也就是大数的时候：

//输出一个斐波那契数列
#include <iostream>
#include<string>
#include <iomanip>
using namespace std;
string add(string s1,string s2)
{
    
    int j,l,la,lb;
    string max,min;
    max=s1;min=s2;
    if(s1.length()<s2.length()) {max=s2;min=s1;}
    la=max.size();lb=min.size();
    l=la-1;
    for(j=lb-1;j>=0;j--,l--) max[l] += min[j]-'0'; 
    for(j=la-1;j>=1;j--) if(max[j]>'9'){max[j]-=10;max[j-1]++;}
    if(max[0]>'9') {max[0]-=10;max='1'+max;}
    return max;
}
int main()
{   
    string val;
    cout<<"输入一个数，将输出不大于这个数的斐波那契数列："<<endl;
    cin>>val;
    int cont=1;
    string x="0",y="1",z;
    z=add(x,y);
	cout<<"1"<<endl;
	while(z.length()<val.length()||(z.length()==val.length()&&z<val)){
	cout<<z<<endl;
	x=y;
	y=z;
	z=add(x,y); 
	}
	cout<<endl;
	return 0;
}