[置顶] 矩阵
数 aij(ij为下标)位于矩阵A的 i行j列,称为矩阵A的(i,j)位置的元素(简称为元), 记作 (aij)
或
![[置顶] 矩阵_第2张图片](http://img.e-com-net.com/image/info5/a141c56c5b694ee3af24bc136f025488.jpg)
· 元素为实数叫 实矩阵。有元素为复数则叫 复矩阵
· 行数和列数都等于n的矩阵,叫n阶矩阵 或 n阶方阵: An
· 只有一行的矩阵A=(a1, a2, ..., an) 称为 行矩阵、行向量
· 只有一列的矩阵 称为 列矩阵、列向量
· 若两个矩阵行列相等,即称为 同型矩阵
A=(aij),B=(bij),若aij=bij (i=1,2,...,m;j=1,2,...,n) => A=B
· 元素都为零的 称作 零矩阵 记作0. 注意不同型的0矩阵是不同的
· 像这样从左上到右下对角线(即主对角线)上的元素为1,其它都为0的方阵,称作单位矩阵 E
单位矩阵中的元素aij={1, 当i=j;0,当i≠j}
· 不在主对角线上的元素都为0(对角线上的元素为任意值),这样的方阵称为 对角矩阵
A=diag(a1,a2,...,an)
· 主对角元素都相等的对角矩阵,称为 数量矩阵,也称纯量阵
· aij=aji 的方阵,称为 对称矩阵 如:
· aij=-aji 的方阵, 称为 反对称矩阵 如:
用代码验证了下:
int a = 33, b = 38;//角度 double r = 10; //op长度 double acos = Math.cos(Math.PI/180 * a); double bcos = Math.cos(Math.PI/180 * b); double asin = Math.sin(Math.PI/180 * a); double bsin = Math.sin(Math.PI/180 * b); //x= System.out.println((acos*bcos - asin * bsin) * r); System.out.println(Math.cos(Math.PI / 180 * (a + b)) * r); //y= System.out.println((acos*bsin + asin * bcos) * r ); System.out.println(Math.sin(Math.PI / 180 * (a + b)) * r);
矩阵的运算
· 加法。 同型矩阵 才能相加。 A+B=B+A。运算时:(aij)+(bij)。 A-B = A+(-B)。A+(-A)=0 (0型矩阵)
· 矩阵与数相乘。 运算时:λ*A =λ乘以A中的每一项(aij)。
若有数x、y,矩阵A、B:(xy)A=x(yA);(x+y)A=xA+yA;x(A+B)=xA+xB
矩阵相加与数乘矩阵 统称为 矩阵的线性运算
· 矩阵乘矩阵。AB相乘,乘号左边矩阵的列要等于右边矩阵的行,才能相乘。A列等于B行。
乘积矩阵AB=C的(i,j)元cij就是A的i行与B的j列的乘积之和
(AB)C=A(BC);
k(AB)=(kA)B=A(kB); (k为数)
A(B+C)=AB+AC,(B+C)A=BA+CA;
AB≠BA;
乘单位矩阵E:AE=EA=A
kE即是纯量阵。(kE)A=k(EA)=kA,A(kE)=AkE=kAE=kA
若A为n阶方阵时, (kE)A=kA=A(kE); 这时可以交换。因AE都是n阶方阵,且E为纯量阵,所以只有第ixi可以相乘,这时AE=EA
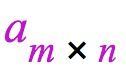
![[置顶] 矩阵_第1张图片](http://img.e-com-net.com/image/info5/43fa0edaefc8479a95c63b8d11536ace.jpg)
![[置顶] 矩阵_第3张图片](http://img.e-com-net.com/image/info5/e37fd4e5347742368c525e00dd74896c.jpg)
![[置顶] 矩阵_第4张图片](http://img.e-com-net.com/image/info5/d2e3efb985cc4afaa98923cead4e920e.jpg)