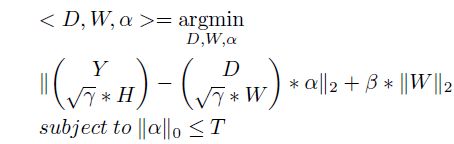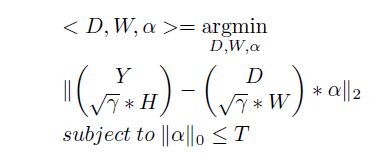D-KSVD（Discrimination K-SVD）

一、概述  

本文主要是对SRC算法的改进而介绍D-KSVD算法。由于SRC在字典学习时，选取训练集中的训练样本作为字典来进行编码，由此可能产生的问题有：字典过大，导致实验进行时运算量大耗时过长；字典原子未经过处理可能存在噪声；利用未经处理的训练样本作为字典原子，可能无法得到不同类样本所蕴含的深沉的区别点。但是SRC的优点是能够比较好点体现出字典的识别力。针对SRC的缺点，很自然的能想到字典学习的常用方法K-SVD，但是K-SVD训练的字典似乎丧失了识别力，因为此字典是一个公用的字典与SRC由不同类形成的小字典组合成的字典不同。于是提出了在K-SVD中加入一个线性分类器已解决字典低识别力的情况。

二、K-SVD介绍 

网上有很多博客对K-SVD的介绍推荐本人认为比较好的博客:(http://blog.csdn.net/abcjennifer/article/details/8693342)这篇博客对K-SVD的思路给出了一个通俗易懂的解释。  

想要进一步了解K-SVD的话可以看看Michael Elad 与2006年IEEE上发表的论文:（K-SVD: An Algorithm for Designing Overcomplete）链接地址如下：(Dictionaries%20for%20Sparse%20Representationhttp://www.cs.technion.ac.il/~freddy/papers/120.pdf)

三、线性分类器介绍（linear classifiers） 

分类器的作用是：根据特征提取器得到的特征向量来给一个被测对象赋予一个类标。线性分类器使用线性判别函数，其主要方法是：C类问题可以定义C个线性判别函数：

-------------------------------------------  

问题的关键是怎么利用训练集得到比较好Wi和wio。  

本文提出的线性分类器（7）式如下：

------------------------------

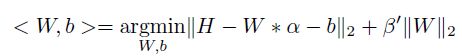
其中W是分类器矩阵，b是常数，H是样本标签。

四、D-KSVD模型介绍

模型公式（8）式：

-------------------------

--------------------------

相对于传统的K-SVD训练字典，此处加入一个线性分类器以达到所训练的字典具有识别能力。通俗一点来讲就是通过使得同一类样本的编码更相似，不同类样本的编码相似度大为降低，以达到提高所学习的字典的识别力的目的。

常用的求解步骤如下：

                                                                                           

               其中（5）式是（8）式去掉线性分类器部分余下的公式。以上步骤的第三和第四步采用梯度下降法。梯度下降法可能会陷入局部最优解。导致模型效果较差。对上式进行变形可得（注：此处变形只要将变形以后的公式展开就可的原式）：

                                                                                            

                由于D，W在训练开始时是以标准化进行的。于是能将上式中的正则项去除得到下式：

                                                                       

         对于此模型采用K-SVD算法就能进行求解。