矩阵分析中的LU分解

矩阵的因式分解是指把分解成两个或更多个矩阵的乘积，分解是指将分解成两个矩阵的乘法形式，即

假设是大小为  的矩阵，那么是的下三角矩阵，是  的上三角矩阵。

假设可以等价于某阶梯型矩阵，则存在单位下三角初等矩阵  使得

于是

其中

这里 表示矩阵取逆操作，显然有

对于线性方程组，倘若有 ，则有

即

令 ，则欲求，可先求 ，再求，如此则可降低运算复杂度。

以下是分解测试代码(C++)：

#include<cstdio>
#include<cmath>
#include<cassert>

class LUDec
{
public:
    
    void LU(double **A, int N, int M, double **L, double **U) {
        double **B = new double *[N]; assert(B != NULL);
        for(int i = 0; i < N; i ++) {
            B[i] = new double [M];
            assert(B[i] != NULL);
        }
        // init L & U and B
        for(int i = 0; i < N; i ++) {
            for(int j = 0; j < N; j ++) {
                L[i][j] = 0.0;
            }
            for(int j = 0; j < M; j ++) {
                U[i][j] = 0.0;
                B[i][j] = A[i][j];
            }
        }
        // please avoid abnormal data here
        for(int i = 0; i < N; i ++) {
            if( fabs(B[i][i]) < 1e-9 ) continue;
            for(int j = i + 1; j < N; j ++) {
                B[j][i] /= B[i][i];
                for(int k = i + 1; k < M; k ++)
                    B[j][k] -= B[j][i] * B[i][k];
            }
        }
        for(int i = 0; i < N; i ++) {
            L[i][i] = 1.0;
            for(int j = 0; j < M; j ++) {
                if( j < i )
                    L[i][j] = B[i][j];
                else
                    U[i][j] = B[i][j];
            }
        }
        if( B ) {
            for(int i = 0; i < N; i ++)
                delete[] B[i];
            delete[] B; B = NULL;
        }
    }
};

int main()
{
    LUDec cls;
    double **A = NULL, **L = NULL, **U = NULL;
    int N, M; scanf("%d %d", &N, &M); assert((N > 0 && N <= M)); // A: N x M
    A = new double *[N]; assert(A != NULL);
    for(int i = 0; i < N; i ++) {
        A[i] = new double [M];
        assert(A[i] != NULL);
    }
    // make sure that A can be LU-ed
    for(int i = 0; i < N; i ++) {
        for(int j = 0; j < M; j ++) {
            scanf("%lf", A[i] + j);
        }
    }
    L = new double *[N]; assert(L != NULL);
    for(int i = 0; i < N; i ++) {
        L[i] = new double [N];
        assert(L[i] != NULL);
    }
    U = new double *[N]; assert(U != NULL);
    for(int i = 0; i < N; i ++) {
        U[i] = new double [M];
        assert(U[i] != NULL);
    }
    cls.LU(A, N, M, L, U);
    printf("\nA = \n");
    for(int i = 0; i < N; i ++) {
        for(int j = 0; j < M; j ++)
            printf("%6.2lf", fabs(A[i][j]) < 0.005 ? 0 : A[i][j]);
        printf("\n");
    }
    printf("\nL = \n");
    for(int i = 0; i < N; i ++) {
        for(int j = 0; j < N; j ++)
            printf("%6.2lf", fabs(L[i][j]) < 0.005 ? 0 : L[i][j]);
        printf("\n");
    }
    printf("\nU = \n");
    for(int i = 0; i < N; i ++) {
        for(int j = 0; j < M; j ++)
            printf("%6.2lf", fabs(U[i][j]) < 0.005 ? 0 : U[i][j]);
        printf("\n");
    }
    if( A ) {
        for(int i = 0; i < N; i ++)
            delete[] A[i];
        delete[] A; A = NULL;
    }
    if( L ) {
        for(int i = 0; i < N; i ++)
            delete[] L[i];
        delete[] L; L = NULL;
    }
    if( U ) {
        for(int i = 0; i < N; i ++)
            delete[] U[i];
        delete[] U; U = NULL;
    }
    return 0;
}

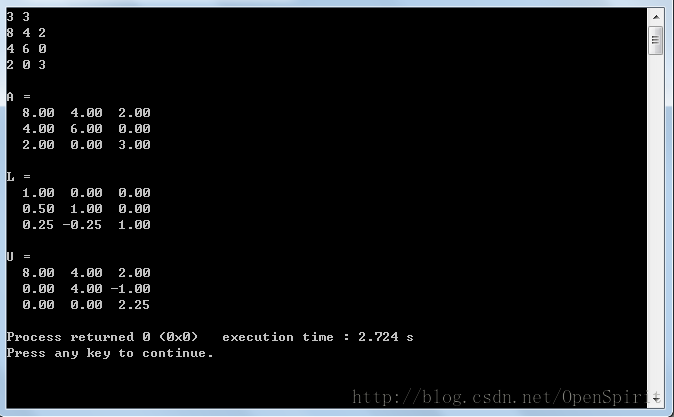
测试截图：