康托展开
康托展开
康托展开
{1,2,3,4,...,n}表示1,2,3,...,n的排列如 {1,2,3} 按从小到大排列一共6个 123 132 213 231 312 321
代表的数字 1 2 3 4 5 6 也就是把10进制数与一个排列对应起来。他们间的对应关系可由康托展开来找到。 如我想知道321是{1,2,3}中第几个大的数可以这样考虑 第一位是3,当第一位的数小于3时,那排列数小于321 如 123 213 小于3的数有1,2 所以有2*2!个 再看小于第二位2的 小于2的数只有一个就是1 所以有1*1!=1 所以小于321的{1,2,3}排列数有2*2!+1*1!=5个所以321是第6个大的数。 2*2!+1*1!是康托展开 再举个例子 1324是{1,2,3,4}排列数中第几个大的数 第一位是1小于1的数没有,是0个 0*3! 第二位是3小于3的数有1,2但1已经在第一位了所以只有一个数2 1*2! 第三位是2小于2的数是1,但1在第一位所以有0个数 0*1! 所以比1324小的排列有0*3!+1*2!+0*1!=2个 1324是第三个大数。
举例程序
- 应用于 USACO 3.2.5 Magic Squares (msquare) (翻译)(题解)
把一个8位的不重复八进制数字串进行康托展开
unsigned long cantor(unsigned long S) { long x=0,i,p,k,j; bool hash[8]={false}; for (i=8;i>=2;i--) { k=S>> 3*(i-1); S-=k<<3*(i-1); hash[k]=true; p=k; for (j=0;j<=k-1;j++) if (hash[j]) p--; x+=fac[i-1]*p; //fac存的是阶乘 fac[1] = 1, fac[2] = 2, fac[3] = 6... } return x; }
Function ct(p:arr):longint; Var i,j,t,ans:longint; Begin for i:=1 to 7 do //8位的时候 begin t:=0; for j:=i+1 to 8 do if p[j]<p[i] then inc(t); ans:=(ans+t)*(8-i); end; exit(ans); End;
康托展开[编辑]
康托展开是一个全排列到一个自然数的双射,常用于构建哈希表时的空间压缩。 康托展开的实质是计算当前排列在所有由小到大全排列中的顺序,因此是可逆的。
以下称第x个全排列是都是指由小到大的顺序。
目录
[隐藏]- 1 公式
- 1.1 举例
- 2 用途
- 3 康托展开的逆运算
- 4 参考文献
公式[编辑]
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!
其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。
a[i]的意义参见举例中的解释部分
举例[编辑]
例如,3 5 7 4 1 2 9 6 8 展开为 98884。因为X=2*8!+3*7!+4*6!+2*5!+0*4!+0*3!+2*2!+0*1!+0*0!=98884.
解释:
排列的第一位是3,比3小的数有两个,以这样的数开始的排列有8!个,因此第一项为2*8!
排列的第二位是5,比5小的数有1、2、3、4,由于3已经出现,因此共有3个比5小的数,这样的排列有7!个,因此第二项为3*7!
以此类推,直至0*0!
用途[编辑]
显然,n位(0~n-1)全排列后,其康托展开唯一且最大约为n!,因此可以由更小的空间来储存这些排列。由公式可将X逆推出对应的全排列。
康托展开的逆运算[编辑]
既然康托展开是一个双射,那么一定可以通过康托展开值求出原排列,即可以求出n的全排列中第x大排列。
如n=5,x=96时:
首先用96-1得到95,说明x之前有95个排列.(将此数本身减去!) 用95去除4! 得到3余23,说明有3个数比第1位小,所以第一位是4. 用23去除3! 得到3余5,说明有3个数比第2位小,所以是4,但是4已出现过,因此是5. 用5去除2!得到2余1,类似地,这一位是3. 用1去除1!得到1余0,这一位是2. 最后一位只能是1. 所以这个数是45321.
按以上方法可以得出通用的算法。
康托展开的公式是 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! 其中,ai为当前未出现的元素中是排在第几个(从0开始)。
这个公式可能看着让人头大,最好举个例子来说明一下。例如,有一个数组 s = ["A", "B", "C", "D"],它的一个排列 s1 = ["D", "B", "A", "C"],现在要把 s1 映射成 X。n 指的是数组的长度,也就是4,所以
X(s1) = a4*3! + a3*2! + a2*1! + a1*0!
关键问题是 a4、a3、a2 和 a1 等于啥?
a4 = "D" 这个元素在子数组 ["D", "B", "A", "C"] 中是第几大的元素。"A"是第0大的元素,"B"是第1大的元素,"C" 是第2大的元素,"D"是第3大的元素,所以 a4 = 3。
a3 = "B" 这个元素在子数组 ["B", "A", "C"] 中是第几大的元素。"A"是第0大的元素,"B"是第1大的元素,"C" 是第2大的元素,所以 a3 = 1。
a2 = "A" 这个元素在子数组 ["A", "C"] 中是第几大的元素。"A"是第0大的元素,"C"是第1大的元素,所以 a2 = 0。
a1 = "C" 这个元素在子数组 ["C"] 中是第几大的元素。"C" 是第0大的元素,所以 a1 = 0。(因为子数组只有1个元素,所以a1总是为0)
所以,X(s1) = 3*3! + 1*2! + 0*1! + 0*0! = 20
A B C | 0
A C B | 1
B A C | 2
B C A | 3
C A B | 4
C B A | 5
通过康托逆展开生成全排列
如果已知 s = ["A", "B", "C", "D"],X(s1) = 20,能否推出 s1 = ["D", "B", "A", "C"] 呢?
因为已知 X(s1) = a4*3! + a3*2! + a2*1! + a1*0! = 20,所以问题变成由 20 能否唯一地映射出一组 a4、a3、a2、a1?如果不考虑 ai 的取值范围,有
3*3! + 1*2! + 0*1! + 0*0! = 20
2*3! + 4*2! + 0*1! + 0*0! = 20
1*3! + 7*2! + 0*1! + 0*0! = 20
0*3! + 10*2! + 0*1! + 0*0! = 20
0*3! + 0*2! + 20*1! + 0*0! = 20
等等。但是满足 0 <= ai <= n-1 的只有第一组。可以使用辗转相除的方法得到 ai,如下图所示:
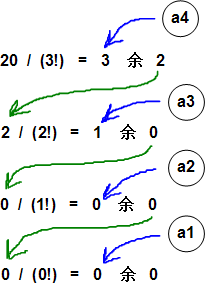
知道了a4、a3、a2、a1的值,就可以知道s1[0] 是子数组["A", "B", "C", "D"]中第3大的元素 "D",s1[1] 是子数组 ["A", "B", "C"] 中第1大的元素"B",s1[2] 是子数组 ["A", "C"] 中第0大的元素"A",s[3] 是子数组 ["C"] 中第0大的元素"C",所以s1 = ["D", "B", "A", "C"]。
这样我们就能写出一个函数 Permutation3(),它可以返回 s 的第 m 个排列。
前面的内容从http://archive.cnblogs.com/a/2026276/转载
- #include<iostream>
- #include<algorithm>
- #include<vector>
- #include<cstdlib>
- using namespace std;
- class cantor{
- public:
- int n;//字符串的长度
- string s;
- int pos;//字符串在全排列中的字典位置,从0开始
- vector<int>num;//所有的字符
- cantor(string s):s(s){n=s.size();}
- cantor(int n,int pos):n(n),pos(pos){
- int i;
- for(i=0;i<n;i++)
- num.push_back(i);
- }
- int fac(int);
- void encode();
- void decode();
- };
- int cantor::fac(int num){
- if(num==0) return 1;
- else return num*fac(num-1);
- }
- void cantor::encode(){
- int i,j,count;
- vector<int>vec(n);
- for(i=0;i<n;i++){
- count=0;
- for(j=i;j<n;j++)
- if(s[i]>s[j]) count++;
- vec[n-i-1]=count;
- }
- pos=0;
- for(i=0;i<s.size();i++)
- pos+=vec[i]*fac(i);
- }
- void cantor::decode(){
- int i;
- div_t divresult;
- for(i=n-1;i>=0;i--){
- divresult=div(pos,fac(i));求余数与除数
- s.push_back(num[divresult.quot]+'0');
- num.erase(num.begin()+divresult.quot);
- pos=divresult.rem;
- }
- }
- int main(){
- cantor test(4,2);
- test.decode();
- cout<<test.s<<endl;
- }
hdu1430魔板(BFS+康托展开)
做这题先看:http://blog.csdn.net/u010372095/article/details/9904497
1 2 3 4
8 7 6 5
对于魔板,可施加三种不同的操作,具体操作方法如下:
A: 上下两行互换,如上图可变换为状态87654321
B: 每行同时循环右移一格,如上图可变换为41236785
C: 中间4个方块顺时针旋转一格,如上图可变换为17245368
给你魔板的初始状态与目标状态,请给出由初态到目态变换数最少的变换步骤,若有多种变换方案则取字典序最小的那种。
12345678 17245368 12345678 82754631
C AC
for( i=0;i<8;i++)
pos[ch1[i]-'0']=i+1+'0';
for( i=0;i<8;i++)
des[i]=pos[str[i]-'0‘];
s=cantor(des);
上面一段代码的意思是:把起始目标看成了1,2,3,4,5,6,7,8 ;
列如:位置:12345678 12345678
起初: 63728145 变 12345678
终点: 86372541 成 51234876
解释一下:初:6在第1个位,那么在终点中找6用1代替,3在第2个位,在终点中找3用2代替,依次类推。
一开始我们就先按 12345678 这样的顺序建立了一棵像树一样的,如果直接从初态不进行转变的话,那么我们的结果可能有很多的走法,有可能是先走A或B都可以到目标,有多条路时,但是先走了B的路径,必须要输出小的也就是从A开始的那条路,那怎么办呢,就可以用转化的思想了,把初始状态变成12345678,这样的话,我们一开始就是从这样的顺序算出来的!!所以必须先进行转换,在从目标往上找并记下路径,一直找到最终父节点:12345678.
- #include<stdio.h>
- #include<iostream>
- #include<queue>
- #include<stack>
- #include<string.h>
- using namespace std;
- typedef struct nn
- {
- char ch[9];
- int son;
- }node1;
- typedef struct n
- {
- char way;//记录从父节点到当前节点的走法
- int father;//记录当前节点的父节点的位置
- }node2;
- node2 Node[40321];//节点
- int fac[8]={1,1,2,6,24,120,720,5040};//阶层
- int cantor(char s[])//计算s在康托展开的位置,每一个都是独一无二的
- {
- int i,j,k,ans=0;
- for(i=0;i<8;i++)
- {
- k=0;
- for(j=i+1;j<8;j++)
- if(s[i]>s[j])
- k++;
- ans+=k*fac[7-i];
- }
- return ans;
- }
- void BFS(char ch1[])
- {
- queue<node1>Q;
- node1 now,next;
- int i,son,e=0;
- char tc;
- son=cantor(ch1);
- strcpy(now.ch,ch1);now.ch[8]='\0';
- now.son=son;Node[son].father=0;//最终父节点为本本身
- Q.push(now);
- while(!Q.empty())
- {
- now=Q.front(); Q.pop();
- //printf("%s ",now.ch);if(e==300)getchar();e++;用于调试
- next=now;
- for(i=0;i<4;i++) {tc=next.ch[i];next.ch[i]=next.ch[7-i];next.ch[7-i]=tc; }
- son=cantor(next.ch); next.son=son;
- if(Node[son].father==-1)
- {
- Node[next.son].father=now.son; Node[next.son].way='A';
- Q.push(next);
- }
- next=now;
- tc=next.ch[3];for(i=3;i>0;i--) next.ch[i]=next.ch[i-1]; next.ch[0]=tc;
- tc=next.ch[4];for(i=4;i<7;i++) next.ch[i]=next.ch[i+1]; next.ch[7]=tc;
- son=cantor(next.ch); next.son=son;
- if(Node[son].father==-1)
- {
- Node[next.son].father=now.son; Node[next.son].way='B';
- Q.push(next);
- }
- next=now;
- tc=next.ch[5];next.ch[5]=next.ch[2];next.ch[2]=next.ch[1];next.ch[1]=next.ch[6];next.ch[6]=tc;
- son=cantor(next.ch); next.son=son;
- if(Node[son].father==-1)
- {
- Node[next.son].father=now.son; Node[next.son].way='C';
- Q.push(next);
- }
- }
- }
- int main()
- {
- int c,s,i;
- char str[9];
- char ch1[9]={'1','2','3','4','5','6','7','8'};
- for(i=0;i<40321;i++)
- Node[i].father=-1;
- BFS(ch1);
- char Way[10000];
- while(cin>>ch1>>str)
- {
- char pos[10];
- char des[8];
- for( i=0;i<8;i++)//转换
- pos[ch1[i]-'0']=i+1+'0';
- for( i=0;i<8;i++)
- des[i]=pos[str[i]-'0'];
- s=cantor(des);
- i=0;
- while(0!=s)//从目标到初太搜索路径
- {
- Way[i++]=Node[s].way;//printf("7 ");
- s=Node[s].father;
- }
- while(i--)//输出从初态到目标的路径
- {
- printf("%c",Way[i]);
- }
- printf("\n");
- }
- }
/*
63728145
86372541
ACBBBCBBCBCBCABB
下面是一步一步按顺序从队列中取300出来的:
12345678 87654321 41236785 17245368 58763214 82754631 34127856 48136275 86354271
41723685 16745238 65872143 51863724 13645728 58276314 83254761 23418567 3542718
6 57263184 34812756 47836125 58632714 24176853 48123765 41672385 76581432 645728
13 42736815 65187243 52163874 41367285 75823146 51876234 58327614 26318457 68172
453 23541867 38527416 65721843 13487562 35412876 34781256 35867142 51832674 7241
8536 25476183 56732184 24817653 46823175 74163852 48172635 73681542 31827546 764
58132 61472583 34278156 86512437 64587123 65218743 64132857 48167325 27581463 74
523816 43267815 75182346 53176824 25836147 51827364 75481362 12634578 25618347 7
6814532 42358671 26341587 23854167 26578431 64521783 81345627 16387452 67821453
13548762 37512486 83472561 35481726 63581427 34567812 47623815 35186742 57132864
73218456 38167452 72541836 28576413 35671842 12486537 25417863 24681753 6741852
3 75463182 53627184 74816352 43872165 24518637 87365421 74381652 23185467 576413
28 73658412 76145832 73421568 35478216 18654372 83612547 32178546 86451237 62487
513 16527438 64518273 36418572 65432187 52376184 64813257 42867135 26781543 6183
2547 27458163 71423586 64328157 87513462 74582136 75318246 32581476 24536817 463
72815 25183647 56127834 87543621 31265784 17234658 12563478 17685324 73614852 54
236718 47258361 78514362 42635871 28641357 52381674 26354817 72654318 23678541 3
8712546 26457831 68421573 82145367 25478361 81634527 15687342 26784531 41357628
16348572 13754862 78345612 86372451 62718453 83547261 62381547 21876543 63458127
31467582 24768153 83517426 34586172 35718642 65481237 17324568 63814527 7324158
6 72854136 73568421 34571682 81245376 13286457 36871452 12548637 26517483 824675
31 25481673 28136457 67541823 78563412 25361847 17483526 75416832 12456378 68734
215 82765341 87436521 82314675 26385147 45763281 52741638 21485637 57364128 7135
8642 47618325 73645182 27345681 76321458 61287453 73542168 31578426 17854632 745
21638 18365472 84312657 73215468 58642371 83651427 86245137 21654387 13627548 37
281546 16452738 37618452 78123456 36541872 68532417 75231846 16482573 65413827 6
4281357 34518762 82675431 36185472 26758413 27145863 26431578 65428317 18754623
86713542 63128547 87451362 73482516 17532468 74518326 71863542 32458176 21436587
74638152 82516473 24583167 48756213 82743561 63127845 38165274 85643271 3172658
4 15734268 61254783 17263548 81763245 12785634 25841637 17368524 75314682 514362
78 16385274 54723618 46758231 17853624 34268715 47235681 42863571 85236741 57281
364 71845362 52638174 71254638 14587632 72365418 24378651 13875462 52648317 2365
7481 26845731 76354128 48213675 72543618 82134657 81563427 82675314 23684751 541
36287 42157368 27584361 41635728 17648352 51378624 16354782 15427368