bzoj3757: 苹果树
传送门:http://www.lydsy.com:808/JudgeOnline/problem.php?id=3757
思路:像这种链剖 or lct没法做的就是树上莫队了...
不是树上的莫队就是按询问的左端点所在的块为第一关键字,右端点为第二关键字。
但是树上的就不同了,树上不是区间。
于是我们就进行树分块——见bzoj1086
注意这个分块是不需要保证每块的点都联通的,这个分块只要使莫队算法的复杂度有保证就可以了。
也就是块数是O(sqrt(n))的,块的大小是O(sqrt(n))的,块内两点的距离是O(sqrt(n)),相邻两块的距离是O(sqrt(n))的
这样莫队的暴力移复杂度才有保证
于是我们就可以以第一个节点所在块为第一关键字,第二个节点的dfs序为第二关键字对询问排序
然后我们考虑怎么由询问(curU,curV)得到询问(targetU,targetV)的答案
以下来自神犇vfk的博客(看的我整个人都不好了)
http://vfleaking.blog.163.com/blog/static/174807634201311011201627/
用S(v, u)代表 v到u的路径上的结点的集合。
用root来代表根结点,用lca(v, u)来代表v、u的最近公共祖先。
那么
S(v, u) = S(root, v) xor S(root, u) xor lca(v, u)
其中xor是集合的对称差。
简单来说就是
节点出现两次消掉。
lca很讨厌,于是再定义
T(v, u) = S(root, v) xor S(root, u)
观察将curV移动到targetV前后T(curV, curU)变化:
T(curV, curU) = S(root, curV) xor S(root, curU)
T(targetV, curU) = S(root, targetV) xor S(root, curU)
取对称差:
T(curV, curU) xor T(targetV, curU)= (S(root, curV) xor S(root, curU)) xor (S(root, targetV) xor S(root, curU))
由于对称差的交换律、结合律:
T(curV, curU) xor T(targetV, curU)= S(root, curV) xor S(root, targetV)
两边同时xor T(curV, curU):
T(targetV, curU)= T(curV, curU) xor S(root, curV) xor S(root, targetV)
发现最后两项很爽……哇哈哈
T(targetV, curU)= T(curV, curU) xor T(curV, targetV)
(有公式恐惧症的不要走啊 T_T)
也就是说,更新的时候,xor T(curV, targetV)就行了。
即,对curV到targetV路径(除开lca(curV, targetV))上的结点,将它们的存在性取反即可。
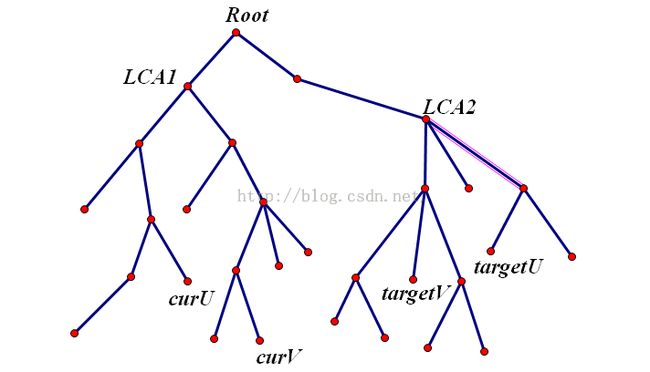
还是画图吧,假设有这样的一棵树和两组询问(画的好像有点丑...)
现在的答案是黄点的答案
而我们要求的是这些蓝点的答案
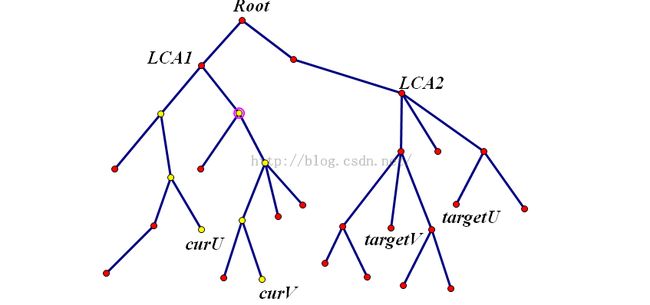
考虑怎么从黄点变成蓝点?
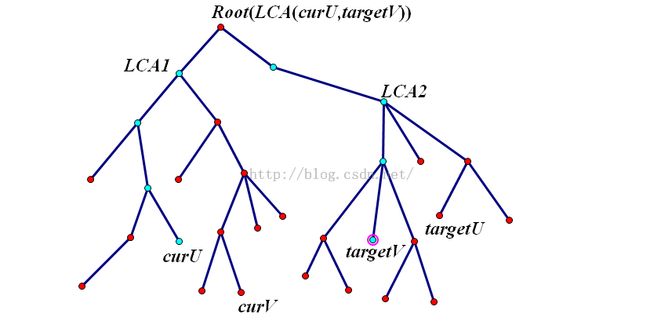
就是XOR上S(curV,root) xor S(curV,targetV),也就是对curV到targetV的路径上的点(除了lca)的存在性取反。
这样我们就可以先把LCA扔出去,算剩下部分的答案,再加上lca的贡献,然后就没有然后了。。。