叉积判断点在多边形内外 & poj2318
计算几何中长遇到的问题:判断特定点是否在平面多边形内部。向量叉积是一种方法,用于凸多边形。【优角:角度值大于180度小于360度。凸多边形:沿着多边形的一边做一条直线,如果剩下所有的部分都在直线的同侧,那么称这是一个凸多边形,凸多边形是没有优角的】
判断:连接第i条边的第一个端点和测试点成向量u,再连接第一个端点与第二个端点成向量v,记录叉积结果,除第一条边外,叉积结果和上一条边对应的叉积的乘积是正数的话继续判断,负数则不在多边形内。
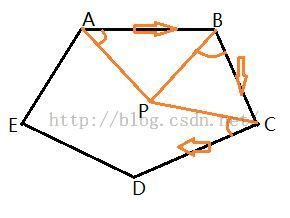
结果为正也就意味着点和边的时针方向是一致的,边按照一定的时针方向构成多边形。所有点都是如此的话点自然在多边形的内部。
struct Edge{
point p1,p2;
};
bool inside(point p,edge[],int n){ //n是多边形的边数
int now,pre;
for(int i=0;i<n;i++){
now=multi(p,edge[i].p1,edge[i].p2);
if(i>0&&now*pre<0) return 0;
pre=now;
}
return 1;
}
问题:http://poj.org/problem?id=2318

大意是寻找在如上的不同分区中有多少的点。
本题用两种做法:
1. 用叉积判断点在边的左右,加二分查找
我们已知一个事实:
用叉积函数计算
int cross(point p1,point p2,point p0){
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
得到的结果和两个向量的夹角的余弦值相关,如果它是正数就是逆时针方向,负数就是顺时针方向。(逆正顺负——前提是函数的参数不要弄错了)于是将题目中的edge两个端点作为p1,p2,根据正负就能判断点是在边的左右。正在左,负在右。
为加快查找速度,输入一个点就用二分找到对应的分区位置。叉积大于0则在边的左边,继续向左找,小于0在边的右边,继续向右找,直到low=high跳出循环,这时的high和low的变化要注意,不同于mid+1,mid-1。下面代码中的sum[i]的下标代表多边形的右边。
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=5e3+10;
struct point {
int x,y;
}; //point[maxn]
struct Edge{
point p1,p2;
}edge[maxn];
int sum[maxn];
int multi(point p1,point p2,point p0){
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
/*
常用二分是low=1,high=length,mid; low=mid+1; high=low-1;
这里low=1; high=length; mid; low=mid+1; high=mid;
*/
void midfind(point p,int n){ //直接判断在边的左侧还是右侧
int low=1,high=n,mid;
while(low<high){
mid=(low+high)/2;
if(multi(p,edge[mid].p2,edge[mid].p1)<0) low=mid+1;
else high=mid;
}
if(multi(edge[low].p1,edge[low].p2,p)<0) sum[low]++;
else sum[low+1]++;
}
int main()
{
//freopen("cin.txt","r",stdin);
int n,m,x1,x2,y1,y2,ca=0;
while(cin>>n&&n){
memset(sum,0,sizeof(sum));
if(ca)puts("");
ca++;
scanf("%d%d%d%d%d",&m,&x1,&y1,&x2,&y2);
int a,b;
for(int i=1;i<=n;i++){
scanf("%d%d",&a,&b);
edge[i].p1.x=a;
edge[i].p1.y=y1;
edge[i].p2.x=b;
edge[i].p2.y=y2;
}
for(int i=0;i<m;i++){
point p0;
scanf("%d%d",&p0.x,&p0.y);
midfind(p0,n);
}
for(int i=1;i<=n+1;i++){
printf("%d: %d\n",i-1,sum[i]);
}
}
return 0;
}
2. 用叉积计算多边形面积,直接遍历查找。
另一种思路相对简单,我们直接用叉积求面积,对于一个由左右两线段和上下平行线围成的梯形,如果面积相等就在多边形内部,大于原来的多边形面积就在外部。直接二重遍历即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
struct point{
int x,y;
};
struct edge{
point pl,pr;
}eg[5050];
int cnt,sum[5050];
int cmp(edge a,edge b){
int m1=min(a.pl.x,a.pr.x),q1=max(a.pl.x,a.pr.x);
int m2=min(b.pl.x,b.pr.x),q2=max(b.pl.x,b.pr.x);
return m1<m2||(m1==m2&&q1<q2);
}
int cross(point p1,point p2,point p0){
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
int myabs(int x){
return x<0?-x:x;
}
int main()
{
//freopen("cin.txt","r",stdin);
int n,m;
int x1,y1,x2,y2;
bool tag=0;
while(~scanf("%d",&n)&&n){
if(tag) puts("");
tag=1;
scanf("%d%d%d%d%d",&m,&x1,&y1,&x2,&y2);
int u,l;
cnt=0;
memset(sum,0,sizeof(sum));
for(int i=0;i<n;i++){
scanf("%d%d",&u,&l);
eg[cnt].pl.x=u; eg[cnt].pl.y=y1;
eg[cnt].pr.x=l; eg[cnt++].pr.y=y2;
}
eg[cnt].pl.x=x1; eg[cnt].pl.y=y1;
eg[cnt].pr.x=x1; eg[cnt++].pr.y=y2;
eg[cnt].pl.x=x2; eg[cnt].pl.y=y1;
eg[cnt].pr.x=x2; eg[cnt++].pr.y=y2;
sort(eg,eg+cnt,cmp);
for(int i=0;i<m;i++){
point p0;
scanf("%d%d",&p0.x,&p0.y);
for(int j=0;j<cnt-1;j++){
int d1=eg[j+1].pl.x-eg[j].pl.x;
int d2=eg[j+1].pr.x-eg[j].pr.x;
int s1=(d1+d2)*(y1-y2);
int s2=myabs(cross(eg[j].pl,eg[j].pr,p0))+myabs(cross(eg[j+1].pr,eg[j+1].pl,p0));
s2=s2+d1*(y1-p0.y)+d2*(p0.y-y2);
//if(p0.x==2&&p0.y==8) cout<<s1<<" "<<s2<<endl;
if(s1==s2){
sum[j]++;
break;
}
}
}
for(int i=0;i<=n;i++){
printf("%d: %d\n",i,sum[i]);
}
}
return 0;
}