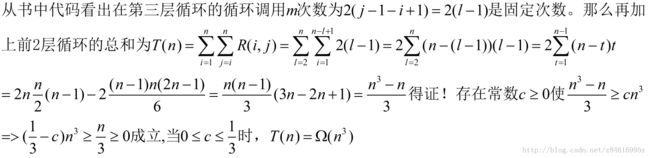算法导论第十五章动态规划
概述:
15.1钢条切割
钢条切割问题:给定定长的钢条和价格表,求切割方案,使得收益最大。如果n英寸的钢条的价格足够大,则不需要切割。
代码如下:
//朴素递归求解钢条切割收益,由于递归过程中反复求解同一个子问题,所以导致递归次数呈指数级增长,运行时间也过长。
#include <iostream>
using namespace std;
int Max(int a,int b)
{
return a>b?a:b;
}
int CUT_ROD(int p[],int n)
{
if (n==0)
{
return 0;
}
int q=-0x7fffffff;
for (int i=0;i<n;i++)
{
q=Max(q,p[i]+CUT_ROD(p,n-i-1));
}
return q;
}
void main()
{
const int n=10;
int p[n]={1,5,8,9,10,17,17,20,24,30};
cout<<CUT_ROD(p,4);
}
使用动态规划方法求解最优钢条切割问题
动态规划有两种等价实现方式:
① 带备忘的自顶向下法,用自然的递归方式,但是过程会保存每个子问题的解。节省了递归时间。
②自底向上法,需要恰当定义子问题“规模”,使其从小到大顺序求解。求解问题时,其子问题总是先解决了。
代码如下:
//下面在求解钢条切割过程中,可能重复求解的子问题都保存起来,使所有子问题仅求解一次,这样运行时间会变为多项式时间。
#if 0
#include <iostream>
using namespace std;
int Max(int a,int b)
{
return a>b?a:b;
}
int MEMOIZED_CUT_ROD_AUX(int p[],int n,int r[])
{
static int q;
if (r[n]>=0)
{//保存已求过的值。
return r[n];
}
if (n==0)
{
q=0;
}
else
{
q=-0x7fffffff;
for (int i=0;i<n;i++)
{
q=Max(q,p[i]+MEMOIZED_CUT_ROD_AUX(p,n-i-1,r));
}
}
r[n]=q;
return q;
}
int MEMOIZED_CUT_ROD(int p[],int n)
{//方法①自顶向下的动态规划方案
int *r=new int[n];
for (int i=0;i<n;i++)
{
r[i]=-0x7fffffff;
}
return MEMOIZED_CUT_ROD_AUX(p,n,r);
}
int BOTTOM_UP_CUT_ROD(int p[],int n)
{//方法②自底向下的动态规划方案
int *r=new int[n];
r[0]=0;
for (int j=0;j<n;j++)
{
int q=-0x7fffffff;
//int q=p[j+1];
for (int i=0;i<=j;i++)
{
q=Max(q,p[i]+r[j-i]);
}
r[j+1]=q;
}
return r[n];
}
void main()
{
const int n=10;
int p[10]={1,5,8,9,10,17,17,20,24,30};
cout<<MEMOIZED_CUT_ROD(p,9)<<endl;
cout<<BOTTOM_UP_CUT_ROD(p,9)<<endl;
}
子问题图
子问题图规模可以确定动态规划算法的运行时间。其运行时间与图的顶点和边的数量呈线性关系。
重构解:对于钢条切割方案,我们上文仅求最大收益,没有返回对应方案,所以下面代码是既返回收益,同时也返回方案。
//既返回收益,也返回最佳方案。
#include <iostream>
using namespace std;
struct array
{
int r;//代表最大收益
int s;//代表切割方案
};
struct array *EXTENDED_BOTTOM_UP_CUT_ROD(int p[],int n)
{
struct array *rs=new struct array[n];
rs[0].r=0;
int q;
for (int j=0;j<n;j++)
{
q=-0x7fffffff;
//int q=p[j+1];
for (int i=0;i<=j;i++)
{
if (q<p[i]+rs[j-i].r)
{
q=p[i]+rs[j-i].r;
rs[j+1].s=i+1;
}
}
rs[j+1].r=q;
}
return rs+n;
}
void PRINT_CUT_ROD_SOLUTION(int p[],int n)
{
struct array *rs=EXTENDED_BOTTOM_UP_CUT_ROD(p,n);
while (n>0)
{
cout<<(*rs).s<<" ";
n=n-(*rs).s;
rs=rs-(*rs).s;
}
}
void main()
{
const int n=10;
int p[10]={1,5,8,9,10,17,17,20,24,30};
cout<<(*EXTENDED_BOTTOM_UP_CUT_ROD(p,4)).r<<endl;
PRINT_CUT_ROD_SOLUTION(p,4);
}
练习:
15.1-1由公式(15.3)和初始条件T(0)=1,证明公式(15.4)成立。
T(n)=1+T(0)+T(1)+...T(n-1) 则有T(n-1)=1+T(0)+T(1)+....+T(n-2) 所以T(n)=2*T(n-1) ,所以根据这个递归式有:(T(1)/T(0))*(T(2)/T(1))........T(n)/T(n-1)=T(n)/T(0)=2^n 因为T(0)=1
所以T(n)=2^n成立。
15.1-2 举反例证明下面的“贪心”策略不能保证总是得到最优切割方案。定义长度为i的钢条的密度pi/i,即每英寸的价值。贪心策略将长度为n的钢条切割下长度为i(1<i<n)的一段,其密度最高。接下来继续使用相同的策略切割长度为n-i的剩余部分。
n=1 密度为1,n=2,密度为2.5 ,n=3 密度为2.7 n=4 密度为2.25 那么如果我们有一条4英寸的钢条,从密度最高处切割,那么就是从n=3处切割,收益为8,剩余的部分为n=1,收益为1,总收益为8+1=9. 但是如果从n=2处切割呢,两段都为2英寸,那么总收益就是5+5=10>9 但是这不是密度最高处。所以题目所给方案不能确定最大收益。
15.1-3 我们对钢条切割问题进行一点修改,除了切割下的钢条段具有不同价格pi外,每次切割还要付出固定的成本c.这样,切割方案的收益就等于钢条段价格之和减去切割的成本。设计一个动态规划算法解决修改后的钢条切割问题。
代码如下:此代码还记录的最优方案解
//15.1-3带有固定切割成本的钢条切割方案
#if 0
#include <iostream>
using namespace std;
int Max(int a,int b)
{
return a>b?a:b;
}
struct array
{
int r;//代表最大收益
int s;//代表切割方案
};
struct array *EXTENDED_BOTTOM_UP_CUT_ROD(int p[],int n)
{
struct array *rs=new struct array[n];
rs[0].r=0;
int q;
for (int j=0;j<n;j++)
{
int flag=1;//哨兵为1代表无切割。
q=p[j];
for (int i=0;i<j;i++)
{
//q=Max(q,p[i]+rs[j-i].r-1);
if(q<=p[i]+rs[j-i].r-1)//切割固定成本c=1
{
q=p[i]+rs[j-i].r-1;
rs[j+1].s=i+1;
flag=0;//哨兵为0代表有切割。
}
}
if (j==i)//i=j代表无切割
{
if (q<=p[i]+rs[j-i].r&&flag)
{//无切割时注意切割方案就等于钢条长度。
rs[j+1].s=i+1;
}
}
rs[j+1].r=q;
}
return rs+n;
}
void PRINT_CUT_ROD_SOLUTION(int p[],int n)
{
struct array *rs=EXTENDED_BOTTOM_UP_CUT_ROD(p,n);
while (n>0)
{
cout<<(*rs).s<<" ";
n=n-(*rs).s;
rs=rs-(*rs).s;
}
}
void main()
{
const int n=10;
int p[10]={1,5,8,9,10,17,17,20,24,30};
cout<<(*EXTENDED_BOTTOM_UP_CUT_ROD(p,10)).r<<endl;
PRINT_CUT_ROD_SOLUTION(p,10);
}
15.1-4 修改MEMOIZED-CUT-ROD,使之不仅返回最优收益值,还返回切割方案。
//15.1-4动态规划法递归求解最优钢条切割问题。不仅返回收益还返回切割方案。
#include <iostream>
using namespace std;
struct array
{
int r;//代表最大收益
int s;//代表切割方案
};
int Max(int a,int b)
{
return a>b?a:b;
}
struct array *MEMOIZED_CUT_ROD_AUX(int p[],int n,struct array rs[])
{
static int q;
if (rs[n].r>=0)
{
return rs+n;
}
if (n==0)
{
q=0;
}
else
{
q=-0x7fffffff;
for (int i=0;i<n;i++)
{
int t=p[i]+MEMOIZED_CUT_ROD_AUX(p,n-i-1,rs)->r;
if (q<t)
{
q=t;
rs[n].s=i+1;//n相当于上面迭代里的j+1,i+1和上面迭代一样。
}
}
}
rs[n].r=q;
return rs+n;
}
struct array *MEMOIZED_CUT_ROD(int p[],int n)
{
struct array *rs=new struct array [n];
for (int i=0;i<=n;i++)
{
rs[i].r=-0x7fffffff;
}
return MEMOIZED_CUT_ROD_AUX(p,n,rs);
}
void PRINT_CUT_ROD_SOLUTION(int p[],int n)
{
struct array *rs=MEMOIZED_CUT_ROD(p,n);
cout<<"最大收益:"<<rs->r<<endl;
cout<<"切割方案:";
while (n>0)
{
cout<<(*rs).s<<" ";
n=n-(*rs).s;
rs=rs-(*rs).s;
}
}
void main()
{
const int n=10;
int p[10]={1,5,8,9,10,17,17,20,24,30};
PRINT_CUT_ROD_SOLUTION(p,10);
cout<<endl;
}
15.1-5斐波那契额数列可以用递归式F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2).定义。设计一个O(n)时间的动态规划算法计算第n个斐波那契数。画出子问题图。图中有多少顶点和边?
代码如下:
#include <iostream>
using namespace std;
int f(int array[],int n)
{
if (n>=0)
{
array[0]=0;
}
if (n>=1)
{
array[1]=1;
}
for (int i=2;i<n;i++)
{
array[i]=array[i-1]+array[i-2];
}
return array[n];
}
子问题图:
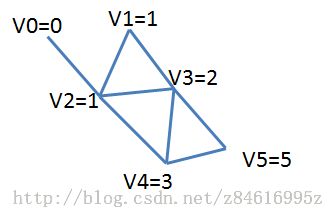 这是n=5是的子问题图,可以看出有6个顶点和8条边,推广到n情况,有n+1个顶点,有2n-2条边。
这是n=5是的子问题图,可以看出有6个顶点和8条边,推广到n情况,有n+1个顶点,有2n-2条边。
15.2矩阵链乘法
矩阵乘法的必要条件:矩阵A与B必须是相容的,即A的列数等于B的行数。
矩阵链乘法定义:一组矩阵相乘,求完全括号化方案,利用上一节讲的动态规划四个步骤即可计算出一组矩阵最少的相乘次数。
代码如下:
#include <iostream>
using namespace std;
#define n 5//可以更改矩阵的数量
struct Matrix
{
int rows;//表示行数。
int columns;//表示列数。
int **M;
Matrix(int i=0,int j=0)
{
rows=i;
columns=j;
M=new int *[rows];
for (int k=0;k<rows;k++)
{
M[k]=new int [columns];
}
};
};
struct Matrix_CHAIN//矩阵链
{
int **m;//运算次数
int **s;//划分方式
Matrix_CHAIN()
{
m=new int *[n-1];
for (int k=0;k<n-1;k++)
{
m[k]=new int [n-1];
}
s=new int *[n-2];
for (int t=0;t<n-1;t++)
{
s[t]=new int [n-1];
}
}
};
struct Matrix init(struct Matrix A)
{
for (int i=0;i<A.rows;i++)
{
for (int j=0;j<A.columns;j++)
{
A.M[i][j]=rand()%10;
}
}
return A;
}
struct Matrix Matrix_MULTIPLY(struct Matrix A,struct Matrix B)
{
if (A.columns!=B.rows)
{
struct Matrix D(1,1);
D.M[0][0]=0;
cerr<<"incompatible dimensions"<<endl;
return D;
}
else
{
struct Matrix C(A.rows,B.columns);
for (int i=0;i<A.rows;i++)
{
for (int j=0;j<B.columns;j++)
{
C.M[i][j]=0;
for (int k=0;k<A.columns;k++)
{
C.M[i][j]=C.M[i][j]+A.M[i][k]*B.M[k][j];
}
}
}
return C;
}
}
struct Matrix_CHAIN MATRIX_CHAIN_ORDER(int p[])
{
int N=n-1;
Matrix_CHAIN T;
for (int i=0;i<N;i++)
{
T.m[i][i]=0;
}
for (int l=2;l<=N;l++)
{
for (int i=1;i<=N-l+1;i++)
{
int j=i+l-1;
T.m[i-1][j-1]=0x7fffffff;
for (int k=i;k<=j-1;k++)
{
int q=T.m[i-1][k-1]+T.m[k][j-1]+p[i-1]*p[k]*p[j];
if (q<T.m[i-1][j-1])
{
T.m[i-1][j-1]=q;
T.s[i-1][j-1]=k-1;
}
}
}
}
return T;
}
//15.2-2矩阵链总乘法
struct Matrix MATRIX_CHAIN_MULTIPLY(Matrix A[],Matrix_CHAIN T,int i,int j)
{
if (j==i)
{
return A[i];
}
if (j==i+1)
{
return Matrix_MULTIPLY(A[i],A[j]);
}
Matrix t1=MATRIX_CHAIN_MULTIPLY(A,T,i,T.s[i][j]);
Matrix t2=MATRIX_CHAIN_MULTIPLY(A,T,T.s[i][j]+1,j);
return Matrix_MULTIPLY(t1,t2);
}
void PRINT_OPTIMAL_PARENS(Matrix_CHAIN T,int i,int j)
{
if (i==j)
{
cout<<"A"<<i;
}
else
{
cout<<"(";
PRINT_OPTIMAL_PARENS(T,i,T.s[i][j]);
PRINT_OPTIMAL_PARENS(T,T.s[i][j]+1,j);
cout<<")";
}
}
void Print(struct Matrix A)
{
for (int i=0;i<A.rows;i++)
{
for (int j=0;j<A.columns;j++)
{
cout<<A.M[i][j]<<" ";
}
cout<<endl;
}
}
void main()
{
//int p[n]={5,10,3,12,5,50,6};
//int p[n]={30,35,15,5,10,20,25};
int p[n]={2,3,4,5,6};
struct Matrix_CHAIN T=MATRIX_CHAIN_ORDER(p);
for (int i=0;i<n-1;i++)
{
for (int j=0;j<n-1;j++)
{
if (T.m[i][j]<0)
{
cout<<"-1"<<"\t";
}
else cout<<T.m[i][j]<<"\t";
}
cout<<endl;
}
PRINT_OPTIMAL_PARENS(T,0,n-2);
struct Matrix A[n]={0};
for (int j=1;j<n;j++)
{
struct Matrix t(p[j-1],p[j]);
A[j-1]=t;
init(A[j-1]);
cout<<endl;
Print(A[j-1]);
cout<<endl;
}
struct Matrix C=MATRIX_CHAIN_MULTIPLY(A,T,0,n-2);
Print(C);
}
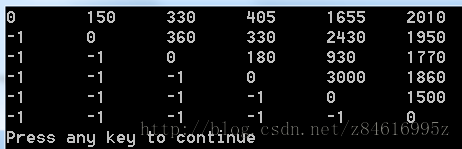
15.2-1 对矩阵规模序列{5,10,3,12,5,50,6},求矩阵链最优括号化方案。
利用上面代码:得到下图所示结果:
15.2-2设计递归算法MATRIX-CHAIN-MULTIPLY(A,s,i,j),实现矩阵链最优代价乘法计算的真正计算过程,其输入参数为矩阵序列{A1,A2,...,An},MATRIX-CHAIN-ORDER得到的表s,以及下标i和j.(初始调用应为MATRIX-CHAIN-MULTIPLY(A,s,1,n)).
由于数组下标是从0开始的,所以 这里调用应为MATRIX-CHAIN-MULTIPLY(A,s,0,n-2)).n为矩阵链元素个数,上面代码中的n为矩阵链长度,实际矩阵个数N=n-1个。
15.2-3 用代入法证明递归公式(15.6)的结果为Ω(2^n).
P(n-1)=P(1)P(n-2)+P(2)P(n-3)+....+P(n-2)P(1) P(n)=P(1)P(n-1)+P(2)P(n-2)+....+P(n-1)P(1) 因为P(1)<P(2)<...P(n-1) 所以P(n)>P(1)P(n-1)+P(n-1) 因为P(1)=1 P(n)>2P(n-1)
猜想P(n)>c2^n,则P(n-1)>c2^(n-1) 所以P(n)>2c2^(n-1)=c2^n 得证!
15.2-4 对输入链长度为n的矩阵连乘法问题,描述其子问题图:它包含多少个顶点?包含多少条边?这些分别连接哪些顶点?
包含n²个顶点,n³条边连接着n²个顶点。
15.2-5 令R(i,j)表示在一次调用MATRIX-CHAIN-ORDER过程中,计算其他表项时访问表项m[i,j]的次数。证明:(提示:证明中可用到公式A.3)
15.2-6 证明:对n个元素的表达式进行完全括号化,恰好需要n-1对括号。
利用归纳法即可证明。当n≤2时 恰好有1对括号。假设当n=k(2<k<n)时,有k-1对括号。则n=k+1时,现在我们把这k+1个矩阵分成k个矩阵+1个矩阵,前k个矩阵在前面假设中已知只要加k-1对括号就可以使最终结果是最优的,那么保持前k个矩阵的括号划分,并且得到最优结果矩阵后,再与第k+1个矩阵相乘,这时问题又转化为2个矩阵相乘的简单问题了,由前面已知需要1对括号,那么总的括号就是k-1+1=k对括号,在n=k+1时,也成立。所以利用归纳法得证!
15.3动态规划原理
15.3-1对于矩阵链乘法问题,下面两种确定最优代价的方法哪种更高效?第一种方法是穷举所有可能的括号化方案,对每种方案计算乘法运算次数,第二种方法是运行RECURSIVE-MATRIX-CHAIN。证明你的结论。
书中对枚举法已经给出其运行时间,就是类似卡塔兰数的序列,运算次数为Ω(4^n/n^(3/2))。而用朴素递归方式求全部解的运算次数为O(n3^n).显然用递归方式求解更高效。
15.3-2 对一个16个元素的数组,画出2,.3-1节中MERGE-SORT过程运行的递归调用树。解释备忘技术为什么对MERGE-SORT这种分治算法无效。
参考书中图2-4,这里只是把原书8个元素扩展到16个元素,两者类似。由2-4图可以看出,每个子问题都是全新的,不存在重叠子问题,所以图中问题适合分治而不适合动态规划。
15.3-3 考虑矩阵链乘法问题的一个变形,目标改为最大化矩阵序列括号花方案的变量乘法运算次数,而非最小化。此问题具有最优子结构性质吗?
由于矩阵链中的子问题链为AiAi+1...Ak和Ak+1Ak+2....Aj的乘法问题,子链是互不相交的,因此任何矩阵都不会同时包含在两个子链中。这样我们说矩阵链子问题是无关的。于是我们可以用“剪切-黏贴”技术来加以证明这个事具有最优子结构的。
15.3-4 如前所述,使用动态规划方法,我们首先求解子问题,然后选择哪些子问题用来构造原问题的最优解。Capulet教授认为,我们不必为了求原问题的最优解而总是求解出所有子问题。她建议,在求矩阵链乘法问题的最优解时,我们总是可以在求解子问题之前选定AiAi+1...Aj的划分位置Ak(选定的k使得pi-1pkpj最小)。请找出一个反例,证明这个贪心方法可能生成次优解。
代码片段如下:
struct Matrix_CHAIN MATRIX_CHAIN_ORDER(int p[])
{
int N=n-1;
Matrix_CHAIN T;
for (int i=0;i<N;i++)
{
T.m[i][i]=0;
}
for (int l=2;l<=N;l++)
{
for (int i=1;i<=N-l+1;i++)
{
int j=i+l-1;
T.m[i-1][j-1]=0x7fffffff;
int q1=0x7fffffff;
for (int k=i;k<=j-1;k++)
{
int q=T.m[i-1][k-1]+T.m[k][j-1]+p[i-1]*p[k]*p[j];
#if 0//0表示不执行此if语句。
if (q<T.m[i-1][j-1])
{//正常的划分。用于和下面做对比。
T.m[i-1][j-1]=q;
T.s[i-1][j-1]=k-1;
}
#endif
#if 1//1表示执行此if语句。
if (q1>p[i-1]*p[k]*p[j])
{//选定k使pi-1pkpj最小=Capulet教授方法
T.m[i-1][j-1]=q;
q1=p[i-1]*p[k]*p[j];
T.s[i-1][j-1]=k-1;
}
#endif
}
}
}
return T;
}
代码结果对比图:
 代码数据为int p[4]={5,10,20,25};
代码数据为int p[4]={5,10,20,25};
15.3-5 对15.1节的钢条切割问题加入限制条件:假定对于每种钢条长度i(i=1,2,...n-1),最多允许切割出li段长度为i的钢条。证明:15.1节所描述的最优子结构性质不再成立。
 从图中看出如果切割1个长度为4的钢条,最佳切割方式是切成4条长度为1的钢条可以获得60最大收益,但是我们给每种长度对应的价格做了限制,比如长度为1的钢条最多只能切割2段,那么4>2超出预期。所以我们在不违反切割限制前提下只能选择切成长度分别为1,1和2的钢条作为最佳切割方式,收益为50。由于加了切割限制,所以最优子结构性质不再成立。
从图中看出如果切割1个长度为4的钢条,最佳切割方式是切成4条长度为1的钢条可以获得60最大收益,但是我们给每种长度对应的价格做了限制,比如长度为1的钢条最多只能切割2段,那么4>2超出预期。所以我们在不违反切割限制前提下只能选择切成长度分别为1,1和2的钢条作为最佳切割方式,收益为50。由于加了切割限制,所以最优子结构性质不再成立。
#if 1//书中所给代码
#include <iostream>
#include <string>
using namespace std;
#define M 6
#define N 7
char *b[N+1][M+1]={NULL};
int c[N+1][M+1]={0};
void Lcs_Length(char *x, char *y)
{
for (int i1=0;i1<=N;i1++)
{
b[i1][0]="NULL";
}
for (int j1=0;j1<=M;j1++)
{
b[0][j1]="NULL";
}
for (int i=1;i<=N;i++)
{
for (int j=1;j<=M;j++)
{
if (x[i]==y[j])
{
c[i][j]=c[i-1][j-1]+1;
b[i][j]="↖";
}
else
{
if (c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];
b[i][j]="↑";
}
else
{
c[i][j]=c[i][j-1];
b[i][j]="←";
}
}
}
}
}
void PRINT_LCS(char*x,int i,int j)
{
if (i==0||j==0)
{
return;
}
if (b[i][j]=="↖")
{
PRINT_LCS(x,i-1,j-1);
cout<<x[i]<<" ";
}
else
{
if (b[i][j]=="↑")
{
PRINT_LCS(x,i-1,j);
}
else
{
PRINT_LCS(x,i,j-1);
}
}
}
void main()
{
char x[N+1] = {'\0','A','B','C','B','D','A','B'};
char y[M+1] = {'\0','B','D','C','A','B','A'};
//char x[M+1] = {'1','0','0','1','0','1','0','1'};
//char y[N+1] = {'0','1','0','1','1','0','1','1','0'};
Lcs_Length(x, y);
PRINT_LCS(x,N,M);
cout<<"书中图15-8中的表格:"<<endl;
for (int i=0;i<=N;i++)
{
for (int j=0;j<=M;j++)
{
cout<<b[i][j]<<"\t";
}
cout<<endl;
for (j=0;j<=M;j++)
{
cout<<c[i][j]<<"\t";
}
cout<<endl;
}
}
#endif
#include <iostream>
using namespace std;
#define M 6
#define N 7
void Lcs_Length(char *x, char *y,int c[][M+1])
{
for (int i=1;i<=N;i++)
{
for (int j=1;j<=M;j++)
{
if (x[i]==y[j])
{
c[i][j]=c[i-1][j-1]+1;
}
else
{
if (c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];
}
else
{
c[i][j]=c[i][j-1];
}
}
}
}
}
void PRINT_LCS(int c[][M+1],char*x,int i,int j)
{
if (i==0||j==0)
{
return;
}
if (c[i][j]==c[i-1][j-1]+1)
{
PRINT_LCS(c,x,i-1,j-1);
cout<<x[i]<<" ";
}
else
{
if (c[i-1][j]>=c[i][j-1])
{
PRINT_LCS(c,x,i-1,j);
}
else
{
PRINT_LCS(c,x,i-1,j);
}
}
}
void main()
{
char x[N+1] = {'\0','A','B','C','B','D','A','B'};
char y[M+1] = {'\0','B','D','C','A','B','A'};
int c[N+1][M+1]={0};
Lcs_Length(x, y,c);
PRINT_LCS(c,x,N,M);
}
#include <iostream>
using namespace std;
#define M 6
#define N 7
int Max(int a,int b)
{
return a>b?a:b;
}
int Lcs_Length(char *x, char *y,int c[][M+1],int i,int j)
{
if (i==0||j==0)
{
c[i][j]=0;
}
else if (c[i][j]>0)
{
return c[i][j];
}
else
{
if (x[i]==y[j])
{
c[i][j]=Lcs_Length(x,y,c,i-1,j-1)+1;
}
else
{
c[i][j]=Max(Lcs_Length(x,y,c,i,j-1),Lcs_Length(x,y,c,i-1,j));
}
}
return c[i][j];
}
void main()
{
char x[N+1] = {'\0','A','B','C','B','D','A','B'};
char y[M+1] = {'\0','B','D','C','A','B','A'};
int c[N+1][M+1]={0};
cout<<Lcs_Length(x, y,c,N,M);
}
//15.4-4使用2*min(m,n)及O(1)的额外空间来计算LCS的长度(仅限于计算LCS长度而不关心LCS具体值)
#if 1
#include <iostream>
using namespace std;
#define M 6
#define N 7
#if 0//方法一(1) 存储2Xmin(m,n)表项+O(1)额外存储空间(自己写的,感觉用位操作比复制更快一些)
/*基本思想是用一个仅有2行的二维数组存储LCS长度,然后经过不断的异或二维数组的行数,当前行和
上一行之间不断的变换,最终把所有LCS长度数据存储好然后输入其值****************************/
void Lcs_Length4(char *x, char *y)
{
int t=0;
static int c2[2][M+1] = {0}; //c2是2*min(M,N)的矩阵,初始化
for(int i = 1; i <=N;i++,t^=1)
{ //t和1进行一次异或,t的值或由1变为0,或由0变为1.
for(int j = 1; j <=M; j++)
{
if(x[i]==y[j])
{
c2[t][j] = c2[t^1][j-1] + 1;
}
else
{
if(c2[t^1][j] >= c2[t][j-1])
{
c2[t][j] = c2[t^1][j];
}
else
{
c2[t][j] = c2[t][j-1];
}
}
}
}
int Max=c2[0][M-1]>c2[1][M-1]?c2[0][M-1]:c2[1][M-1];
cout<<Max<<endl; //输出结果
}
#endif
#if 1//方法一(2) 存储2Xmin(m,n)表项+O(1)额外存储空间(根据参考书上所给这种方法的思想写的代码)
/*基本思想也是用仅有2行的二维数组,用第0行作为上一行,第1行作为当前行,一次循环后,把旧的第1
行(当前行)的所有数据转移给新的上一行,而新的当前行用来存储新的当前行数据,这样不断循环,最终
得到LCS长度********************************************************************************/
void copy( int c2[][M+1])
{
for (int i=0;i<=M;i++)
{
c2[0][i]=c2[1][i];
}
}
void Lcs_Length4(char *x, char *y)
{
static int c2[2][M+1] = {0}; //c2是2*min(M,N)的矩阵,初始化
for(int i = 1; i <=N;i++)
{ //t和1进行一次异或,t的值或由1变为0,或由0变为1.
for(int j = 1; j <=M; j++)
{
if(x[i]==y[j])
{
c2[1][j] = c2[0][j-1] + 1;
}
else
{
if(c2[0][j] >= c2[1][j-1])
{
c2[1][j] = c2[0][j];
}
else
{
c2[1][j] = c2[1][j-1];
}
}
}
copy(c2);//复制当前行作为新的上一行。
}
cout<<c2[1][M-1]<<endl; //输出结果
}
#endif
#if 0 //方法二 存储min(m,n)表项+O(1)额外存储空间(根据参考书上所给这种方法的思想写的代码)
/*总的思想就是把数组a的第一个位置用来储存内层循环上一次循环的当前元素值用来更新当前元
素的前一个元素,然后再把本次循环的当前元素值更新a[0],把内层循环最后一个位置用a[0]填充
后,完成内层循环,然后进行外层循环,这样往复,直到把所有元素放入到正确位置上********/
void copy( int c2[][M+1])
{
for (int i=0;i<=M;i++)
{
c2[0][i]=c2[1][i];
}
}
void Lcs_Length4(char *x, char *y)
{
int a[M+1]={0};
int q=0;//q用来保存c[i,j]
for (int i=1;i<=N;i++)
{
for (int j=1;j<=M;j++)
{
if (x[i]==y[j])
{
q=a[j-1]+1;//a[j-1]=c[i-1,j-1]
}
else
{
if (a[j]>=a[0])//a[0]=c[i,j-1] a[j]=c[i-1,j]
{//当前元素的同列的上一行大于当前元素的同行的前一个元素
q=a[j];//上面两者谁大把它的值给当前元素
}
else
{
q=a[0];
}
}
a[j-1]=a[0];//a[0]的值是用来更新当前j的前一个元素
a[0]=q;//当前元素q=c[i,j]的值固定用来更新a[0]
}
a[M]=q;//内层循环完后,当前元素更新数组a的最后一个值
a[0]=0;//由于当前元素已经把本层循环最后一个元素填充满了,所以必须清0了。
}
cout<<a[M-1]<<endl;
}
#endif
int main()
{
char x[N+1] = {'\0','A','B','C','B','D','A','B'};
char y[M+1] = {'\0','B','D','C','A','B','A'};
//char x[M+1] = {'1','0','0','1','0','1','0','1'};
//char y[N+1] = {'0','1','0','1','1','0','1','1','0'};
Lcs_Length4(x, y);
return 0;
}
15.4-5-15.4-6
15.5-1 设计代码CONSTRUCT-OPTIMAL-BST(root),输入为表root,输出是最优二叉搜索树的结构。
#include <iostream>
using namespace std;
#define n 5
struct e_root//为了同时返回e和root,我们需要一个结构体
{
double **e;
int **root;
e_root()
{
e=new double *[n+2];
for (int i=0;i<n+2;i++)
{
e[i]=new double[n+1];
}
root=new int *[n+1];
for (int j=0;j<n+1;j++)
{
root[j]=new int[n+1];
}
};
};
struct e_root OPTIMAL_BST(double p[],double q[])
{
struct e_root T;
double w[n+2][n+1]={0};
for (int i=1;i<=n+1;i++)
{
T.e[i][i-1]=q[i-1];
w[i][i-1]=q[i-1];
}
for (int l=1;l<=n;l++)
{
for (int i=1;i<=n-l+1;i++)
{
int j=i+l-1;
T.e[i][j]=0x7fffffff;
w[i][j]=w[i][j-1]+p[j]+q[j];
for (int r=i;r<=j;r++)
{
double t=T.e[i][r-1]+T.e[r+1][j]+w[i][j];
if (t<T.e[i][j])
{
T.e[i][j]=t;
T.root[i][j]=r;
}
}
}
}
return T;
}
void PRINT_OPTIMAL_BST(struct e_root T,int i,int j)
{
int Root=T.root[i][j];//当前根结点
if (i==1&&j==n)
{
cout<<"k"<<Root<<"为根"<<endl;
}
if (i==Root)
{//如果左子树是叶子
cout<<"d"<<i-1<<"为k"<<Root<<"的左子树"<<endl;
}
else
{
cout<<"k"<<T.root[i][Root-1]<<"为k"<<Root<<"的左子树"<<endl;
PRINT_OPTIMAL_BST(T,i,Root-1);
}
if (j==Root)
{//如果右子树是叶子
cout<<"d"<<j<<"为k"<<Root<<"的右子树"<<endl;
}
else
{
cout<<"k"<<T.root[Root+1][j]<<"为k"<<Root<<"的右子树"<<endl;
PRINT_OPTIMAL_BST(T,Root+1,j);
}
}
void main()
{
double p[n+1]={0,0.15,0.10,0.05,0.10,0.20};//注意数组p的第一个位置不放任何数据。
double q[n+2]={0.05,0.10,0.05,0.05,0.05,0.10};
//double p[n+1]={0,0.04,0.06,0.08,0.02,0.10,0.12,0.14};//15.5-2题数据
// double q[n+2]={0.06,0.06,0.06,0.06,0.05,0.05,0.05,0.05};
struct e_root T=OPTIMAL_BST(p,q);
cout<<"最优二叉搜索树结构:"<<endl;
PRINT_OPTIMAL_BST(T,1,n);
cout<<"最优二叉搜索树代价:"<<T.e[1][n]<<endl;
}
#include <iostream>
using namespace std;
#define n 5
struct e_root//为了同时返回e和root,我们将这其放入结构体中。
{
double **e;
int **root;
e_root()
{
e=new double *[n+2];
for (int i=0;i<n+2;i++)
{
e[i]=new double[n+1];
}
root=new int *[n+1];
for (int j=0;j<n+1;j++)
{
root[j]=new int[n+1];
}
};
};
struct e_root OPTIMAL_BST(double p[],double q[])
{
struct e_root T;
double w[n+2][n+1]={0};
for (int i=1;i<=n+1;i++)
{
T.e[i][i-1]=q[i-1];
w[i][i-1]=q[i-1];
}
for (int l=1;l<=n;l++)
{
for (int i=1;i<=n-l+1;i++)
{
int j=i+l-1;
T.e[i][j]=0x7fffffff;
w[i][j]=w[i][j-1]+p[j]+q[j];
if (i==j)//当最优二叉搜索子树只有一个元素时
{
T.root[i][j]=j;
T.e[i][j]=T.e[i][j-1]+T.e[j+1][j]+w[i][j];
}
else//不止一个元素时
{//我们不用从i起一直检查到j,只需检查区间T.root[i][j-1]到T.root[i+1][j](根据题目给的不等式)
for (int r=T.root[i][j-1];r<=T.root[i+1][j];r++)
{
double t=T.e[i][r-1]+T.e[r+1][j]+w[i][j];
if (t<T.e[i][j])
{
T.e[i][j]=t;
T.root[i][j]=r;
}
}
}
}
}
return T;
}
void PRINT_OPTIMAL_BST(struct e_root T,int i,int j)
{
int Root=T.root[i][j];//当前根结点
if (i==1&&j==n)
{
cout<<"k"<<Root<<"为根"<<endl;
}
if (i==Root)
{//如果左子树是叶子
cout<<"d"<<i-1<<"为k"<<Root<<"的左子树"<<endl;
}
else
{
cout<<"k"<<T.root[i][Root-1]<<"为k"<<Root<<"的左子树"<<endl;
PRINT_OPTIMAL_BST(T,i,Root-1);
}
if (j==Root)
{//如果右子树是叶子
cout<<"d"<<j<<"为k"<<Root<<"的右子树"<<endl;
}
else
{
cout<<"k"<<T.root[Root+1][j]<<"为k"<<Root<<"的右子树"<<endl;
PRINT_OPTIMAL_BST(T,Root+1,j);
}
}
void main()
{
double p[n+1]={0,0.15,0.10,0.05,0.10,0.20};//注意数组p的第一个位置不放任何数据。
double q[n+2]={0.05,0.10,0.05,0.05,0.05,0.10};
//double p[n+1]={0,0.04,0.06,0.08,0.02,0.10,0.12,0.14};//15.5-2题数据
//double q[n+2]={0.06,0.06,0.06,0.06,0.05,0.05,0.05,0.05};
struct e_root T=OPTIMAL_BST(p,q);
cout<<"最优二叉搜索树结构:"<<endl;
PRINT_OPTIMAL_BST(T,1,n);
cout<<"最优二叉搜索树代价:"<<T.e[1][n]<<endl;
}