Neural Turing Machines-NTM系列（一）简述

Neural Turing Machines-NTM系列（一）简述

NTM是一种使用Neural Network为基础来实现传统图灵机的理论计算模型。利用该模型，可以通过训练的方式让系统“学会”具有时序关联的任务流。
论文：http://arxiv.org/abs/1410.5401
中文翻译：http://www.dengfanxin.cn/?p=60
ppt:http://llcao.net/cu-deeplearning15/presentation/NeuralTuringMachines.pdf
基于Theano的python语言实现1：https://github.com/shawntan/neural-turing-machines
基于Theano的python语言实现2：https://github.com/snipsco/ntm-lasagne
基于Torch的实现：https://github.com/kaishengtai/torch-ntm
基于Tensor Flow的实现：https://github.com/carpedm20/NTM-tensorflow
基于C#的实现：https://github.com/JanTkacik/NTM
基于JS语言的实现：https://github.com/gcgibson/NTM
GO语言实现：https://github.com/fumin/ntm
相关博客1：https://blog.wtf.sg/category/neural-turing-machines/
相关博客2 ：https://medium.com/snips-ai/ntm-lasagne-a-library-for-neural-turing-machines-in-lasagne-2cdce6837315#.twrvqnda9
百度贴吧：http://tieba.baidu.com/p/3404779569
知乎中关于强人工智能的一些介绍：http://www.zhihu.com/question/34393952

1.图灵机

首先，我们来复习一下大学的知识，什么是图灵机呢？图灵机并不是一个实体的计算机，而是一个理论的计算模型，由计算机技术先驱Turing在1936年提出（百度知道)
它包含如下基本元素：
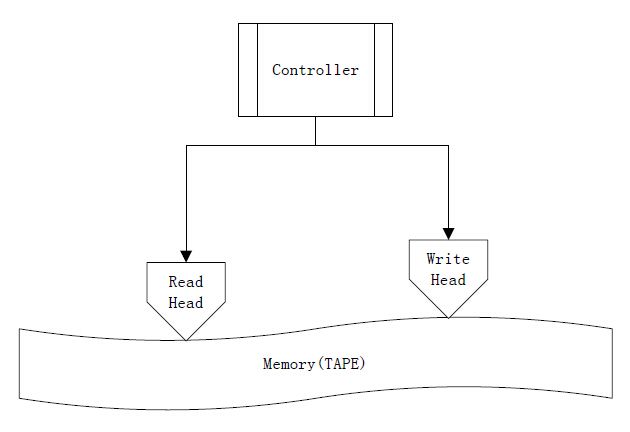
TAPE：磁带，即记忆体（Memory）
HEAD：读写头，read or write TAPE上的内容
TABLE：一套控制规则，也叫控制器（Controller），根据机器当前状态和HEAD当前所读取的内容来决定下一步的操作。在NTM中，TABLE其实模拟了大脑的工作记忆
register：状态寄存器，存储机器当前的状态。
如下图：

2. 神经图灵机（NTM）

所谓的NTM，其实就是使用NN来实现图灵机计算模型中的读写操作。其模型中的组件与图灵机相同。那么，NTM中是怎么实现的呢？

2.1 Reading 操作

假设t时刻的内存数据为 Mt , Mt 为一矩阵，大小为 N×M ，其中N为内存地址的数目，M为每个内存地址向量的长度。设 wt 为t时刻加于N个内存地址上的权值， wt 为一N维向量，且每个分量 wt(i) 满足：
∑iwt(i)=1,且∀i,0≤wt(i)≤1
定义读取向量为 rt （即t时刻Read Head读取出来的内容），大小为M，且满足：
rt=∑iwt(i)Mt(i)
显然， rt 是 Mt(i) 的凸组合。

2.2 Writing 操作

写操作分解为顺序执行的两步：
1.擦除（erase）
2.添加（add）
wt 为Write Head发出的权值向量， et 为擦除向量，它们的所有分量值都在0,1之间，前一个时刻的Memory修改量为:
M˜t(i)=Mt−1(i)∘[1−wt(i)et]
式中的空心圆圈表示向量按元素逐个相乘（point-wise）,显然，这里的 et 指出了每个分量将被擦除的量。举个简单的例子：
假设 N=2,M=3
Mt−1=(142536)
wt=[0.1,0.3,0.7]T
et=[0.2,0.5,0.6]
M˜t(1)=Mt−1(1)∘[1−wt(1)et]
=[1,2,3]∘(1−0.1∗[0.2,0.5,0.6])=[1,2,3]∘[0.98,0.95,0.94]=[0.98,1.9,1.88]

如果不考虑 wt 的影响，我们可以简单的认为 et 的值代表将擦除的量，比如上例中的[0.2,0.5,0.6]，可以认为内存中每个分量将分别被擦去原值的0.2,0.5,0.6，而 wt 相当于每个分量将要被修改的权重。
如果要完全擦除一个分量，只需要对应的 wt(i) 和 et 都为1。当 et 为0时，将不进行任何修改。
Write Head还需要生成一个长度为 M 的 add 向量 at ，在 erase 操作执行完之后，它将被“加”到对应的内存地址中。
t时刻的内存值将为：
Mt(i)=M˜t(i)+wt(i)at
显然， erase 和 add 操作都是可微的，它们的组合操作writing也同样是可微的，writing可以对任意地址的元素值进行任意精度的修改。

3.NTM的寻址策略

有两种寻址策略，

3.1 Content-base(基于内容的寻址)：

产生一个待查询的值 kt ，将该与 Mt 中的所有 N 个地址的值进行比较，最相近的那个 Mt(i) 即为待查询的值。
首先，需要进行寻址操作的Head(Read or Write)生成一个长度为M的key vector: kt ,然后将 kt 与每个 Mt(i) 进行相似度比较（相似度计算函数为 K[u,v] ），最后将生成一个归一化的权重向量 wct ,计算公式如下：
wct(i)=eβtK[kt,Mt(i)]∑jeβtK[kt,Mt(j)]
其中， βt满足βt>0 是一个调节因子，用以调节寻址焦点的范围。 βt 越大，函数的曲线变得越发陡峭，焦点的范围也就越小。
相似度函数这里取余弦相似度： K[u,v]=u⋅v||u||⋅||v||

3.2 Location-base(基于位置的寻址)：

直接使用内存地址进行寻址，跟传统的计算机系统类似，controller给出要访问的内存地址，Head直接定位到该地址所对应的内存位置。对于一些对内容不敏感的操作，比如乘法函数 f(x,y)=xy ，显然该操作并不局限于x，y的具体值，x,y的值是易变的，重要的是能够从指定的地址中把它们读出来。这类问题更适合采用Location-base的寻址方式。
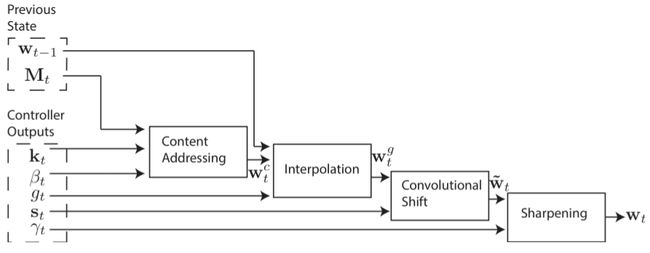
基于地址的寻址方式可以同时提升简单顺序访问和随机地址访问的效率。我们通过对移位权值进行旋转操作来实现优化。例如，当前权值聚焦在一个位置，旋转操作1将把焦点移向下一个位置，而一个负的旋转操作将会把焦点移向上一个位置。
在旋转操作之前，将进行一个插入修改的操作(interpolation),每个head将会输出一个修改因子 gt且gt∈[0,1] ，该值用来混合上一个时刻的 wt−1 和当前时刻由内容寻址模块产生的 wct ，最后产生门限权值 wgt :
wgt=gtwct+(1−gt)wt−1
显然， gt 的大小决定了 wct 所占的分量， gt 越大，系统就越倾向于使用Content-base Addressing。当 gt=1 时，将完全按照Content-base方式进行寻址。
在上述的interpolation操作结束后，每个head将会产生一个长度为N的移位权值向量 st , st 是定义在所有可能的整形移位上的一个归一化分布。例如，假设移位的范围在-1到1之间（即最多可以前后移动一个位置），则移位值将有3种可能：-1,0,1，对应这3个值， st 也将有3个权值。那该怎么求出这些权值呢？比较常见的做法是，把这个问题看做一个多分类问题，在Controller中使用一个softmax层来产生对应位移的权重值。在论文中还实验了一种方法：在Controller中产生一个缩放因子，该因子为移位位置上均匀分布的下界。比如，如果该缩放因子值为6.7，那么 st(6)=0.3,st(7)=0.7 ， st 的其余分量为 0 （只取整数索引）。

st 生成之后，接下来就要使用 st 对 wgt 进行循环卷积操作，具体如下式：
w˜t(i)=∑j=0N−1wgt(j)st(i−j)
写成矩阵的形式如下：

原始可改写为： w˜t=Stwgt
由于卷积操作会使权值的分布趋于均匀化，这将导致本来集中于单个位置的焦点出现发散现象。为了解决这个问题，还需要对结果进行锐化操作。具体做法是Head产生一个因子 γt≥1 ，并通过如下操作来进行锐化：
wt(i)=w˜t(i)γt∑jw˜t(j)γt
通过上述操作后，权值分布将变得“尖锐”。
我们通过一个简单的例子来说明：
假设N=5，当前焦点为1，三个位置-1,0,1对应的权值为0.1,0.8,0.1, wgt=⎡⎣⎢⎢⎢⎢⎢⎢0.060.10.650.150.04⎤⎦⎥⎥⎥⎥⎥⎥ 则
St=⎡⎣⎢⎢⎢⎢⎢⎢st(0)st(1)st(2)st(3)st(4)st(4)st(0)st(1)st(2)st(3)st(3)st(4)st(0)st(1)st(2)st(2)st(3)st(4)st(0)st(1)st(1)st(2)st(3)st(4)st(0)⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢0.10.80.10000.10.80.10000.10.80.10.1000.10.80.80.1000.1⎤⎦⎥⎥⎥⎥⎥⎥
所以有：
w˜t=Stwgt=⎡⎣⎢⎢⎢⎢⎢⎢0.10.80.10000.10.80.10000.10.80.10.1000.10.80.80.1000.1⎤⎦⎥⎥⎥⎥⎥⎥×⎡⎣⎢⎢⎢⎢⎢⎢0.060.10.650.150.04⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢0.0530.0620.1510.5450.189⎤⎦⎥⎥⎥⎥⎥⎥
取 γt=2 ，
wt=w˜γtt∑jw˜t(j)γt=⎡⎣⎢⎢⎢⎢⎢⎢0.00780.01060.06300.82010.0986⎤⎦⎥⎥⎥⎥⎥⎥
可以看出来，经过锐化处理后 wt 不同元素直接的差异变得更明显了（即变得“尖锐”了），内存操作焦点将更加突出。

整个寻址的过程如下图：

通过上图的内存寻址系统，我们能够实现三种方式的内存访问：
1.直接通过内容寻址，即前边提到的Content-base方式；
2.通过对Content-base产生的权值进行选择和移位而产生新的寻址权值，在这种模式下，运行内存操作焦点跳跃到基于Content-base的下一个位置，这将使操作Head能够读取位于一系列相邻的内存块中的数据；
3.仅仅通过上一时刻的权值来生成新的操作地址权值，而不依赖任何当前的Content-base值。这将允许Head进行顺序迭代读取（比如可以通过多个时刻的连续迭代，读取内存中一个连续的数组）

3.3 控制器网络（Controller Network）

NTM的结构中存在很多的自由参数，比如内存的大小，读写头的数目，内存读取时的位移的范围。但是最重要的部分还是控制器的神经网络结构。比如，是选用递归网络还是前馈网络。如果选用LSTM，则其自有的隐层状态可以作为内存矩阵 Mt 的补充。如果把Controller与传统计算机的CPU进行类比，则 Mt 就相当于传统计算机的内存（RAM），递归网络中的隐层状态就相当于寄存器（Registers）,允许Controller混合跨越多个时间步的信息。另一方面，前馈网络可以通过在不同的时刻读取内存中相同的位置来模拟递归网络的特性。此外，基于前馈网络的Controller网络操作更为透明，因为此时的读写操作相比RNN的内部状态更容易解释。当然前馈网络的局限性主要在于同时存在的读写头数目有限。单一的Read Head每个时间步只能操作一个内存向量，而递归Controller则可通过内部存储器同时读取多个内存向量。