两个鸡蛋,100层楼,找出摔碎鸡蛋的最低楼层,所用的摔鸡蛋次数最少
题目:问题:一幢大楼共计100层,某种类型的鸡蛋从某一楼层及其以上楼层摔下来时会被打破,从该层楼(即临界楼层)以下楼层摔下该鸡蛋,鸡蛋不会出现破损。现给你2个完全一样的该种类型的鸡蛋,问:如何通过这2个鸡蛋找到该临界楼层时,所用的摔鸡蛋次数最少?
思考:给了我们2个鸡蛋,意思就很明显,有1个鸡蛋起到关键作用,它可以被打破,以告诉我们临界楼层大致在什么位置。
初探:看到这个题,首先想到的是二分搜索法,先从50楼摔下,分两种情况:
1.如果没碎:再从75楼(就是50+25=75)再次摔下。
2.如果碎了:第二个鸡蛋从25楼摔下……
如此去找,但是我们可以发现里面的漏洞,如果第二个鸡蛋从25楼摔下也碎了怎么办?就找不到可以摔碎鸡蛋的最低楼层了!
二分搜索失败,但我们从中找到一点启示:就是当我们找到一个鸡蛋可以摔碎的楼层区间时,不能从中再截取一段楼层再去扔,必须用顺序轮询法从低层到高层一层一层去找出那个楼层。(就像上面说的,如果鸡蛋从50楼摔下,碎了,那么第二个鸡蛋必须从一楼开始扔:一楼、二楼、三楼。。。。。。直到找出可以摔碎鸡蛋的楼层)。
所以思路出来了:开始可以分段去找出可以摔碎鸡蛋的楼层段(我们称之“高楼层分段找的次数”),然后再去轮询这个分界点以下的楼层段的每一层楼,看是在哪一层楼可以把鸡蛋摔碎(我们称之“低楼层轮询的次数”)。
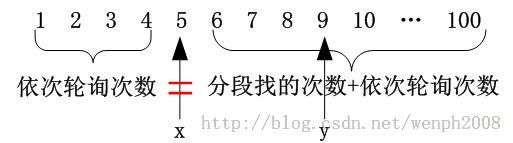
解答:我们使用暴力破解法,什么是暴力破解法?就是不存在侥幸心理(如果刚好碰到那个楼层就说我找到了摔碎鸡蛋的楼层就是侥幸心理),我们所假设的都是最坏情况下的查找次数。上图喽:
如果分得的第一段分界点在x=5处,那么最坏情况下x左边的查找次数应该等于x右边的查找次数,即上图中的“=”成立。
所以在x=5处分两种情况:鸡蛋碎了和没碎。两种情况的查找次数应该相等。
1. 如果鸡蛋没碎:那么说明所找楼层小于5,对于小于5的情况,必须轮询,也就是“低楼层轮询的次数”(参见上面思路),此时从1~4层轮询需要4次,即低楼层轮询次数=4。
2. 如果鸡蛋碎了:那么说明所找楼层大于5,对于大于5的情况,我们找楼层的次数=“高楼层分段找的次数”+“低楼层轮询的次数”。此时第二个分界点就是9!为什么呢?因为低楼层轮询次数=4,高楼层分段+低楼层轮询也一定要等于4,分段占去一次(在9这个位置),那么只能低楼层轮询=3,轮询6~8刚好等于3。
所以,如上图,最坏情况下:如果鸡蛋碎了,低楼层轮询4次。如果没碎,也是4次(9楼扔一次,假设没碎,然后6、7、8楼各扔一次,加起来4次,与低楼层次数相同)。
所以:
第一个分界点为5,5的左边要扔4次,5的右边也等于4次;第一个楼层段为5(1~5楼);
第二个分界点为9,9的左边要扔3次,9的右边也等于3次;第二个楼层段为4(6~9楼);
……
假设第一个分界点为x,则第一段楼层段就是x,而第二个楼层段就是x-1,第三个楼段是x-2,……那总共有多少个楼层段呢?有x个!
把所有楼层加起来小于总楼层100,就是x+(x-1)+(x-2)+……+[x-(x-1)]= x+(x-1)+(x-2)+……+1<=100。解出x=14。
检验:把答案列出来更直观:
第1次:14
第2次:+13=27
第3次:+12=39
第4次:+11=50
第5次:+10=60
第6次:+9=69
第7次:+8=77
第8次:+7=84
第9次:+6=90
第10次:+5=95
第11次:+4=99
第12次:+3=102
第13次:+2=104
第14次:+1=105