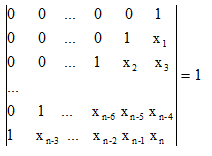【BZOJ3656】异或【扩展Lucas】【线性无关】
因为新数列中的数线性无关,即我们随意组合不会有重复结果,所以答案就是C(n, k) % p,因为p比较小,写个扩展Lucas就好了。
证明一下线性无关:
首先有两个引理:
定理1:一个n×n的矩阵A是非奇异的充要条件为 A的行列式不等于0。
定理2:令x1, x2, ..., xn为R^n中的n个向量,并令X = (x1, ...,xn)。向量x1,x2, ...,xn线性无关的充要条件是X为非奇异的。
因此我们只需要计算这个行列式的值,如果结果不为0,那么就是线性无关的。
我们把每个数都写成二进制的形式,把二进制的每一位都看成一维。
比如6 = 110(2),那么这个向量就是(1,1,0)。
举个例子,我们证明1,2,4是线性无关的,首先我们写出向量,分别为
(0,0,1),(0,1,0),(1,0,0)
得到行列式:
(注意这里是二进制的行列式。把加减法看做异或,把乘法看做与。)
上式不等于0,说明是线性无关的。
我们现在要证明新的数列1,3,5,10,17,39...是线性无关的,那么我们把新的数列表示为行列式。
表示成的行列式一定为这种形式:
(注意这里是二进制的行列式。把加减法看做异或,把乘法看做与。)
它的行列式等于-1,说明新数列线性无关。
Q:为什么反对角线上都是1?
A:考虑原数列的行列式,反对角线上都是1。每个数与它的约数位置异或,这个约数位置的数的二进制长度比这个数要短,无论怎么异或都不会改变这个1。
Q:为什么这个行列式等于-1?
A:因为只有反对角线上没有0。
Q:为什么有x。。
A:因为异或后的结果我也不知道是0是1呀...
Q.E.D.
直接上模板即可。
#include <cstdio>
typedef unsigned long long ULL;
typedef long long LL;
inline void exgcd(ULL a, ULL b, LL &x, LL &y) {
b ? (exgcd(b, a % b, y, x), y -= a / b * x) : (x = 1, y = 0);
}
inline ULL qpow(ULL x, ULL n, ULL p) {
ULL ans = 1;
for(ULL t = x; n; n >>= 1, t = x * x % p) if(n & 1) ans = ans * t % p;
return ans;
}
inline ULL c1(ULL n, ULL p, ULL pk) {
if(n == 0) return 1;
ULL ans = 1;
for(ULL i = 2; i <= pk; i++) if(i % p) ans = ans * i % pk;
ans = qpow(ans, n / pk, pk);
for(ULL k = n % pk, i = 2; i <= k; i++) if(i % p) ans = ans * i % pk;
return ans * c1(n / p, p, pk) % pk;
}
inline ULL inv(ULL a, ULL m) {
LL x, y;
exgcd(a, m, x, y);
if(x < 0) x += m;
return x;
}
inline ULL calc(ULL n, ULL m, ULL p, ULL pi, ULL pk) {
ULL a = c1(n, pi, pk), b = c1(m, pi, pk), c = c1(n - m, pi, pk), k = 0;
for(ULL i = n; i; i /= pi) k += i / pi;
for(ULL i = m; i; i /= pi) k -= i / pi;
for(ULL i = n - m; i; i /= pi) k -= i / pi;
ULL ans = a * inv(b, pk) % pk * inv(c, pk) % pk * qpow(pi, k, pk) % pk;
return ans * (p / pk) % p * inv(p / pk, pk) % p;
}
int main() {
ULL n, m, p;
scanf("%llu%llu%llu", &n, &m, &p);
ULL ans = 0;
for(ULL i = 2, x = p; x > 1; i++) if(x % i == 0) {
ULL k;
for(k = 1; x % i == 0; x /= i) k *= i;
ans = (ans + calc(n, m, p, i, k)) % p;
}
printf("%llu\n", ans);
return 0;
}