计算机视觉与模式识别（2）—— A4纸矫正

        上次写了A4纸的边缘提取，发现我的代码还是存在着很多的问题，比如令人诟病的静态阈值，还有非结构化的编程风格。于是我重新整理了一下，把A4纸边缘提取的代码整合为一个类。不过那个该死的阈值啊，我暂时还没有找到完美的方法，使得适用于所有的图像_(:з」∠)_。

        优化的方法倒是有一点，那就是降低标准，择优录取。也就是把阈值调得很低，但是峰值提取的结果只取最优的4个。当然啦，这种方法偶尔会取到奇怪的边缘，而且由于阈值的降低，导致的计算量也成倍增长，特别是Hough变换。但综合来看，鲁棒性还是增强了不少。

        另外，大家可以搜下有关 “边缘提取动态阈值获取” 的论文。梯度阈值动态的一个简单方法，就是取所有像素点梯度的平均值，至于效果怎样，有待大家尝试哦~

        那么，在上一节的基础上，我们还能做什么呢？

        我们现在只是知道了A4纸的边缘和角点，每一张A4纸都处于不同的的角度、位置，甚至有着不同的形状。这些“畸形”的A4纸不利于我们进一步的图像处理，因此需要把它们矫正成统一的矩形。

        输入图像：

        普通A4打印纸，上面可能有手写笔记或者打印内容，但是拍照时可能角度不正。

                

        输出图像：

        已经矫正好的标准普通A4纸(210:297)，并裁掉无用的其他内容，只保留完整的A4纸张。

                

        

        实验中，我使用了两种方法，一种是Projective Transform（仿射变换），一种是Morphing（变形）。

        两种方法各有优缺点，其中仿射变换处理速度快，矫正图片准确，但是涉及矩阵演算。Morphing的图像准确度没有仿射变换高，但是原理通俗易懂，不怎么需要演算。

        方法一：Projective Transform

        主要参考这篇博客：http://blog.csdn.net/xiaowei_cqu/article/details/26471527

        但是有几个错误需要指出来，不为0时，应得到：

        a11= x1 - x0 +a13* x1             a12= y1 - y0 +a13* y1        a13=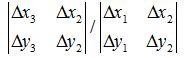 

        a21 = x3 - x0 + a23 * x3           a22= y3 - y0 +a23* y3        a23= 

        a31 = x0                                   a32 = y0                            a33 = 1

        关键代码：

Matrix3x3 A4ShapeCorrect::squareToQuadrilateral(double x0, double y0, double x1, double y1, double x2,
	double y2, double x3, double y3) 
{
	double dx3 = x0 - x1 + x2 - x3;
	double dy3 = y0 - y1 + y2 - y3;
	if (dx3 == 0.0f && dy3 == 0.0f) 
	{
		Matrix3x3 result(x1 - x0, y1 - y0, 0, 
				 x2 - x1, y2 - y1, 0, 
				 x0, y0, 1);
		return result;
	}
	else 
	{
		double dx1 = x1 - x2;
		double dx2 = x3 - x2;
		double dy1 = y1 - y2;
		double dy2 = y3 - y2;
		double denominator = dx1 * dy2 - dx2 * dy1;
		double a13 = (dx3 * dy2 - dx2 * dy3) / denominator;
		double a23 = (dx1 * dy3 - dx3 * dy1) / denominator;
		Matrix3x3 result(x1 - x0 + a13 * x1, y1 - y0 + a13*y1, a13,
				 x3 - x0 + a23*x3, y3 - y0 + a23*y3, a23, 
				 x0, y0, 1);
		return result;
	}
}

        计算出了变换矩阵的系数后，只需要应用到每个像素坐标就好了。 要注意方向：从目标像素映射到原像素，并且计算插值。

Matrix3x3 H = squareToQuadrilateral(dots[0]->x, dots[0]->y, dots[1]->x, dots[1]->y,
				    dots[2]->x, dots[2]->y, dots[3]->x, dots[3]->y);

/* Method 1: Projective Transforming */
cimg_forXY(*target, x, y)
{
	double _x = (double)x / _width;
	double _y = (double)y / _height;
	double denominator = H.a13 * _x + H.a23 * _y + H.a33;
	double tx = (H.a11 * _x + H.a21 * _y + H.a31) / denominator;
	double ty = (H.a12 * _x + H.a22 * _y + H.a32) / denominator;
	cimg_forC(*target, c)
		(*target)(x, y, 0, c) = bilinear(img, tx, ty, 0, c);
}

        方法二：Morphing

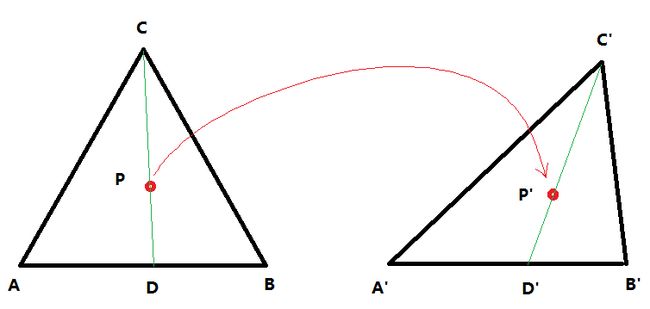
        针对三角形进行Morph变换，思路类似双线性插值：

        如何计算P'的坐标:：DA / BA = D'A' / B'A'  ， PC / DC = P'C' / D'C'， 其中ABC、A'B'C'和P坐标已知。

        有了计算变换三角形位置的方法，我们就可以把原A4纸延对角线切割成两个三角形，把目标图形也延对角线切割成两个三角形，然后分别对这两个三角形内的像素点坐标做Morph变换即可。

        其中还要解决的问题是如何判断一个点在三角形内，参考博客：http://www.cnblogs.com/graphics/archive/2010/08/05/1793393.html

        我采用了第3种方法。

        关键代码：

Dot* A4ShapeCorrect::morph(Triangle source, Triangle target, Dot p)
{
	Dot a = source.a, b = source.b, c = source.c;
	Dot at = target.a, bt = target.b, ct = target.c;

	if (p == a) return new Dot(at.x, at.y);
	if (p == b) return new Dot(bt.x, bt.y);
	if (p == c) return new Dot(ct.x, ct.y);

	Line cp(c, p);
	Line ab(a, b);
	Dot* d = cp.intersect(ab);
	// DA / BA
	double ABrate = (b.x - a.x != 0) ? (d->x - a.x) / (b.x - a.x) : (d->y - a.y) / (b.y - a.y);
	// PC / DC
	double CDrate = (d->x - c.x != 0) ? (p.x - c.x) / (d->x - c.x) : (p.y - c.y) / (d->y - c.y);

	double dtx = ABrate*(bt.x - at.x) + at.x;
	double dty = ABrate*(bt.y - at.y) + at.y;

	double ptx = CDrate*(dtx - ct.x) + ct.x;
	double pty = CDrate*(dty - ct.y) + ct.y;
	return new Dot(ptx, pty);
}

        同样要注意方向：从目标像素映射到原像素，并且计算插值。

/* Method 2: Morphing */
Dot At(0, 0);
Dot Bt(target->width() - 1, 0);
Dot Ct(target->width() - 1, target->height() - 1);
Dot Dt(0, target->height() - 1);

Dot A(dots[0]->x, dots[0]->y);
Dot B(dots[1]->x, dots[1]->y);
Dot C(dots[2]->x, dots[2]->y);
Dot D(dots[3]->x, dots[3]->y);

cimg_forXY(*target, x, y)
{
	Dot P(x, y), *p = NULL;
	if (pointInTriangle(Triangle(At, Bt, Ct), P))
		p = morph(Triangle(At, Bt, Ct), Triangle(A, B, C), P);
	else if (pointInTriangle(Triangle(At, Ct, Dt), P))
		p = morph(Triangle(At, Ct, Dt), Triangle(A, C, D), P);
	if (p != NULL)
	{
		cimg_forC(*target, c)
			(*target)(x, y, 0, c) = bilinear(img, p->x, p->y, 0, c);
	}
}

        

        对于以上两种方法，都涉及一个前提：我们找到的原图A4纸角点必须按顺序ABCD排列，或者我们至少知道各角点对应的A4纸方位。

        我的方法是4个点先按y轴排序，y最小的不是A点就是B点，然后找跟这点最近的点，找到后这两个点就分别是A和B（事实上并不一定，比如扁菱形）。接着判断矩形是横的还是竖的，然后准确判断AB位置，最后准确判断CD位置。只能说So far so good!

void A4ShapeCorrect::reorderDots(std::vector<Dot*>& dots)
{
	std::sort(dots.begin(), dots.end(), [](const Dot* a, const Dot* b) { return a->y < b->y; });
	double min = DBL_MAX;
	int temp;
	for (int i = 1; i < dots.size(); ++i)
	{
		double dis = dots[0]->distance(*dots[i]);
		if (min > dis)
		{
			min = dis;
			temp = i;
		}
	}
	std::swap(dots[1], dots[temp]);
	if (dots[1]->y > dots[2]->y || dots[1]->y > dots[3]->y)
	{
		std::swap(dots[0], dots[1]);
		if (dots[2]->y > dots[3]->y)
		{
			std::swap(dots[2], dots[3]);
		}
	}
	else
	{
		if (dots[0]->x > dots[1]->x)
		{
			std::swap(dots[0], dots[1]);
		}
		if (dots[2]->x < dots[3]->x)
		{
			std::swap(dots[2], dots[3]);
		}
	}
}