经典算法——最长回文子序列
最长回文子序列LPS(Longest Palindromic Subsequence)问题
一个字符串有许多子序列,比如字符串cabbeaf,它的子序列有c、abb、e、a、f,可以通过删除某些字符而变成回文字符串,字符串“cabbeaf”,删掉‘c’、'e'、‘f’后剩下的子串“abba”就是回文字符串,也是其中最长的回文子序列。注意和最长回文子串点击打开链接的区别,最长回文子串必须是连续的,这里的最长回文子序列,可以是不连续的,这就是最长回文子序列LPS问题。
方法一:递归方法
str[0...n-1]是给定的字符串序列,长度为n,假设lps(0,n-1)表示序列str[0...n-1]的最长回文子序列的长度。
1.如果str的最后一个元素和第一个元素是相同的,则有:lps(0,n-1)=lps(1,n-2)+2;例如字符串序列“AABACACBA”,第一个元素和最后一个元素相同,其中lps(1,n-2)表示红色部分的最长回文子序列的长度;
2.如果str的最后一个元素和第一个元素是不相同的,则有:lps(0,n-1)=max(lps(1,n-1),lps(0,n-2));例如字符串序列“ABACACB”,其中lps(1,n-1)表示去掉第一元素的子序列,lps(0,n-2)表示去掉最后一个元素的子序列。
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
//递归方法,求解最长回文子序列
int lps(char *str, int i, int j)
{
if (i == j)
return 1; //只有一个元素,回文长度为1
if (i > j) return 0; //因为只计算序列str[i....j]
//如果首尾相同
if (str[i] == str[j])
return lps(str, i + 1, j - 1) + 2;
//如果首尾不同
return max(lps(str, i, j - 1), lps(str, i + 1, j));
}
int main()
{
char str[] = "cabbeaf";
int n = strlen(str);
int res = lps(str, 0, n - 1);
cout << res<< endl;
getchar();
return 0;
}
重叠子问题
但是通过上面递归的方法,会出现很多重复的计算,比如上面的L(1,4),所以可以采用动态规划的方法求解
方法二:动态规划方法
通过自下而上的方式记录子问题的最优解
#include<iostream>
#include<algorithm>
using namespace std;
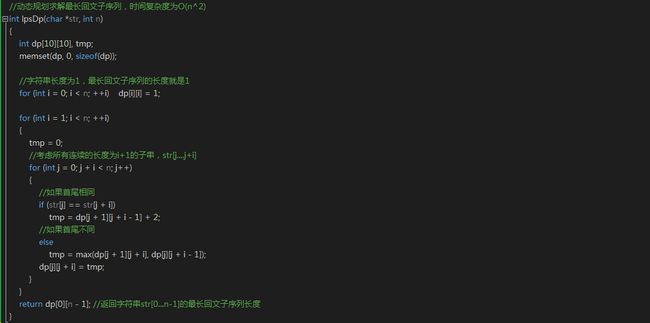
//动态规划求解最长回文子序列,时间复杂度为O(n^2)
int lpsDp(char *str, int n)
{
int dp[10][10], tmp;
memset(dp, 0, sizeof(dp));
for (int i = 0; i < n; ++i) dp[i][i] = 1;
for (int i = 1; i < n; ++i)
{
tmp = 0;
//考虑所有连续的长度为i+1的子串,str[j....j+i]
for (int j = 0; j + i < n; j++)
{
//如果首尾相同
if (str[j] == str[j + i])
tmp = dp[j + 1][j + i - 1] + 2;
//如果首尾不同
else
tmp = max(dp[j + 1][j + i], dp[j][j + i - 1]);
dp[j][j + i] = tmp;
}
}
return dp[0][n - 1]; //返回字符串str[0...n-1]的最长回文子序列长度
}
int main()
{
char str[10] = "cabbeaf";
int res = lpsDp(str, strlen(str));
cout << res << endl;
getchar();
return 0;
}
参考:http://www.geeksforgeeks.org/dynamic-programming-set-12-longest-palindromic-subsequence/
附:腾讯2016实习笔试编程题
所谓回文字符串,就是一个字符串,从左到右读和从右到左读是完全一样的,比如“aba”、“c”,对于一个字符串,可以通过删除某些字符而变成回文字符串,如“cabebaf”,删除'c'、'e'、‘f’后剩下子串“abba”就是回文字符串。
要求,给定任意一个字符串,字符串最大长度1000,计算出最长的回文字符串长度。
如“cabebaf”的回文串包括“c”、“aba”、“abba”等,最长回文“abba”长度为4。
输入:字符串
输出:最大的回文字符长度。
示例:
输入:cabbeaf
输出:4
#include<iostream>
#include<algorithm>
using namespace std;
#define MAXN 1000
//动态规划求解最长回文子序列,时间复杂度为O(n^2)
int lpsDp(char *str, int n)
{
int dp[MAXN>>1][MAXN>>1], tmp;
memset(dp, 0, sizeof(dp));
//字符串长度为1,最长回文子序列的长度就是1
for (int i = 0; i < n; ++i) dp[i][i] = 1;
for (int i = 1; i < n; ++i)
{
tmp = 0;
//考虑所有连续的长度为i+1的子串,str[j....j+i]
for (int j = 0; j + i < n; j++)
{
//如果首尾相同
if (str[j] == str[j + i])
tmp = dp[j + 1][j + i - 1] + 2;
//如果首尾不同
else
tmp = max(dp[j + 1][j + i], dp[j][j + i - 1]);
dp[j][j + i] = tmp;
}
}
return dp[0][n - 1]; //返回字符串str[0...n-1]的最长回文子序列长度
}
int main()
{
char str[MAXN];
while (cin >> str)
{
int res = lpsDp(str, strlen(str));
cout << res << endl;
}
getchar();
return 0;
}