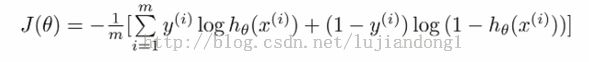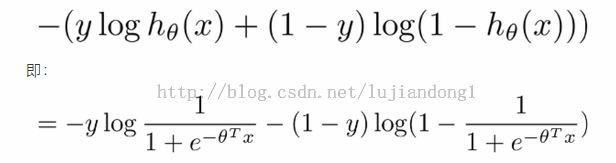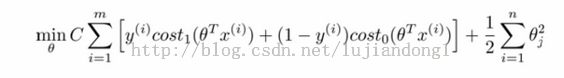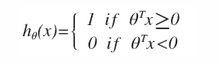machine learning week7 学习笔记 SVM 习题解答
先附上作业的下载地址:http://download.csdn.net/detail/lujiandong1/8610685
支持向量机,SVM,是非常强大且流行的算法,在一些情况下,能面向一些复杂的非线性问题提供比逻辑回归或神经网络要更加简洁的解决方案。
week7视频中,12 - 3 - Mathematics Behind Large Margin Classification (Optional) (20 min)对支撑向量机是大间距分类器,有比较形象的解释。
1.1优化目标(Optimization Objective)
我们分y=1和y=0两种情况讨论:
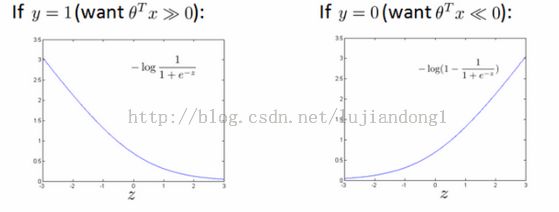
- y=1时,希望假设h θ (x)预测的值尽可能接近1,即希望z=θ T X尽可能地大
- y=0时,希望假设h θ (x)预测的值尽可能接近0,即希望z=θ T X尽可能地小
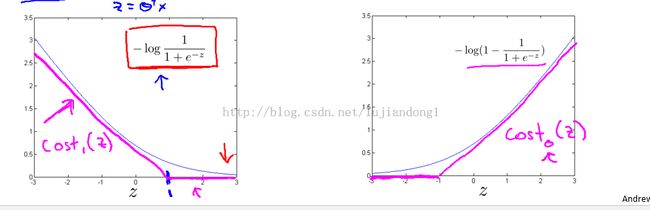
- 当y=1时, 我们希望构建新的代价函数如cost 1 (z)所示,当z>=1时,cost 1 (z)=0
- 当y=0时,我们希望构建新的代价函数如cost 0 (z)所示,当z<=-1时,cost 0 (z)=0
- 因为1/m实际上不影响最优化的结果,将其去掉。
- 因为归一化参数λ控制的是归一化的这一项在整个代价函数中占的比例,对于支持向量机,我们想要控制的是新构建的代价函数部分,因此我们去掉λ的同时给第一项乘以一个常数C,相当于我们将整个代价函数除以了λ,且C=1/λ。
1.2支持向量机判定边界( SVM Decision Boundary)
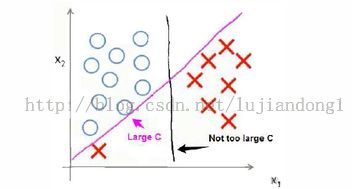
支持向量机有的时候也被称为 最大间隔分类器 (Large Margin Classifier),其原因是: 支持向量机可以尝试发现一个与样本数据集之间有着最大间隔的判定边界。回顾 C=1/λ,因此:
- C较大时,相当于λ较小,可能会导致过拟合,高偏倚(高方差)。
- C较小时,相当于λ较大,可能会导致低拟合,高偏差()。
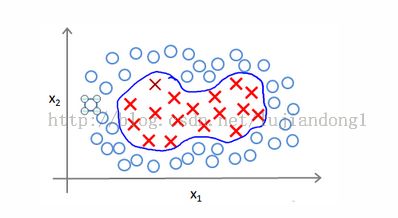
1.3 核函数 ( Kernel s)
我们可以利用 核函数 来计算出新的特征。
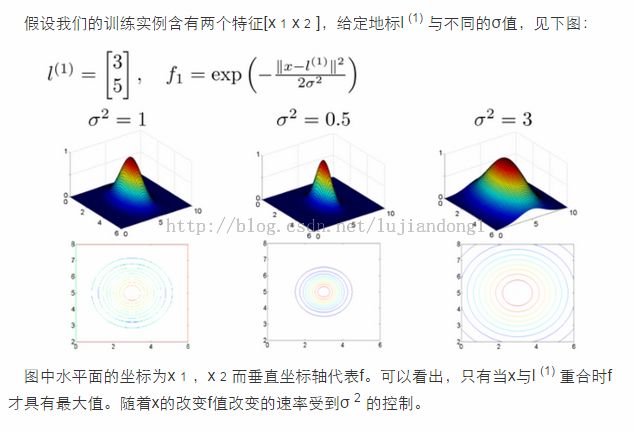
给定一个训练实例x,我们利用x的各个特征与我们预先选定的 地标 (landmarks)l(1) ,l (2) ,l (3) 的近似程度来选取新的特征f 1 ,f 2 ,f 3
这些地标的作用是什么?如果一个训练实例x与地标L之间的距离近似于0,则新特征f近似于e -0 =1,如果训练实例x与地标L之间距离较远,则f近似于e-(一个较大的数)=0。
如何选择地标?
我们通常是根据训练集的数量选择地标的数量,即如果训练集中有m个实例,则我们选取m个地标,并且令:l (1) =x (1) ,l (2) =x (2) ,...,l (m) =x (m) 。这样做的好处在于:现在我们得到的新特征是建立在原有特征与训练集中所有其他特征之间距离的基础之上的,即:
下面我们将核函数运用到支持向量机中,修改我们的支持向量机假设为:
另外,支持向量机也可以不使用核函数,不使用核函数又称为 线性核函数 (linear kernel),当我们不采用非常复杂的函数,或者我们的训练集特征非常多而实例非常少的时候,可以采用这种不带核函数的支持向量机。
下面是支持向量机的两个参数C和σ的影响:
- C较大时,相当于λ较小,可能会导致过拟合,高偏倚
- C较小时,相当于λ较大,可能会导致低拟合,高偏差
- σ较大时,导致高偏倚
- σ较大时,导致高偏差

多类分类问题
假设我们利用之前介绍的一对多方法来解决一个多类分类问题。如果一共有k个类,则我们需要k个模型,以及k个参数向量θ。我们同样也可以训练k个支持向量机来解决多类分类问题。但是大多数支持向量机软件包都有内置的多类分类功能,我们只要直接使用即可。
解释:即第一步将第1类看成一类,第{2:K}类看成第二类,训练一个SVM,然后把第2类看成一类,第{1,3:K}类看成第二类,训练第二个SVM,得到K个SVM,然后计算每个SVM的hθ(x),哪个SVM的hθ(x)比较大,就判为哪一类。
1.4逻辑回归与支持向量机
从逻辑回归模型,我们得到了支持向量机模型,在两者之间,我们应该如何选择呢?
下面是一些普遍使用的准则:
- 如果相较于m而言,n要大许多,即训练集数据量不够支持我们训练一个复杂的非线性模型,我们选用逻辑回归模型或者不带核函数的支持向量机。
- 如果n较小,而且m大小中等,例如n在1-1000之间,而m在10-10000之间,使用带高斯核函数的支持向量机。
- 如果n较小,而m较大,例如n在1-1000之间,而m大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
值得一提的是,神经网络在以上三种情况下都可能会有较好的表现,但是训练神经网络可能非常慢,选择支持向量机的原因主要在于它的代价函数是凸函数,不存在局部最小值。