基于字符串的编辑距离
最近因为项目需要对一个web网页变更进行实时监控,之前项目组有人采用的是比较简单 的文本对比的方式,只要发现文本中一处发生变动就进行告警,最后导致的结果就是误报的情况比较多,比如在对首页进行监控时,后台对用户访问量的统计会在首页实时更新,这样就会被当做网站被改动来处理了,而这并不是我们所需要的,因为我们感兴趣的不是网页动态数据区域的变化,这样我们最终要解决的就是怎么来分离网页的动态区域和静态区域。
动态区域和静态区域的分离技术应用在很多方向,数据挖掘方面应用的较广,如网页数据抽取、网页聚类、网页篡改等等。
在参考了以下论文《 web网页中动态数据区域的识别去抽取》《基于模板的网页数据抽取》《基于局部变化性的网页篡改识别模型及方法》《网页篡改系统的研究与实现》之后,大体思路就是采用编辑距离来计算树或字符串的相似度,对字符串的编辑距离计算相当于计算一维向量的编辑距离。
本系统大体也是采用了dom遍历比较以及节点标记的方式来实现,最终形成一个节点集合,然后对形成的节点集合中相邻的节点进行合并形成网页模板。这个也是我大体的方案。
第一个难点是如何去遍历两颗dom树,首先我们先解决比较两个节点集合中的变化节点,如果采用论文中的for for语句来遍历的话会出现相邻节点顺序变化却无法检测到的情况,并且节点会重复遍历,而我们想要找出插入、删除的节点,修改的节点相当于执行了删除插入操作,而我们这里将标签 名没变化内容或属性变化的情况称作修改操作。原先我们采用在for for循环中引入了一个移动标记位来解决也可以一次找出变化的节点,后来发现编辑距离不仅可以解决相似度的问题,而且通过矩阵回溯也可以一次找出变化的节点,一下是标准的字符串编辑距离算法。
值得说明的是,编辑距离计算的前提是只允许插入、删除、修改操作来达到字符串转换的目的。
而我们的算法 也只需要这3中操作,而编辑距离算法本身却不之局限这3种操作,具体可参考http://blog.csdn.net/mishifangxiangdefeng/article/details/7925025
而我们也可以去掉某种操作或该重新定义某种操作的行为,一下是标准的编辑距离计算方法。
// Strings of size m and n are passed.
// Construct the Table for X[0...m, m+1], Y[0...n, n+1]
int EditDistanceDP(char X[], char Y[])
{
// Cost of alignment
int cost = 0;
int leftCell, topCell, cornerCell;
int minCell = 0;
int m = strlen(X)+1;
int n = strlen(Y)+1;
// T[m][n]
int *T = (int *)malloc(m * n * sizeof(int));
//用于矩阵回溯
int *operation = (int *)malloc(m * n * sizeof(int));
// Initialize table
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
*(T + i * n + j) = SENTINEL;
// Set up base cases
// T[i][0] = i
for(int i = 0; i < m; i++){
*(T + i * n) = i;
*(operation+ i*n)=3;
}
// T[0][j] = j
for(int j = 0; j < n; j++){
*(T + j) = j;
*(operation+j)=2;
}
*operation=0;
// Build the T in top-down fashion
for(int i = 1; i < m; i++)
{
for(int j = 1; j < n; j++)
{
leftCell = *(T + i*n + j-1);
leftCell += EDIT_COST;
topCell = *(T + (i-1)*n + j);
topCell += EDIT_COST;
cornerCell = *(T + (i-1)*n + (j-1) );
// edit[(i-1), (j-1)] = 0 if X[i] == Y[j], 1 otherwise
cost = (X[i-1] == Y[j-1]?0:1);
cornerCell += cost; // may be replace
//如果不回溯则直接调用该函数
//minCell = Minimum(leftCell, topCell, cornerCell);
if(topCell>leftCell)
{
if(cornerCell>leftCell)
{
minCell=leftCell;
*(operation + (i)*n + (j))=2;
}
else
{
minCell=cornerCell;
*(operation + (i)*n + (j))=cost;
}
}
else
{
if(cornerCell>topCell)
{
minCell=topCell;
*(operation + (i)*n + (j))=3;
}
else
{
minCell=cornerCell;
*(operation + (i)*n + (j))=cost;
}
}
*(T + (i)*n + (j)) = minCell;
}
}
// 结果存储在 T[m][n]
cost = *(T + m*n - 1);
backtrace(operation, X, Y);
free(T);
return cost;
}通过矩阵回溯可计算出变化的位置
void backtrace(int* operation, char* a, char* b)
{
int insertion=0,deletion=0,substitution=0;
int i,j;
int len1=strlen(a);
int len2=strlen(b);
int m = strlen(a)+1;
int n = strlen(b)+1;
for (i=len1,j=len2;i>=0&&j>=0;)
{
switch(*(operation+i*n+j))
{
case 0:
//printf("(%d,%d) right\n",i,j);
printf("pos %d right\n",i);
i--;
j--;
continue;
case 1:
//printf("(%d,%d) substitute\n",i,j);
printf("pos %d substitute (%c-->%c)\n",i,a[i-1],b[j-1]);
i--;
j--;
substitution++;
continue;
case 2:
//printf("(%d,%d) insert\n",i,j);
printf("pos %d insert (%c)\n",i,b[j-1]);
j--;
insertion++;
continue;
case 3:
//printf("(%d,%d) delete\n",i,j);
printf("pos %d delete (%c)\n",i,a[i-1]);
i--;
deletion++;
continue;
}
}
printf("insert:%d,delete:%d,substitute:%d\n",insertion,deletion,substitution);
}
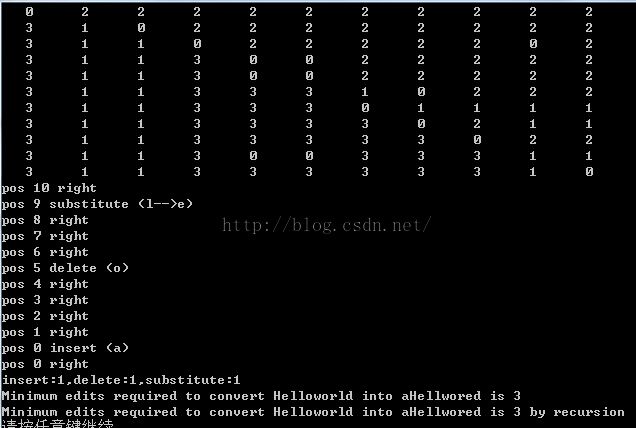
下面是计算HelloWorld和aHelloWored的编辑距离结果显示,图中矩阵为回溯矩阵
系统对算法进行改进后重新定义了编辑操作,不是比较字符串而是比较节点集合,今天就先写到这,下一篇文章中会将基于树的编辑距离计算和dom树遍历过程以及网页模板训练都写出来供大家参考学习。