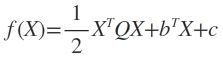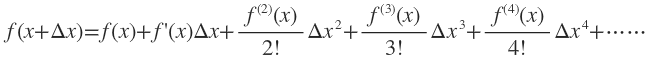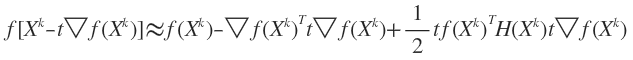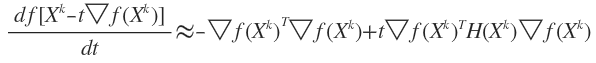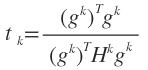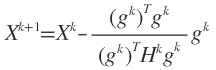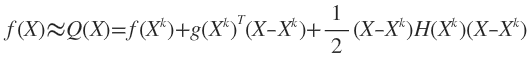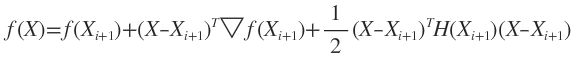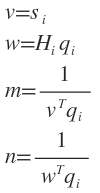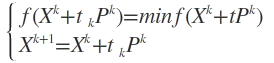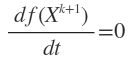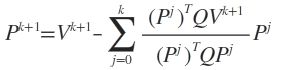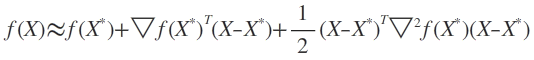最优化算法总结

梯度的方向与等值面垂直。

二次收敛是指一个算法用于具有正定二次型函数时，在有限步可达到它的极小点。二次收敛与二阶收敛没有尽然联系，更不是一回事，二次收敛往往具有超线性以上的收敛性。一阶收敛不一定是线性收敛。

解释一下什么叫正定二次型函数：

n阶实对称矩阵Q，对于任意的非0向量X，如果有X^TQX>0，则称Q是正定矩阵。

对称矩阵Q为正定的充要条件是：Q的特征值全为正。

二次函数，若Q是正定的，则称f(X)为正定二次函数。

黄金分割法

黄金分割法适用于任何单峰函数求极小值问题。

求函数在[a,b]上的极小点，我们在[a,b]内取两点c,d，使得a<c<d<b。并且有

1）如果f(c)<f(d)，则最小点出现在[a,d]上，因此[a,d]成为下一次的搜索区间。

2）如果f(c)>f(d)，则[c,b]成为下一次的搜索区间。

假如确定了[a,d]是新的搜索区间，我们并不希望在[a,d]上重新找两个新的点使之满足(1)式，而是利用已经抗找到有c点，再找一个e点，使满足：

可以解得r=0.382，而黄金分割点是0.618。

练习：求函数f(x)=x*x-10*x+36在[1,10]上的极小值。

#include<stdio.h>
#include<math.h>
#include<limits.h>

double  func( double  x){
    return  x*x-10*x+36;
}

void  main(){
    double  zeta=0.001;
    double  a=1.0,b=10.0;
    double  t1=a-1;
    double  t2=b+1;
    double  v1=0.0;
    double  v2=0.0;
    double  min_value=INT_MAX;
    int  iteration=0;
    while (++iteration){
        if (t1==a-1){
            t1=a+0.382*(b-a);
            v1=func(t1);
        }
        if (t2==b+1){
            t2=a+0.618*(b-a);
            v2=func(t2);
        }
        if (v1<v2){
            min_value=v1;
            b=t2;
            t2=t1;
            v2=v1;
            t1=a-1;
        }
        else {
            min_value=v2;
            a=t1;
            t1=t2;
            v1=v2;
            t2=b+1;
        }
        if ( fabs (b-a)<zeta)
            break ;
        printf ( "当前极小值%f\n" ,min_value);
    }
    printf ( "迭代次数%d\n" ,iteration);
    printf ( "极小值%f\n" ,min_value);
}

最速下降法

泰勒级数告诉我们：

其中Δx可正可负，但必须充分接近于0。

X沿D方向移动步长a后，变为X+aD。由泰勒展开式：

目标函数：

a确定的情况下即最小化：

向量的内积何时最小？当然是两向量方向相反时。所以X移动的方向应该和梯度的方向相反。

接下来的问题是步长a应该怎么定才能使迭代的次数最少？

若f(X)具有二阶连续偏导，由泰勒展开式可得：

H是f(X)的Hesse矩阵。 

可得最优步长：

g是f(X)的梯度矩阵。

此时：

可见最速下降法中最优步长不仅与梯度有关，而且与Hesse矩阵有关。

练习：求函数f(x1,x2)=x1*x1+4*x2*x2在极小点，以初始点X0=(1,1)T。

#include"matrix.h"

#include<iostream>

#include<iomanip>

#include<cmath>

#include<limits>

#include<cassert>



using  namespace  std;



const  int  SIZE=2;

const  double  ZETA=0.001;



inline  double  func(Matrix< double > &X){

    assert (SIZE==X.getRows());

    double  x1=X.get(0,0);

    double  x2=X.get(1,0);

    return  x1*x1+4*x2*x2;

}



inline  Matrix< double > gradient(Matrix< double > &X){

    assert (SIZE==X.getRows());

    double  x1=X.get(0,0);

    double  x2=X.get(1,0);

    Matrix< double > rect(SIZE,1);

    rect.put(0,0,2*x1);

    rect.put(1,0,8*x2);

    return  rect;

}



inline  Matrix< double > Hesse(Matrix< double > &X){

    Matrix< double > rect(SIZE,SIZE);

    rect.put(0,0,2);

    rect.put(0,1,0);

    rect.put(1,0,0);

    rect.put(1,1,8);

    return  rect;

}



int  main( int  agrc, char  *argv[]){

    Matrix< double > X(SIZE,1);

    X.put(0,0,1);

    X.put(1,0,1);

    int  iteration=0;

    double  value=func(X);

    double  newValue=numeric_limits< double >::max();

    while (++iteration){

        Matrix< double > G=gradient(X);

        double  factor=((G.getTranspose()*G).get(0,0))/((G.getTranspose()*Hesse(X)*G).get(0,0));

        for ( int  i=0;i<G.getRows();++i)

                for ( int  j=0;j<G.getColumns();++j)

                        G.put(i,j,G.get(i,j)*factor);

        Matrix< double > newX=X-G;

        //cout<<"X=["<<newX.get(0,0)<<","<<newX.get(1,0)<<"]"<<endl;

        newValue=func(newX);

        if ( fabs (newValue-value)<ZETA)

                break ;

        else {

                X=newX;

                value=newValue;

        }

        //cout<<"本次迭代找到的极小值"<<value<<endl;

    }

    cout<< "迭代次数" <<iteration<<endl;

    cout<< "极小值" <<value<<endl;

    return  0;

}

梯度下降法开始的几步搜索，目标函数下降较快，但接近极值点时，收敛速度就比较慢了，特别是当椭圆比较扁平时，收敛速度就更慢了。

另外最速下降法是以函数的一次近似提出的，如果要考虑二次近似，就有牛顿迭代法。

牛顿迭代法

在点X^k处对目标函数按Taylar展开：

 

 令

得

即

可见X的搜索方向是，函数值要在此方向上下降，就需要它与梯度的方向相反，即。所以要求在每一个迭代点上Hesse矩阵必须是正定的。

练习：求的极小点，初始点取X=(0,3)。

#include"matrix.h"
#include<iostream>
#include<iomanip>
#include<cmath>
#include<limits>
#include<cassert>

using  namespace  std;

const  int  SIZE=2;
const  double  ZETA=0.001;

inline  double  func(Matrix< double > &X){
    assert (SIZE==X.getRows());
    double  x1=X.get(0,0);
    double  x2=X.get(1,0);
    return  pow (x1-2,4)+ pow (x1-2*x2,2);
}

inline  Matrix< double > gradient(Matrix< double > &X){
    assert (SIZE==X.getRows());
    double  x1=X.get(0,0);
    double  x2=X.get(1,0);
    Matrix< double > rect(SIZE,1);
    rect.put(0,0,4* pow (x1-2,3)+2*(x1-2*x2));
    rect.put(1,0,-4*(x1-2*x2));
    return  rect;
}

inline  Matrix< double > Hesse(Matrix< double > &X){
    Matrix< double > rect(SIZE,SIZE);
    double  x1=X.get(0,0);
    double  x2=X.get(1,0);
    rect.put(0,0,12* pow (x1-2,2)+2);
    rect.put(0,1,-4);
    rect.put(1,0,-4);
    rect.put(1,1,8);
    return  rect;
}

int  main( int  agrc, char  *argv[]){
    Matrix< double > X(SIZE,1);
    X.put(0,0,0);
    X.put(1,0,3);
    int  iteration=0;
    double  value=func(X);
    double  newValue=numeric_limits< double >::max();
    while (++iteration){
        Matrix< double > G=gradient(X);
        Matrix< double > H=Hesse(X);
        Matrix< double > newX=X-H.getInverse()*G;
        cout<< "X=[" <<newX.get(0,0)<< "," <<newX.get(1,0)<< "]" <<endl;
        newValue=func(newX);
        if ( fabs (newValue-value)<ZETA)
            break ;
        else {
            X=newX;
            value=newValue;
        }
        cout<< "本次迭代找到的极小值" <<value<<endl;
    }
    cout<< "迭代次数" <<iteration<<endl;
    cout<< "极小值" <<value<<endl;
    return  0;
}

 牛顿法是二次收敛的，并且收敛阶数是2。一般目标函数在最优点附近呈现为二次函数，于是可以想像最优点附近用牛顿迭代法收敛是比较快的。而在开始搜索的几步，我们用梯度下降法收敛是比较快的。将两个方法融合起来可以达到满意的效果。

收敛快是牛顿迭代法最大的优点，但也有致命的缺点：Hesse矩阵及其逆的求解计算量大，更何况在某个迭代点X^k处Hesse矩阵的逆可能根本就不存在（即Hesse矩阵奇异），这样无法求得X^k+1。

拟牛顿法

Hesse矩阵在拟牛顿法中是不计算的，拟牛顿法是构造与Hesse矩阵相似的正定矩阵，这个构造方法，使用了目标函数的梯度（一阶导数）信息和两个点的“位移”（X_k-X_k-1）来实现。有人会说，是不是用Hesse矩阵的近似矩阵来代替Hesse矩阵，会导致求解效果变差呢？事实上，效果反而通常会变好。

拟牛顿法与牛顿法的迭代过程一样，仅仅是各个Hesse矩阵的求解方法不一样。

在远离极小值点处，Hesse矩阵一般不能保证正定，使得目标函数值不降反升。而拟牛顿法可以使目标函数值沿下降方向走下去，并且到了最后，在极小值点附近，可使构造出来的矩阵与Hesse矩阵“很像”了，这样，拟牛顿法也会具有牛顿法的二阶收敛性。

对目标函数f(X)做二阶泰勒展开：

两边对X求导

当X=X_i时，有

这里我们用H_i来代表在点X_i处的Hesse矩阵的逆，则

(5)式就是拟牛顿方程。

下面给出拟牛顿法中的一种--DFP法。

令

我们希望H_i+1在H_i的基础上加一个修正来得到：

给定E_i的一种形式：

m和n均为实数，v和w均为N维向量。

(6)(7)联合起来代入(5)可得：

下面再给一种拟牛顿法--BFGS算法。

 

(8)式中黑色的部分就是DFP算法，红色部分是BFGS比DFP多出来的部分。

BFGS算法不仅具有二次收敛性，而且只有初始矩阵对称正定，则BFGS修正公式所产生的矩阵H_k也是对称正定的，且H_k不易变为奇异，因此BFGS比DFP具有更好的数值稳定性。

共轭方向法

最速下降法有锯齿现像，收敛速度慢；而牛顿法需要计算Hesse矩阵而计算量大。共轭方向法收敛速度界于两者之间，具有二次收敛性。共轭方向法属于效果好而又实用的方法。

由于一般目标函数在最优点附近呈现为二次函数，因此可以设想一个算法对于二次函数比较有效，就可能对一般函数也有较好效果。共轭方向法是在研究对称正定二次函数的基础上提出来的。

则称两个向量P₀和P₁为Q的共轭向量。当Q为单位向量时，有，所以“共轭”是“正交”的推广。

对于二次正定函数，从任意点X⁰出发，沿任意下降方向P⁰作直线搜索得到X¹，再从X¹出发，沿与P⁰共轭的方向P¹作直线搜索，即可得到f(X)的极小点。

当一组向量Pⁱ（i=1,2,...,n-1）为Q共轭时，从任意点出发，依次沿P⁰,P¹,P²,...,P^n-1方向作下述算法的直线搜索，经过n次迭代必定收敛于正定二次函数的极小点。

为确定最优步长t_k,令

现在问题是如何产生一组关于Q共轭的向量？这里一种叫作Gram-Schmidt的方法。

取线性无关的向量组V⁰,V¹,...,V^n-1，例如取n个坐标轴的单位向量。

取P⁰=V⁰.

上面的方法都是针对目标函数为正定二次函数的，对于一般非二次函数，可以通过二次近似。

这就是f(X)在极小点X*处的近似，是Hesse矩阵，相当于Q，由于X*未知，但当X⁰充分接近于X*时，可用近似代替，从而构造共轭向量。

理论与实践证明，将二次收敛算法用于非二次的目标函数，亦有很好的效果，但迭代次数不一定保证有限次，即对非二次n维目标函数经n步共轭方向一维搜索不一定就能达到极小点。在这种情况下，为了找到极小点，可用泰勒级数将该函数在极小点附近展开，略去高于二次的项之后即可得该函数的二次近似。实际上很多的函数都可以用二次函数很好地近似，甚至在离极小点不是很近的点也是这样。故用二次函数近似代替非二次函数来处理的方法不仅在理论分析上是重要的，而且在工程实际应用中也是可取的。

共轭梯度法

共轭梯度法是共轭方向法的一种延伸，初始共轭向量P⁰由初始迭代点X⁰处的负梯度-g⁰来给出。以后的P^k由当前迭代点的负梯度与上一个共轭向量的线性组合来确定：

对于非二次函数的优化问题，迭代次数不止n次，但共轭方向只有n个。当迭代n次后，可以把Pⁿ重新置为最开始的P⁰，其他的变量按原方法更新。