0019算法笔记——【动态规划】0-1背包问题
1、问题描述：
给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大?
形式化描述：给定c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最大.即一个特殊的整数规划问题。
2、最优性原理：
设(y1,y2,…,yn)是 (3.4.1)的一个最优解.则(y2,…,yn)是下面相应子问题的一个最优解:
证明:使用反证法。若不然,设(z2,z3,…,zn)是上述子问题的一个最优解,而(y2,y3,…,yn)不是它的最优解。显然有
∑vizi > ∑viyi (i=2,…,n)
且 w1y1+ ∑wizi<= c
因此 v1y1+ ∑vizi (i=2,…,n) > ∑ viyi, (i=1,…,n)
说明(y1,z2, z3,…,zn)是(3.4.1)0-1背包问题的一个更优解,导出(y1,y2,…,yn)不是背包问题的最优解,矛盾。
3、递推关系：
设所给0-1背包问题的子问题
的最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质，可以建立计算m(i，j)的递归式:
注:(3.4.3)式此时背包容量为j，可选择物品为i。此时在对xi作出决策之后,问题处于两种状态之一:
(1)背包剩余容量是j,没产生任何效益；
(2)剩余容量j-wi,效益值增长了vi ；
算法具体代码如下：
- //3d10-1 动态规划 背包问题
- #include "stdafx.h"
- #include <iostream>
- using namespace std;
- const int N = 4;
- void Knapsack(int v[],int w[],int c,int n,int m[][10]);
- void Traceback(int m[][10],int w[],int c,int n,int x[]);
- int main()
- {
- int c=8;
- int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始
- int x[N+1];
- int m[10][10];
- cout<<"待装物品重量分别为："<<endl;
- for(int i=1; i<=N; i++)
- {
- cout<<w[i]<<" ";
- }
- cout<<endl;
- cout<<"待装物品价值分别为："<<endl;
- for(int i=1; i<=N; i++)
- {
- cout<<v[i]<<" ";
- }
- cout<<endl;
- Knapsack(v,w,c,N,m);
- cout<<"背包能装的最大价值为："<<m[1][c]<<endl;
- Traceback(m,w,c,N,x);
- cout<<"背包装下的物品编号为："<<endl;
- for(int i=1; i<=N; i++)
- {
- if(x[i]==1)
- {
- cout<<i<<" ";
- }
- }
- cout<<endl;
- return 0;
- }
- void Knapsack(int v[],int w[],int c,int n,int m[][10])
- {
- int jMax = min(w[n]-1,c);//背包剩余容量上限 范围[0~w[n]-1]
- for(int j=0; j<=jMax;j++)
- {
- m[n][j]=0;
- }
- for(int j=w[n]; j<=c; j++)//限制范围[w[n]~c]
- {
- m[n][j] = v[n];
- }
- for(int i=n-1; i>1; i--)
- {
- jMax = min(w[i]-1,c);
- for(int j=0; j<=jMax; j++)//背包不同剩余容量j<=jMax<c
- {
- m[i][j] = m[i+1][j];//没产生任何效益
- }
- for(int j=w[i]; j<=c; j++) //背包不同剩余容量j-wi >c
- {
- m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);//效益值增长vi
- }
- }
- m[1][c] = m[2][c];
- if(c>=w[1])
- {
- m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);
- }
- }
- //x[]数组存储对应物品0-1向量,0不装入背包，1表示装入背包
- void Traceback(int m[][10],int w[],int c,int n,int x[])
- {
- for(int i=1; i<n; i++)
- {
- if(m[i][c] == m[i+1][c])
- {
- x[i]=0;
- }
- else
- {
- x[i]=1;
- c-=w[i];
- }
- }
- x[n]=(m[n][c])?1:0;
- }
//3d10-1 动态规划 背包问题
#include "stdafx.h"
#include <iostream>
using namespace std;
const int N = 4;
void Knapsack(int v[],int w[],int c,int n,int m[][10]);
void Traceback(int m[][10],int w[],int c,int n,int x[]);
int main()
{
int c=8;
int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始
int x[N+1];
int m[10][10];
cout<<"待装物品重量分别为："<<endl;
for(int i=1; i<=N; i++)
{
cout<<w[i]<<" ";
}
cout<<endl;
cout<<"待装物品价值分别为："<<endl;
for(int i=1; i<=N; i++)
{
cout<<v[i]<<" ";
}
cout<<endl;
Knapsack(v,w,c,N,m);
cout<<"背包能装的最大价值为："<<m[1][c]<<endl;
Traceback(m,w,c,N,x);
cout<<"背包装下的物品编号为："<<endl;
for(int i=1; i<=N; i++)
{
if(x[i]==1)
{
cout<<i<<" ";
}
}
cout<<endl;
return 0;
}
void Knapsack(int v[],int w[],int c,int n,int m[][10])
{
int jMax = min(w[n]-1,c);//背包剩余容量上限 范围[0~w[n]-1]
for(int j=0; j<=jMax;j++)
{
m[n][j]=0;
}
for(int j=w[n]; j<=c; j++)//限制范围[w[n]~c]
{
m[n][j] = v[n];
}
for(int i=n-1; i>1; i--)
{
jMax = min(w[i]-1,c);
for(int j=0; j<=jMax; j++)//背包不同剩余容量j<=jMax<c
{
m[i][j] = m[i+1][j];//没产生任何效益
}
for(int j=w[i]; j<=c; j++) //背包不同剩余容量j-wi >c
{
m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);//效益值增长vi
}
}
m[1][c] = m[2][c];
if(c>=w[1])
{
m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);
}
}
//x[]数组存储对应物品0-1向量,0不装入背包，1表示装入背包
void Traceback(int m[][10],int w[],int c,int n,int x[])
{
for(int i=1; i<n; i++)
{
if(m[i][c] == m[i+1][c])
{
x[i]=0;
}
else
{
x[i]=1;
c-=w[i];
}
}
x[n]=(m[n][c])?1:0;
}
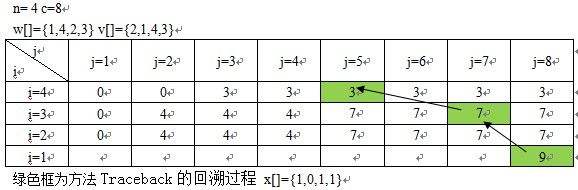
算法执行过程对m[][]填表及Traceback回溯过程如图所示：
从m(i，j)的递归式容易看出，算法Knapsack需要O(nc)计算时间; Traceback需O(n)计算时间；算法总体需要O(nc)计算时间。当背包容量c很大时，算法需要的计算时间较多。例如，当c>2^n时，算法需要Ω(n2^n)计算时间。
4、算法的改进：
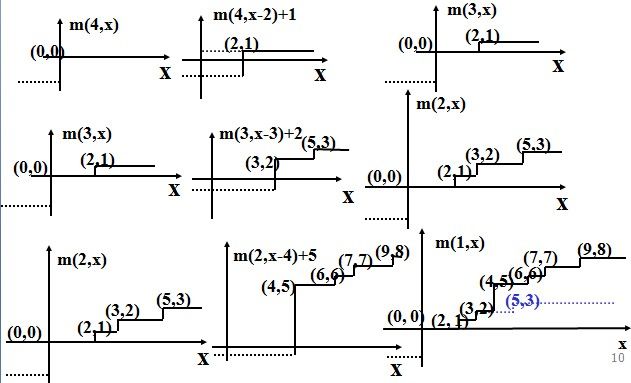
由m(i,j)的递归式容易证明，在一般情况下，对每一个确定的i(1≤i≤n)，函数m(i,j)是关于变量j的阶梯状单调不减函数。跳跃点是这一类函数的描述特征。在一般情况下，函数m(i,j)由其全部跳跃点唯一确定。如图所示。
对每一个确定的i(1≤i≤n)，用一个表p[i]存储函数m(i，j)的全部跳跃点。表p[i]可依计算m(i，j)的递归式递归地由表p[i+1]计算，初始时p[n+1]={(0，0)}。
一个例子：n=3，c=6，w={4，3，2}，v={5，2，1}。
函数m(i,j)是由函数m(i+1,j)与函数m(i+1,j-wi)+vi作max运算得到的。因此，函数m(i,j)的全部跳跃点包含于函数m(i+1，j)的跳跃点集p[i+1]与函数m(i+1，j-wi)+vi的跳跃点集q[i+1]的并集中。易知，(s,t)∈q[i+1]当且仅当wi<=s<=c且(s-wi,t-vi)∈p[i+1]。因此，容易由p[i+1]确定跳跃点集q[i+1]如下：
q[i+1]=p[i+1]⊕(wi,vi)={(j+wi,m(i,j)+vi)|(j,m(i,j))∈p[i+1]}
另一方面，设(a，b)和(c，d)是p[i+1]∪q[i+1]中的2个跳跃点，则当c>=a且d<b时，(c，d)受控于(a，b)，从而(c，d)不是p[i]中的跳跃点。除受控跳跃点外，p[i+1]∪q[i+1]中的其他跳跃点均为p[i]中的跳跃点。
由此可见，在递归地由表p[i+1]计算表p[i]时，可先由p[i+1]计算出q[i+1]，然后合并表p[i+1]和表q[i+1]，并清除其中的受控跳跃点得到表p[i]。
例：n=5，c=10，w={2，2，6，5，4}，v={6，3，5，4，6}。跳跃点的计算过程如下：
初始时p[6]={(0,0)}，(w5,v5)=(4,6)。因此，q[6]=p[6]⊕(w5,v5)={(4,6)}。 p[5]={(0,0),(4,6)}。q[5]=p[5]⊕(w4,v4)={(5,4),(9,10)}。从跳跃点集p[5]与q[5]的并集p[5]∪q[5]={(0,0),(4,6),(5,4),(9,10)}中看到跳跃点(5,4)受控于跳跃点(4,6)。将受控跳跃点(5,4)清除后，得到
p[4]={(0,0),(4,6),(9,10)}
q[4]=p[4]⊕(6，5)={(6，5)，(10，11)}
p[3]={(0，0)，(4，6)，(9，10)，(10，11)}
q[3]=p[3]⊕(2，3)={(2，3)，(6，9)}
p[2]={(0，0)，(2，3)，(4，6)，(6，9)，(9，10)，(10，11)}
q[2]=p[2]⊕(2，6)={(2，6)，(4，9)，(6，12)，(8，15)}
p[1]={(0，0)，(2，6)，(4，9)，(6，12)，(8，15)}
p[1]的最后的那个跳跃点(8,15)给出所求的最优值为m(1,c)=15。
具体代码实现如下：
- //3d10-2 动态规划 背包问题 跳跃点优化
- #include "stdafx.h"
- #include <iostream>
- using namespace std;
- const int N = 4;
- template<class Type>
- int Knapsack(int n,Type c,Type v[],Type w[],int **p,int x[]);
- template<class Type>
- void Traceback(int n,Type w[],Type v[],Type **p,int *head,int x[]);
- int main()
- {
- int c=8;
- int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始
- int x[N+1];
- int **p = new int *[50];
- for(int i=0;i<50;i++)
- {
- p[i] = new int[2];
- }
- cout<<"待装物品重量分别为："<<endl;
- for(int i=1; i<=N; i++)
- {
- cout<<w[i]<<" ";
- }
- cout<<endl;
- cout<<"待装物品价值分别为："<<endl;
- for(int i=1; i<=N; i++)
- {
- cout<<v[i]<<" ";
- }
- cout<<endl;
- cout<<"背包能装的最大价值为："<<Knapsack(N,c,v,w,p,x)<<endl;
- cout<<"背包装下的物品编号为："<<endl;
- for(int i=1; i<=N; i++)
- {
- if(x[i]==1)
- {
- cout<<i<<" ";
- }
- }
- cout<<endl;
- for(int i=0;i<50;i++)
- {
- delete p[i];
- }
- delete[] p;
- return 0;
- }
- template<class Type>
- int Knapsack(int n,Type c,Type v[],Type w[],int **p,int x[])
- {
- int *head = new int[n+2];
- head[n+1]=0;
- p[0][0]=0;//p[][0]存储物品重量
- p[0][1]=0;//p[][1]存储物品价值，物品n的跳跃点（0，0）
- // left 指向p[i+1]的第一个跳跃点，right指向最后一个
- //拿书上的例子来说，若计算p[3]=0;则left指向p[4]的第一跳跃点（0 0）right指向（9,10）
- int left = 0,right = 0,next = 1;//next即下一个跳跃点要存放的位置
- head[n]=1;//head[n]用来指向第n个物品第一个跳跃点的位置
- for(int i=n; i>=1; i--)
- {
- int k = left;//k指向p[ ]中跳跃点,移动k来判断p[]与p[]+（w v）中的受控点
- for(int j=left; j<=right; j++)
- {
- if(p[j][0]+w[i]>c) break;//剩余的空间不能再装入i，退出for循环;
- Type y = p[j][0] + w[i],m = p[j][1] + v[i];//计算p[ ]+（w v）
- //若p[k][0]较小则(p[k][0] p[k][1])一定不是受控点，将其作为p[i]的跳跃点存储
- while(k<=right && p[k][0]<y)
- {
- p[next][0]=p[k][0];
- p[next++][1]=p[k++][1];
- }
- //如果 p[k][0]==y而m<p[k][1]，则（y m）为受控点不存
- if(k<=right && p[k][0]==y)
- {
- if(m<p[k][1])//对（p[k][0] p[k][1]）进行判断
- {
- m=p[k][1];
- }
- k++;
- }
- // 若p[k][0]>=y且m> =p[k][1],判断是不是当前i的最后一个跳跃点的受控点
- //若不是则为i的跳跃点存储
- if(m>p[next-1][1])
- {
- p[next][0]=y;
- p[next++][1]=m;
- }
- //若是，则对下一个元素进行判断。
- while(k<=right && p[k][1]<=p[next-1][1])
- {
- k++;
- }
- }
- while(k<=right)
- {
- p[next][0]=p[k][0];
- p[next++][1]=p[k++][1];//将i+1剩下的跳跃点作为做为i的跳跃点存储
- }
- left = right + 1;
- right = next - 1;
- // 第i-1个物品第一个跳跃点的位置 head[0]指第0个物品第一个跳跃点的位置
- head[i-1] = next;
- }
- Traceback(n,w,v,p,head,x);
- return p[next-1][1];
- }
- //x[]数组存储对应物品0-1向量,0不装入背包，1表示装入背包
- template<class Type>
- void Traceback(int n,Type w[],Type v[],Type **p,int *head,int x[])
- {
- //初始化j,m为最后一个跳跃点对应的第0列及第1列
- //如上例求出的 最后一个跳跃点为（8 15）j=8,m=15
- Type j = p[head[0]-1][0],m=p[head[0]-1][1];
- for(int i=1; i<=n; i++)
- {
- x[i]=0;// 初始化数组；
- for(int k=head[i+1]; k<=head[i]-1;k++)// 初始k指向p[2]的第一个跳跃点（0 0）
- {
- //判断物品i是否装入，如上例与跳跃点(6 9)相加等于（8 15）所以1装入
- if(p[k][0]+w[i]==j && p[k][1]+v[i]==m)
- {
- x[i]=1;//物品i被装入，则x[i]置1
- j=p[k][0];// j和m值置为满足if条件的跳跃点对应的值
- m=p[k][1];// 如上例j=6,m=9
- break;//再接着判断下一个物品
- }
- }
- }
- }
//3d10-2 动态规划 背包问题 跳跃点优化
#include "stdafx.h"
#include <iostream>
using namespace std;
const int N = 4;
template<class Type>
int Knapsack(int n,Type c,Type v[],Type w[],int **p,int x[]);
template<class Type>
void Traceback(int n,Type w[],Type v[],Type **p,int *head,int x[]);
int main()
{
int c=8;
int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始
int x[N+1];
int **p = new int *[50];
for(int i=0;i<50;i++)
{
p[i] = new int[2];
}
cout<<"待装物品重量分别为："<<endl;
for(int i=1; i<=N; i++)
{
cout<<w[i]<<" ";
}
cout<<endl;
cout<<"待装物品价值分别为："<<endl;
for(int i=1; i<=N; i++)
{
cout<<v[i]<<" ";
}
cout<<endl;
cout<<"背包能装的最大价值为："<<Knapsack(N,c,v,w,p,x)<<endl;
cout<<"背包装下的物品编号为："<<endl;
for(int i=1; i<=N; i++)
{
if(x[i]==1)
{
cout<<i<<" ";
}
}
cout<<endl;
for(int i=0;i<50;i++)
{
delete p[i];
}
delete[] p;
return 0;
}
template<class Type>
int Knapsack(int n,Type c,Type v[],Type w[],int **p,int x[])
{
int *head = new int[n+2];
head[n+1]=0;
p[0][0]=0;//p[][0]存储物品重量
p[0][1]=0;//p[][1]存储物品价值，物品n的跳跃点（0，0）
// left 指向p[i+1]的第一个跳跃点，right指向最后一个
//拿书上的例子来说，若计算p[3]=0;则left指向p[4]的第一跳跃点（0 0）right指向（9,10）
int left = 0,right = 0,next = 1;//next即下一个跳跃点要存放的位置
head[n]=1;//head[n]用来指向第n个物品第一个跳跃点的位置
for(int i=n; i>=1; i--)
{
int k = left;//k指向p[ ]中跳跃点,移动k来判断p[]与p[]+（w v）中的受控点
for(int j=left; j<=right; j++)
{
if(p[j][0]+w[i]>c) break;//剩余的空间不能再装入i，退出for循环;
Type y = p[j][0] + w[i],m = p[j][1] + v[i];//计算p[ ]+（w v）
//若p[k][0]较小则(p[k][0] p[k][1])一定不是受控点，将其作为p[i]的跳跃点存储
while(k<=right && p[k][0]<y)
{
p[next][0]=p[k][0];
p[next++][1]=p[k++][1];
}
//如果 p[k][0]==y而m<p[k][1]，则（y m）为受控点不存
if(k<=right && p[k][0]==y)
{
if(m<p[k][1])//对（p[k][0] p[k][1]）进行判断
{
m=p[k][1];
}
k++;
}
// 若p[k][0]>=y且m> =p[k][1],判断是不是当前i的最后一个跳跃点的受控点
//若不是则为i的跳跃点存储
if(m>p[next-1][1])
{
p[next][0]=y;
p[next++][1]=m;
}
//若是，则对下一个元素进行判断。
while(k<=right && p[k][1]<=p[next-1][1])
{
k++;
}
}
while(k<=right)
{
p[next][0]=p[k][0];
p[next++][1]=p[k++][1];//将i+1剩下的跳跃点作为做为i的跳跃点存储
}
left = right + 1;
right = next - 1;
// 第i-1个物品第一个跳跃点的位置 head[0]指第0个物品第一个跳跃点的位置
head[i-1] = next;
}
Traceback(n,w,v,p,head,x);
return p[next-1][1];
}
//x[]数组存储对应物品0-1向量,0不装入背包，1表示装入背包
template<class Type>
void Traceback(int n,Type w[],Type v[],Type **p,int *head,int x[])
{
//初始化j,m为最后一个跳跃点对应的第0列及第1列
//如上例求出的 最后一个跳跃点为（8 15）j=8,m=15
Type j = p[head[0]-1][0],m=p[head[0]-1][1];
for(int i=1; i<=n; i++)
{
x[i]=0;// 初始化数组；
for(int k=head[i+1]; k<=head[i]-1;k++)// 初始k指向p[2]的第一个跳跃点（0 0）
{
//判断物品i是否装入，如上例与跳跃点(6 9)相加等于（8 15）所以1装入
if(p[k][0]+w[i]==j && p[k][1]+v[i]==m)
{
x[i]=1;//物品i被装入，则x[i]置1
j=p[k][0];// j和m值置为满足if条件的跳跃点对应的值
m=p[k][1];// 如上例j=6,m=9
break;//再接着判断下一个物品
}
}
}
}
上述算法的主要计算量在于计算跳跃点集p[i](1≤i≤n)。由于q[i+1]=p[i+1]⊕(wi，vi)，故计算q[i+1]需要O(|p[i+1]|)计算时间。合并p[i+1]和q[i+1]并清除受控跳跃点也需要O(|p[i+1]|)计算时间。从跳跃点集p[i]的定义可以看出，p[i]中的跳跃点相应于xi,…,xn的0/1赋值。因此，p[i]中跳跃点个数不超过2^(n-i+1)。由此可见，算法计算跳跃点集p[i]所花费的计算时间为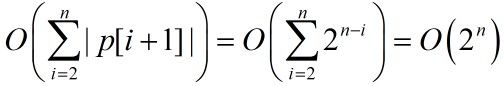
从而，改进后算法的计算时间复杂性为O(2^n)。当所给物品的重量wi(1≤i≤n)是整数时，|p[i]|≤c+1，(1≤i≤n)。在这种情况下，改进后算法的计算时间复杂性为O(min{nc,2^n})。
运行结果如图：
