【BZOJ1185】最小矩形覆盖 计算几何 凸包 旋转卡壳
写完程序两小时,调对精度一小时hhh
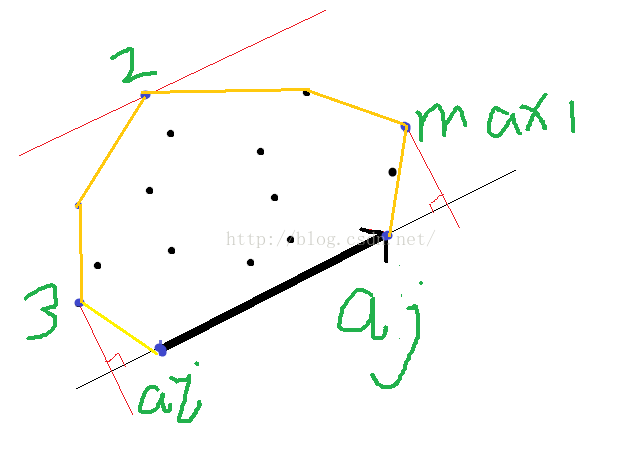
首先不严格的直觉告诉我们所求矩形一定有一条边在凸包上,我们遍历凸包上的边,用类似旋转卡壳的方式得到凸包上的三个点,分别是在边上投影最靠前的点,在边上投影最靠后的点,距离边最远的点 ,这三个点一定在所求矩形的另外三条边上。得到一个矩形求解即可。
我尽力了。。。
判断1号点和2号点时要同时运用内积(点乘)和外积(叉乘)与0的大小关系,具体见代码
/**************************************************************
Problem: 1185
User: RicardoWang
Language: C++
Result: Accepted
Time:236 ms
Memory:2840 kb
****************************************************************/
#include<cstdlib>
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
#define maxn 50005
double eps=1e-8;
double fabs(double x)
{
return x<0 ?-x:x;
}
struct P
{
double x,y;
P(double x=0,double y=0) : x(x),y(y) {}
}A[maxn],s[maxn];
double operator * (P x,P y)
{
return x.x*y.y-x.y*y.x;
}
P operator - (P x,P y)
{
return P(x.x-y.x,x.y-y.y);
}
double dis(P x,P y)
{
return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));
}
bool operator < (P x,P y)
{
double t=(x-A[1])*(y-A[1]);
if(t==0)return dis(x,A[1])<dis(y,A[1]);
else return t>0;
}
int n,top;
void Init()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf",&A[i].x,&A[i].y);
}
return ;
}
void graham()
{
int k=1;
for(int i=1;i<=n;i++)if(A[i].x<A[k].x ||(A[i].x == A[k].x && A[i].y<A[k].y))k=i;
if(k!=1)swap(A[k],A[1]);
sort(A+2,A+1+n);
s[++top]=A[1];
for(int i=2;i<=n;i++)
{
while(top>1 && (s[top]-s[top-1])*(A[i]-s[top])<=eps)top--;
s[++top]=A[i];
}
for(int i=1;i<=top;i++)
{
// printf("%.5lf %.5lf\n",s[i].x,s[i].y);
}
return ;
}
struct line
{
double A,B,C;
void get(P x,P y)
{
if(fabs(x.x-y.x)<=eps)
{
A=1; B=0; C=-x.x;
}
else
{
A=(y.y-x.y)/(y.x-x.x); B=-1; C=-A*x.x-B*x.y;
}
return ;
}
void getdx(P x,P y)
{
A=y.x; B=y.y; C=-A*x.x-B*x.y;
}
}S[5];
P ans[5],t[5];
P operator * (line x,line y)
{
P ans;
double f,X,Y;
if(fabs(y.B)<=eps)
{
X=(-y.C/y.A); Y=(x.A*X+x.C)/(-x.B);
}
else
{
f=-x.B/y.B; X=-(x.C+f*y.C)/(x.A+f*y.A); Y=(y.A*X+y.C)/(-y.B);
}
return P (X,Y);
}
double Sum=-1;
void getS(int A,int B,int x,int y,int z)
{
P vec=s[B]-s[A];
S[1].get(s[A],s[B]);
S[2].getdx(s[x],vec);
S[3].getdx(s[y],P(vec.y,-vec.x));
S[4].getdx(s[z],vec);
P c[5];
for(int i=1;i<=4;i++)c[i]=S[i]*S[i%4+1];
double ss=(c[2]-c[1])*(c[4]-c[1]);if(ss<0)ss=-ss;
if(ss<Sum || Sum==-1)
{
Sum=ss;
for(int i=1;i<=4;i++)ans[i]=c[i];
}
return ;
}
double dian(P x,P y)
{
return x.x*y.x+x.y*y.y;
}
void work()
{
int max1=2,max2=2,max3=2,j;
for(int i=1;i<=top;i++)
{
j=i%top+1;
while (max1%top+1!=i && !((s[max1%top+1]-s[max1])*(s[j]-s[i])<=0 && dian((s[max1%top+1]-s[max1]),s[j]-s[i])<=0 ))max1=max1%top+1;
while (max3%top+1!=i && !((s[max3%top+1]-s[max3])*(s[j]-s[i])>=0 && dian((s[max3%top+1]-s[max3]),s[j]-s[i])>=0 ))max3=max3%top+1;
while (max2%top+1!=i && (s[j]-s[i])*(s[max2%top+1]-s[max2])>=0 )max2=max2%top+1;
getS(i,j,max1,max2,max3);
}
int first=1;
for(int i=2;i<=4;i++)if((fabs(ans[i].y-ans[first].y)>eps && ans[i].y<ans[first].y) || (fabs(ans[i].y-ans[first].y)<=eps && ans[i].x<ans[first].x))first=i;
printf("%.5lf\n",Sum);
for(int i=1;i<=4;i++)
{
if(fabs(ans[i].x)<=eps)ans[i].x=0;
if(fabs(ans[i].y)<=eps)ans[i].y=0;
}
for(int i=1;i<=4;i++)
{printf("%.5lf %.5lf\n",ans[first].x,ans[first].y);first=first%4+1;}
return ;
}
int main()
{
// freopen("in.txt","r",stdin);
Init();
graham();
work();
return 0;
}