从头到尾理解KMP算法
从头到尾理解KMP算法
KMP算法解决的问题是字符匹配,是由Knuth–Morris–Pratt共同开发出来的,这个算法把字符匹配的时间复杂度缩小到O(m+n),而空间复杂度也只有O(m),n是target的长度,m是pattern的长度,在此算法在发明之前并不是没有如此高效的算法,但是原算法比较复杂。Kmp算法优雅高效,但是实现却不难理解且代码长度很短,是优秀算法设计的典范,值得拿出来仔细分析。< xmlnamespace prefix ="o" ns ="urn:schemas-microsoft-com:office:office" />
一、原始匹配算法
并先来看一个比较原始的匹配算法,对于目的字串target是banananobano,要匹配的字串pattern是nano,的情况,下面是匹配过程,原理很简单,只要先和target字串的第一个字符比较,如果相同就比较下一个,如果不同就把pattern右移一下,之后再从pattern的每一个字符比较,这个算法的运行过程如下图,index表示的每n次匹配的情形,这种匹配的代码也比较容易写,如下面:
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
| b |
a |
n |
a |
n |
a |
n |
o |
b |
a |
n |
o |
|
| index=0 |
X |
|||||||||||
| index=1 |
X |
|||||||||||
| index=2 |
n |
a |
n |
X |
||||||||
| index=3 |
X |
|||||||||||
| index=4 |
n |
a |
n |
o |
||||||||
| index=5 |
X |
|||||||||||
| index=6 |
n |
X |
||||||||||
| index=7 |
X |
|||||||||||
| index=8 |
X |
|||||||||||
| index=9 |
X |
|||||||||||
| index=10 |
n |
X |
||||||||||
| index=11 |
X |
#include<iostream>
#include<string>
using namespace std;
int match(const string& target,const string& pattern)
{
int target_length = target.size();
int pattern_length = pattern.size();
int target_index = 0;
int pattern_index = 0;
while(target_index < target_length && pattern_index < pattern_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else
{
target_index -= (pattern_index-1);
pattern_index = 0;
}
}
if(pattern_index = pattern_length)
{
return target_index - pattern_length;
}
else
{
return -1;
}
}
int main()
{
cout<<match("banananobano","nano")<<endl;
return 0;
}
上面的算法进间复杂度是O(pattern_length*target_length),我们主要把时间浪费在什么地方呢,观查index =2那一步,我们已经匹配了3个字符,而第4个字符是不匹配的,这时我们已经匹配的字符序列是nan, 此时如果向右移动一位,那么nan最先匹配的字符序列将是an,这肯定是不能匹配的,之后再右移一位,匹配的是nan最先匹配的序列是n,这是可以匹配的,如果我们事先知道pattern本身的这些信息就不用每次匹配失败后都把target_index回退回去,这种回退就浪费了很多不必要的时间,如果能事先计算出pattern本身的这些性质,那么就可以在失配时直接把pattern移动到下一个可能的位置,把其中根本不可能匹配的过程省略掉,如上表所示我们在index=2时失配,此时就可以直接把pattern移动到index=4的状态,kmp算法就是从此出发。
二、kmp算法
1. 覆盖函数(overlay_function)
覆盖函数所表征的是pattern本身的性质,可以让为其表征的是pattern从左开始的所有连续子串的自我覆盖程度。
比如如下的字串,abaabcaba
| 子串 |
值 |
| a |
-1 |
| ab |
-1 |
| aba |
0 |
| abaa |
0 |
| abaab |
1 |
| abaabc |
-1 |
| abaabca |
0 |
| abaabcab |
1 |
| abaabcaba |
2 |
于由计数是从0始的,因此覆盖函数的值为0说明有1个匹配,对于从0还是从来开始计数是偏好问题,具体请自行调整,其中-1表示没有覆盖,那么何为覆盖呢,下面比较数学的来看一下定义,比如对于序列
我样要找到一个k,使它满足前
而没有更大的k满足这个条件,就是说要找到尽可能大k,使pattern前k字符与后k字符相匹配,k要尽可能的大,原因是如果有比较大的k存在,而我们选择较小的满足条件的k,那么当失配时,我们就会使pattern向右移动的位置变大,而较少的移动位置是存在匹配的,这样我们就会把可能匹配的结果丢失。比如下面的序列,
| target |
a |
a |
b |
c |
a |
a |
x |
d |
n |
f |
d |
| pattern |
a |
a |
b |
c |
a |
a |
n |
||||
| k=1 |
a |
a |
b |
c |
a |
a |
|||||
| k=0 |
a |
a |
b |
c |
a |
a |
在红色部分失配,正确的结果是k=1的情况,把pattern右移4位,如果选择k=0,右移5位则会产生错误。
计算这个overlay函数的方法可以采用递推,可以想象如果对于pattern的前j个字符,如果覆盖函数值为k
则对于pattern的前j+1序列字符,则有如下可能
⑴ pattern[k+1]==pattern[j+1] 此时overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此时只能在pattern前k+1个子符组所的子串中找到相应的overlay函数,h=overlay(k),如果此时pattern[h+1]==pattern[j+1],则overlay(j+1)=h+1否则重复(2)过程.
下面给出一种计算覆盖的代码
#include<iostream>
#include<string>
using namespace std;
void compute_overlay(const string& pattern)
{
const int pattern_length = pattern.size();
int *overlay_function = new int[pattern_length];
int index;
overlay_function[0] = -1;
for(int i=1;i<pattern_length;++i)
{
index = overlay_function[i-1];
//store previous fail position k to index;
while(index>=0 && pattern[i]!=pattern[index+1])
{
index = overlay_function[index];
}
if(pattern[i]==pattern[index+1])
{
overlay_function[i] = index + 1;
}
else
{
overlay_function[i] = -1;
}
}
for(int i=0;i<pattern_length;++i)
{
cout<<overlay_function[i]<<endl;
}
delete[] overlay_function;
}
int main()
{
string pattern = "abaabcaba";
compute_overlay(pattern);
return 0;
}
2,kmp算法
有了覆盖函数,那么实现kmp算法就是很简单的了,我们的原则还是从左向右匹配,但是当失配发生时,我们不用把target_index向回移动,target_index前面已经匹配过的部分在pattern自身就能体现出来,只要动pattern_index就可以了,当发生在j长度失配时,只要把pattern向右移动j-overlay(j)长度就可以了,如果失配时pattern_index==0,相当于pattern第一个字符就不匹配,这时就应该把target_index加1,向右移动1位就可以了。
下面是具体实现的代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
{
const int target_length = target.size();
const int pattern_length = pattern.size();
int * overlay_value = new int[pattern_length];
overlay_value[0] = -1;
int index = 0;
for(int i=1;i<pattern_length;++i)
{
index = overlay_value[i-1];
while(index>=0 && pattern[index+1]!=pattern[i])
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
}
else
{
overlay_value[i] = -1;
}
}
//match algorithm start
int pattern_index = 0;
int target_index = 0;
while(pattern_index<pattern_length&&target_index<target_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else if(pattern_index==0)
{
++target_index;
}
else
{
pattern_index = overlay_value[pattern_index-1]+1;
}
}
if(pattern_index==pattern_length)
{
return target_index-pattern_index;
}
else
{
return -1;
}
delete [] overlay_value;
}
int main()
{
string source = " annbcdanacadsannannabnna";
string pattern = " annacanna";
cout<<kmp_find(source,pattern)<<endl;
return 0;
}
下面是kmp匹配过程序图
| 目标字串annbcdanacadsannannabnna 匹配模式annacanna |
|||||||||||||||||||||||||
| 移动序列 |
a |
n |
n |
b |
c |
d |
a |
n |
a |
c |
a |
d |
s |
a |
n |
n |
a |
n |
n |
a |
c |
a |
n |
n |
a |
| index=0 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=1 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=2 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=3 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=4 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=5 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=6 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=7 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=8 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=9 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=10 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=11 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=12 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=13 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=14 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=15 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
| index=16 |
a |
n |
n |
a |
c |
a |
n |
n |
a |
||||||||||||||||
图中黄色标注的行为通过overlay函数跳过的行,绿色为匹配序列,红色为失配位置。
三、kmp算法的来源
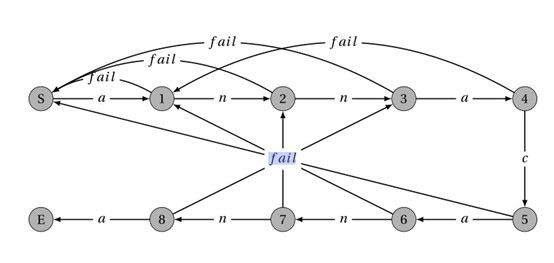
kmp如此精巧,那么它是怎么来的呢,为什么要三个人合力才能想出来。其实就算没有kmp算法,人们在字符匹配中也能找到相同高效的算法。这种算法,最终相当于kmp算法,只是这种算法的出发点不是覆盖函数,不是直接从匹配的内在原理出发,而使用此方法的计算的覆盖函数过程序复杂且不易被理解,但是一但找到这个覆盖函数,那以后使用同一pattern匹配时的效率就和kmp一样了,其实这种算法找到的函数不应叫做覆盖函数,因为在寻找过程中根本没有考虑是否覆盖的问题。说了这么半天那么这种方法是什么呢,这种方法是就大名鼎鼎的确定的有限自动机(Deterministic finite state automaton DFA),DFA可识别的文法是3型文法,又叫正规文法或是正则文法,既然可以识别正则文法,那么识别确定的字串肯定不是问题(确定字串是正则式的一个子集)。对于如何构造DFA,是有一个完整的算法,这里不做介绍了。在识别确定的字串时使用DFA实在是大材小用,DFA可以识别更加通用的正则表达式,而用通用的构建DFA的方法来识别确定的字串,那这个overhead就显得太大了。kmp算法的可贵之处是从字符匹配的问题本身特点出发,巧妙使用覆盖函数这一表征pattern自身特点的这一概念来快速直接生成识别字串的DFA,因此对于kmp这种算法,理解这种算法高中数学就可以了,但是如果想从无到有设计出这种算法是要求有比较深的数学功底的,下面是上面的pattern生成的DFA。
红色是失配时的state-conversion的方向。就写到这里,希望能对那些想理解kmp算法的人有些帮助。
下面再补一张比较学术的图