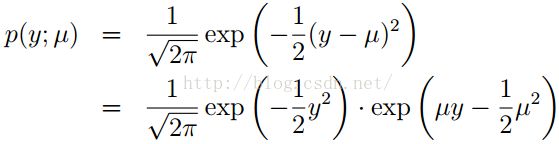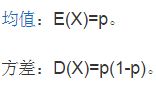MachineLearning—Logistic Regression(三)

  本篇博文为机器学习逻辑回归第三部分，主要介绍Generalized Linear Models(GLMs)广义线性模型；通过以前的学习我们发现无论是线性回归还是逻辑回归，无论是梯度上升亦或梯度下降它们在算法推导的过程当中都有非常近似的地方，通过这一部分的学习会发现有一根本的原因所决定：他们都属于指数家族函数集的某一特例。内容并不多，但可以通过这里对线性回归逻辑回归等部分有一个更为high level的理解，有问题欢迎一起交流(*^__^*) 嘻嘻……

符合这种形式的函数表达式我们称其为指数函数簇函数，确定T，a，b之后就确定了一个分布，我们可以通过改变η来获得不同的分布；下面我们通过推导来看一下高斯分布和伯努利分布其实都是指数函数簇的形式。

伯努利分布的联合分布律为：

其中η= log(φ/(1−φ))，我们可以将其转化为φ=1/(1 + e−η)这个式子比较重要，在后面的逻辑回归当中会用到；

我们发现当T，a，b取合适值时，伯努利分布可以写成为指数函数簇的形式；

下面我们再来看一下高斯分布：

回顾我们在推倒线性回归的时候会发现，δ2对我们最后的结果θ和h(x)没有任何的影响，所以我们索性为了方便将δ2=1；

我们发现当T，a，b取合适值时，高斯分布也是一种指数分布簇

其实还有很多其他分布函数，例如多项式，泊松，伽马，贝塔，狄利克雷等也都属于指数分布簇成员；

在构造广义线性模型之前我们约定了三条规则：

1、y |x;θ ∼指数分布簇

2、我们最终的目标是要使学习得到的h(x) = E[y|x]

3、η = θTx

有了这三条规则我们下面就可以证明逻辑回归和均方误差都可以通过GLM推导得出；

普通最小二乘法（Ordinary Least Squares）

我们把在给定x情况下的y条件分布假定为高斯分布，即 y~N (µ, σ2)

因为y服从高斯分布，也就是指数集分布，所以均方误差也是指数集的分布，也就是GLM。

逻辑回归（Logistic Regression）

首先伯努利分布的性质有：

作为一个二分类问题，我们很自然的联想到用伯努利分布来描述逻辑回归的条件分布，前面我们得出来一个很重要的公式是：

φ = 1/(1 + e−η) 而且 y|x;θ ∼ Bernoulli(φ), E[y|x; θ] = φ ，注意φ其实就是伯努利分布中的P

可以看出一旦我们假定了伯努利条件分布，我们就会得出GLM广义线性模型的结果，也就是指数分布函数簇的样子；