算法学习（3）分治策略（棋盘覆盖）

【问题描述】

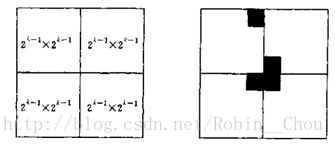
      在一个2^k×2^k个方格组成的棋盘中，有一个方格与其他方格不同，称该方格为一特殊方格，并称该棋盘为一个特殊棋盘。显然特殊方格在棋盘上出现的位置有4^k种情形。因而对任何k≥0,有4^k种不同的特殊棋盘。棋盘如图所示：

现在要求使用下面四种骨牌填充整个区域

【算法思路】

      先确定特殊方格的位置，也就是将大的棋牌分割成四块之后的哪一块里面。比如下图右中在左上边，那么久可以在分割方块的中间添加一个骨牌，这样分割后的四个区域都可以依次递归下去。

【代码实现】

#include <iostream>
#include <iomanip>

using namespace std;

//定义一个棋盘
int chess[8][8];
int tile = 1;

//tr:棋盘左上角的行号
//tc:棋盘左上角的列号
//dr:特殊方格的行号
//dc:特殊方格的列号
//size:棋盘的维数
void ChessCover(int tr,int tc,int dr,int dc,int size)
{
	if(size == 1) return;
	int t = tile++;		//骨牌编号
	int s = size / 2;	//分割棋盘
	//填补左上角
	if(dr < (tr+s) && dc < (tc+s))//特殊方格在左上角
		ChessCover(tr,tc,dr,dc,s);
	else//特殊方格不在左上角
	{
		chess[tr + s - 1][tc + s - 1] = t;
		ChessCover(tr,tc,tr+s-1,tc+s-1,s);
	}

	//填补右上角
	if(dr < (tr+s) && dc >= (tc+s))
		ChessCover(tr,tc+s,dr,dc,s);
	else
	{
		chess[tr + s - 1][tc + s] = t;
		ChessCover(tr,tc + s,tr + s - 1,tc + s,s);
	}


	//填补左下角
	if(dr >= (tr+s) && dc < (tc+s))
		ChessCover(tr+s,tc,dr,dc,s);
	else
	{
		chess[tr + s][tc + s - 1] = t;
		ChessCover(tr + s,tc,tr + s,tc + s - 1,s);
	}

	//填补右下角
	if(dr >= (tr+s) && dc >= (tc+s))
		ChessCover(tr+s,tc+s,dr,dc,s);
	else
	{
		chess[tr + s][tc + s] = t;
		ChessCover(tr + s,tc + s,tr + s,tc + s,s);
	}
}


int main()
{
	chess[2][2] = 0;//第一个棋子区
	ChessCover(0,0,2,2,8);
	for(int i = 0;i < 8;i++)
	{
		for(int j = 0;j < 8;j++)
			cout<<setw(3)<<chess[i][j];
		cout<<endl;
	}
	cout<<endl;
	system("pause");
	return 0;
}