卷积神经滤波CNN(一)
最近一直在研究卷积神经滤波(Convolutional Neural Networks)。看到Eric Yuan有一篇文章,写得不错,而国内中文的比较少,所以决定将其翻译过来。可能中间会有些自己的理解,如果有理解得不对的地方还希望大家多多指出。
一:卷积神经网络CNN
CNN实际上是由卷积层加标准的神经网络组成。CNN的结构是为了充分利用图像的2D结构而设计,它通过局部连接点和共享权值来实现。另一个CNN的优势是其易于训练,参数比相同隐层数的全连接网络要少很多。
卷积神经网络最先由Prof. Yann LeCun(NYU)发明。目前CNN对世界的产生了深厚的影响,每一个大IT公司都在对它进行研究。
二:主要思想
CNN简单来说就是将2D图像转到3D空间,这个转换由卷积实现。比如说:一张M*N大小的图像,使用k个m*n大小的卷积核,那么我们可以得到k*(M-m+1)*(N-n+1)图像。通过卷积,我们减少了图像的尺寸,却通过提升相邻像素的影像增加图像特征。更进一步,我们得到的卷积核实际上是通过训练得到的。在训练之后,我们可以看到生成的卷积核实际上像一些 Gabor滤波器。如果自己指定卷积核,那么不算是真的CNN。
2.1 卷积
卷积过程只是用中间有效部分,对于图像边缘卷积结果部分舍去。正如上文所说,一张M*N大小的图像,使用k个m*n大小的卷积核,那么我们可以得到k张(M-m+1)*(N-n+1)大小的图像。
2.2 Pooling(国内有人称是次抽样/亚采样)
这个图是一个典型的卷积神经网络结构图,其中的卷积层是对图像的一个邻域进行卷积得到图像的邻域特征,亚采样层就是使用pooling技术将小邻域内的特征点整合得到新的特征。
pooling的结果是使得特征减少,参数减少,但pooling的目的并不仅在于此。pooling目的是为了保持某种不变性(旋转、平移、伸缩等),常用的有mean-pooling,max-pooling和Stochastic-pooling三种。
mean-pooling,即对邻域内特征点只求平均,max-pooling,即对邻域内特征点取最大。根据相关理论,特征提取的误差主要来自两个方面:(1)邻域大小受限造成的估计值方差增大;(2)卷积层参数误差造成估计均值的偏移。一般来说,mean-pooling能减小第一种误差,更多的保留图像的背景信息,max-pooling能减小第二种误差,更多的保留纹理信息。Stochastic-pooling则介于两者之间,通过对像素点按照数值大小赋予概率,再按照概率进行亚采样,在平均意义上,与mean-pooling近似,在局部意义上,则服从max-pooling的准则。
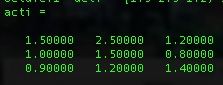
假设我们有以下的3*3的区域,我们想要获得Stochastic-pooling的次采样结果。
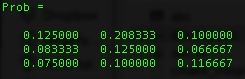
我们计算每个元素的可能性得到:
通过对可能性排序,我们得到:
现在我们随机选择一个0-8的数字,比如3,那么pooling的结果就是1.4.因为1.4的可能性排第四。你可能注意到我们所给的区域中有两个1.2,而两者的可能性都是0.1,,那么如果所给的随机数是4或者5,我们的选择就是1.2。这表明谁的可能性大谁就有更可能被选中。
当back-prop(后向传播)时,我们不改变选中的数字,其余的全部置零。如下图:
这和Max pooling的操作很相似。
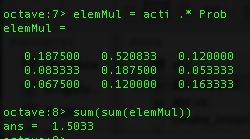
在编程时,我们只用简单地做一下矩阵相乘:
然后以1.5033为结果。
2.3 Back-prop(后向传播)
在这个部分和一般得神经网络并无差异,主要的差异在于前面的卷积和次采样。
2.4 Non-Linearity(非线性)
这个相对简单。一个非常流行的非线性函数是ReLU(Rectified Linear Unit),即
f(x) = max(0,x)
其导数也很简单
f`(x) = 1, x>0
f`(x) = 0,x<=0
原文地址 点击打开链接
参考 点击打开链接