线段树（一）

点修改&&区间修改的线段树。
线段树是一种数据结构，它能在log2n的时间完成一次操作。
没错它是一个非常犀利的数据结构。
也就是说，如果我们有n次操作，那么时间复杂度为O(nlog2n)。
而如果是暴力的算法，一定至少是O(n^2)。
而它的空间复杂度是O(4*n)，具体证明留(wo)给(zhen)读(de)者(bu)思(zhi)考(dao)。
线段树这种数据结构是用二叉树来储存的，而且是一个近似于完全二叉树的数据结构，
根据完全二叉树的性质，有当前节点(x)的左儿子编号为x<<1，右儿子编号为x<<1|1。
下图是一个线段树，不过它的下标是从0开始的，而我的写法是从1开始的。

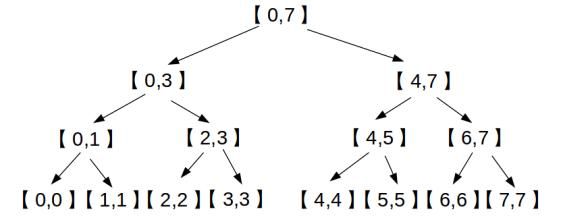
———————————-以下是构造——————————-
线段树是通过递归建立的，对它的操作也是需要递归实现。
线段树的建立跟二叉树的建立差不太多，而应用上面的性质，有当前节点(x)的左儿子编号为x<<1，右儿子编号为x<<1|1，从而建立出线段树。
Q：节点信息怎么办？
线段树中，某区间对应其子区间有一些关系，比方说我们想知道区间和，那么它的区间对应其子区间的关系就是：当前区间sum=左子区间sum+右子区间sum。
发现线段树好难讲……（划掉）
在构造完一棵线段树后，区间内元素只有一个的那些“极小区间”（叶子节点）就是题目中往往会给的初值啦~
而“极小区间”的父亲的信息是从“极小区间”获得的。
而“极小区间”的爷爷的信息是通过“极小区间”的父亲获得的。
—————————以下是修改———————————–
很好，我们讲完了构造，发现每个节点的信息如果要更改的话，比如说我如果想更改一个点的信息，那么只需要在l~r范围内进行查找，看这个点在l~mid 内还是在mid+1~r内即可，也就是我们查找的时间只需要log2n。而查找完了之后，由于我们是递归进行下去的，回溯时，会路过含有该区间信息的所有区间，到时候进行与构造线段树时相同获取信息的方法即可。（点修改，有一种牵一发而动全身的即视感（当然，有一些区间是没有路过的，所以勉强算是牵一发而动一下））
那区间修改呢？
误解：对每个区间内的每个点进行点修改。
正解：用一种叫做懒标记的东西，表明：该区间我将要进行修改。如果不对该区间询问，那么当前区间的懒标记永远不进行下传。
—————————以下是查询———————————–
你会发现实际上在建造整个线段树的过程中，如果你只需要单点查询，那么你只需要查询它的叶子节点即可，并且不需要知道所有非叶子节点区间的信息，而如果你需要区间查询，那么你需要记录所有区间的信息，也就意味着，如果你只需要单点查询，那么你就不需要获取非叶子节点的信息。
——然而你数组已经开了，还是获取一下信息吧，反正也节省不掉空间。（没错如果不写肯定节省时间）
查询似乎也讲的差不多了。
——————————————————————————
经典例(shui)题：
POJ 3468 A Simple Problem with Integers（区间求和区间修改（同加同减））
HDU 敌兵布阵（见树状数组）
HDU just a hook（区间求和区间修改（同时变成一个值））
vijos 小白逛公园（经典。十足的经典。导致我调了一整天。（点修改，区间查询））
代码放几个：
A Simple Problem with Integers//这个是我当时非常逗比的线段树

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <queue>
#include <stack>
#include <iomanip>
using namespace std;
int n,q;
struct Tree{
    int lt,rt;
    long long lazy;
    long long sum;
}tree[500005];
int w[100005];
void pushup(int root){
    tree[root].sum=tree[2*root].sum+tree[2*root+1].sum;
}
void build(int root,int begin,int end){
    tree[root].lt=begin;
    tree[root].rt=end;
    tree[root].lazy=0;
    if(begin==end)tree[root].sum=w[begin];
    else {
        build(2*root,begin,begin+((end-begin)>>1));
        build(2*root+1,begin+((end-begin)>>1)+1,end);
        pushup(root);
    }
}
void pushdown(int root){
    if(tree[root].lt==tree[root].rt){
        tree[root].sum+=tree[root].lazy;    
        return;
    }
    tree[2*root].lazy+=tree[root].lazy;
    tree[2*root+1].lazy+=tree[root].lazy;
     tree[2*root].sum+=(tree[2*root].rt-tree[2*root].lt+1)*1ll*tree[root].lazy;
    tree[2*root+1].sum+=(tree[2*root+1].rt-tree[2*root+1].lt+1)*1ll*tree[root].lazy;
    tree[root].lazy=0;
}
void modify(int root,int begin,int end,int modi){
    if(tree[root].lt>end||tree[root].rt<begin)return; 
    if(begin<=tree[root].lt&&tree[root].rt<=end){
        tree[root].lazy+=modi;
        tree[root].sum+=(tree[root].rt-tree[root].lt+1)*modi;
        return; 
    }
    pushdown(root);
    int mid=tree[root].lt+((tree[root].rt-tree[root].lt)>>1);
    if(mid>=begin)modify(root*2,begin,end,modi);
    if(mid<end)modify(root*2+1,begin,end,modi);
    pushup(root);
}
long long query(int root,int begin,int end){    
    if(tree[root].rt<begin||tree[root].lt>end)return 0; 
    if(tree[root].lt>=begin&&tree[root].rt<=end)return tree[root].sum;
    pushdown(root);
    long long ans=0;
    int mid=tree[root].lt+((tree[root].rt-tree[root].lt)>>1);
    if(begin<=mid)ans+=query(2*root,begin,end);
    if(mid<end)ans+=query(2*root+1,begin,end);
    return ans;
}
int main (){
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)scanf("%d",&w[i]);
    build(1,1,n);
    for(int i=1;i<=q;i++){
        char c;
        cin>>c;
        if(c=='Q')
        {
            int begin,end;
            scanf("%d%d",&begin,&end);
            printf("%lld\n",query(1,begin,end));
        }
        else {
            int begin,end,modi;
            scanf("%d%d%d",&begin,&end,&modi);
            modify(1,begin,end,modi);
        }
    }
    return 0;
}

小白逛公园：//表达了当时我愤怒的心理

/* 小白是什么？ 是狗啊！ 为什么要提到小白是狗这个事实呢？ 因为AC的过程之艰辛堪称日狗啊！ 首先样例是很弱的。 然后还有各种各样的坑点： 1.swap(a,b); 2.Struct的return 值。 样例只要变成这个！ 5 3 1 2 -3 4 5 1 6 7 2 2 -1 1 2 3 立即AC！ 所以说拥有一颗日狗的心是多么的重要！ --来自vijos客户端：小白逛你妹的公园！ --愤怒的张某某 考点：线段树询问之返回struct！ */
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
#include <ctime>
#define rd(i,x,n) for(int i=x;i<=n;i++)
#define mt(a,b) memset(a,b,sizeof(a))
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
using namespace std;
struct Tree{
    int sum;
    int sl,sr,maxn;
}t[2000005];
int m,n;
int w[500005];
void pushup(int rt){
    t[rt].sum=t[rt<<1].sum+t[rt<<1|1].sum;
    t[rt].sl=max(t[rt<<1].sl,t[rt<<1|1].sl+t[rt<<1].sum);
    t[rt].sr=max(t[rt<<1|1].sr,t[rt<<1].sr+t[rt<<1|1].sum);
    t[rt].maxn=max(max(t[rt<<1].maxn,t[rt<<1|1].maxn),t[rt<<1].sr+t[rt<<1|1].sl);
    return;
}
void build(int rt,int l,int r){
    if(l==r){
        t[rt].sum=t[rt].maxn=t[rt].sl=t[rt].sr=w[l];
        return;
    }
    int mid=(l+r)>>1;
    build(lson);
    build(rson);
    pushup(rt);
}
void modify(int rt,int l,int r,int s,int modi){
    if(l==r){
        t[rt].sum=t[rt].maxn=t[rt].sl=t[rt].sr=modi;
        return;
    }
    int mid=(l+r)>>1;
    if(s<=mid)modify(lson,s,modi);
    else modify(rson,s,modi);
    pushup(rt);
}
Tree query(int rt,int l,int r,int Ql,int Qr){
    if(l>=Ql&&r<=Qr)return t[rt];
    if(!(l>Qr||r<Ql)){
        int mid=(l+r)>>1;
        Tree x1,x2,tx;
        bool f=0,g=0;
        if(mid>=Ql){
            x1=query(lson,Ql,Qr);
            f=1;
        }
        if(mid<Qr){
            x2=query(rson,Ql,Qr);
            g=1;
        }
        if(f){
            if(g){
                tx.sum=x1.sum+x2.sum;
                tx.sl=max(x1.sl,x1.sum+x2.sl);
                tx.sr=max(x2.sr,x2.sum+x1.sr);
                tx.maxn=max(max(x1.maxn,x2.maxn),x1.sr+x2.sl);
                return tx;
            }
            return x1;
        }
        return x2;
    }
    else return t[0];
}
int main (){
    scanf("%d%d",&n,&m);
    rd(i,1,n)
        scanf("%d",&w[i]);
    build(1,1,n);
    rd(i,1,m){
        int order;
        scanf("%d",&order);
        if(order&1){
            int Ql,Qr;
            scanf("%d%d",&Ql,&Qr);
            if(Ql>Qr)swap(Ql,Qr);
            printf("%d\n",query(1,1,n,Ql,Qr).maxn);
        }
        else {
            int s,modi;
            scanf("%d%d",&s,&modi);
            modify(1,1,n,s,modi);
        }
    }
    return 0;
}

Just a Hook :真真正正的水题一枚

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <queue>
#include <stack>
#include <iomanip>
using namespace std;
int sum[500005],lz[500005];
void pushdown(int rt,int m){
    if(lz[rt])
    {
        lz[rt<<1]=lz[rt<<1|1]=lz[rt];
        sum[rt<<1]=lz[rt]*(m-(m>>1));
        sum[rt<<1|1]=lz[rt]*(m>>1);
        lz[rt]=0;
    }
}
void pushup(int rt){
    sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
void build(int rt,int l,int r){
    lz[rt]=0;
    sum[rt]=1;
    if(l==r)return;
    int mid=l+((r-l)>>1);
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
    pushup(rt);
}
void modify(int rt,int modi,int l,int r,int L,int R){
    if(L>r||R<l)return;
    if(L>=l&&R<=r)
    {
        lz[rt]=modi;
        sum[rt]=modi*(R-L+1);
        return;     
    }
    pushdown(rt,R-L+1);
    int mid=L+((R-L)>>1);
    if(l<=mid)modify(rt<<1,modi,l,r,L,mid);
    if(r>mid)modify(rt<<1|1,modi,l,r,mid+1,R);
    pushup(rt);
}
int main (){
    int n,cg;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int lenth,cg;
        scanf("%d%d",&lenth,&cg);
        build(1,1,lenth);
        while(cg--){
            int l,r,modi;
            scanf("%d%d%d",&l,&r,&modi);
            modify(1,modi,l,r,1,lenth);
        }
        printf("Case %d: The total value of the hook is %d.\n",i,sum[1]);
    }       
    return 0;
}

至此，lazy_tag和点修改线段树分析完毕！