RBF神经网络中bewrb()与newrbe()的区别

1.newrb()

该函数可以用来设计一个近似径向基网络。他的调用格式是[net,tr]=newrb(P,T,GOAL,SPRED,MN,DF)

其中P为输入向量，T为输出向量，GOAL为均方误差的目标，SPREED为径向基的扩展速度。返回值是一个构建好的网络

用newrb()创建的 RBF网络是一个不断的尝试过程，在创建中不断的增加中间层的数量和神经元的数目，知道满足输出的误差为止。

2.newrbe()

该函数设计一个严格的径向基网络，其调用格式是net=newrbe(P,T,SPEARD)，参数说明如上。

 

他们的区别就是在训练过程中newrb会多一个不断的寻找尝试的过程，如图所示：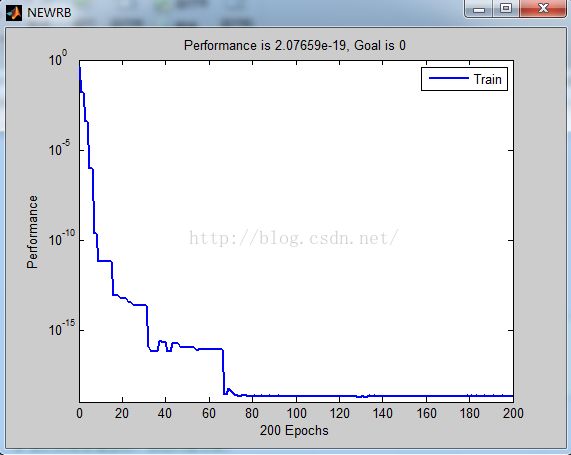

这幅图表示的就是在不断地 尝试中间层的节点数，来找到符合方差要求的值：

NEWRB, neurons = 0, MSE = 0.456005
NEWRB, neurons = 50, MSE = 1.01069e-16
NEWRB, neurons = 100, MSE = 1.97069e-19
NEWRB, neurons = 150, MSE = 2.05602e-19
NEWRB, neurons = 200, MSE = 2.07659e-19
NEWRB, neurons = 250, MSE = 2.07999e-19
NEWRB, neurons = 300, MSE = 4.32396e-17

这是寻找过程中自动打印的参数

 

 

------------------------------------------------------------------------

%% 清空环境变量
clc
clear

%% 产生输入 输出数据 
% 设置步长 
interval=0.01;

% 产生x1 x2
x1=-1.5:interval:1.5;   %       1*301
%x2=-1.5:interval:1.5;   %       1*301

% 按照函数先求得相应的函数值，作为网络的输出。
%F =20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); 
F =x1.^2-2; 
%% 网络建立和训练
% 网络建立 输入为[x1;x2],输出为F。Spread使用默认。
net=newrb(x1,F) ;    %输入[x1;x2]是2*301,F是1*301
%net=newrbe(x1,F) ; 
%% 网络的效果验证

% 我们将原数据回带，测试网络效果：
ty=sim(net,x1);

% 我们使用图像来看网络对非线性函数的拟合效果
figure
plot(x1,F,'rd');
hold on;
plot(x1,ty,'b-.');

title('可视化的方法观察准确RBF神经网络的拟合效果')
xlabel('x1')
ylabel('y')

grid on 

这是以y=x^2-2为测试函数的结果，读者可以将训练函数注释掉来自行比较过程